Exercícios de Atrito Cinético - Lista de Exercícios Resolvida
Questão 1
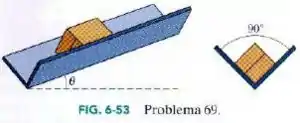
Na Fig. 6-53, um caixote escorrega para baixo em uma vala cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é . Qual é a aceleração do caixote em termos de , e ?
Questão 2
Uma pessoa empurra horizontalmente um caixote de com uma força de para deslocá-lo em um piso plano. O coeficiente de atrito cinético é . (a) Qual é o módulo da força de atrito? (b) Qual é o módulo da aceleração do caixote?
Ver solução completaQuestão 3
Um bloco de peso está deslizando para baixo em um plano inclinado de com a horizontal. Existe atrito entre o bloco e o plano. A aceleração do bloco é de dirigida para baixo ao longo do plano.
a) Desenhe o diagrama de corpo livre para o bloco durante a descida.
b) Calcule o valor do coeficiente de atrito cinético entre o bloco e o plano.
Ver solução completaQuestão 4
Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo. O coeficiente de atrito entre os blocos e o solo é 0,2.

Desenhe um diagrama das forças que atuam em cada um dos blocos e as escreva em um referencial determinado por você.
Determine a aceleração do conjunto e as forças que atuam em cada bloco.
Se a posição dos blocos fosse trocada o que mudaria nas forças e na aceleração?
Ver solução completaQuestão 5
Os blocos , e são dispostos como indicado na figura abaixo e ligados por cordas de massas desprezíveis. A massa de e de são iguais a . O coeficiente de atrito cinético entre cada bloco e a superfície é igual a . O bloco desce com velocidade constante. a) Desenhe dois diagramas de corpo livre separados mostrando as forças que atuam sobre e sobre . b) Ache a tensão na corda que liga o bloco e . c) Qual é o peso do bloco ?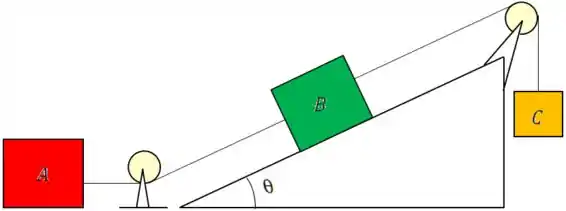
Questão 6
Considere a situação ilustrada abaixo onde os dois blocos estão ligados por uma corda que passa por uma polia. O bloco 1 tem massa e o bloco 2 tem massa . As massas da polia e da corda podem ser consideradas como sendo desprezíveis. Existe atrito em todas as superfícies e o coeficiente de atrito cinético é igual a 0,40. Uma força é aplicada no bloco 1 de tal forma que os blocos se deslocam com velocidade constante, o bloco 1 para à direita e o bloco 2 para à esquerda.
a) Faça o diagrama de corpo livre para o sistema e indique nos dois blocos, se existirem, as forças que formam pares ação-reação.
b) Escreva, na forma literal, as equações de movimento para o sistema. Resolva o sistema de equações e substitua os valores do enunciado para encontrar o vetor força . Utilize o sistema de coordenadas indicado.
Ver solução completaQuestão 7
Dois blocos de massas e estão em contato entre si, com o bloco sobre o bloco . Um fio ideal ligado ao bloco tem sua outra extremidade presa em um suporte vertical fixo. O bloco encontra-se inicialmente em repouso sobre uma superfície horizontal sem atrito, e num dado instante é puxado por uma forca horizontal constante, como mostra a figura. A força tem módulo suficiente para deslocar o bloco . Sabe-se que existe atrito entre as superfícies de contato entre os blocos, cujo coeficiente de atrito cinético é .
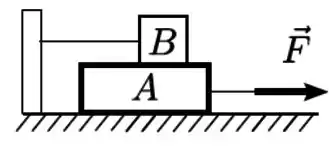
Considere que: o fio permanece esticado durante todo o tempo; a resistência do ar é desprezível; a gravidade tem módulo conhecido.
a) Faça o diagrama das forças que atuam sobre os blocos e separadamente;
b) Determine a aceleração com que o bloco se move e o módulo da tração que age no fio preso ao bloco ;
c) Determine o módulo da força resultante que o bloco exerce sobre o bloco .
Ver solução completaQuestão 8
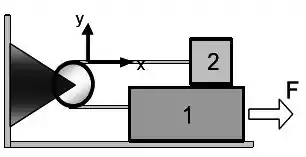
Um bloco de massa está sob a ação de uma força horizontal constante sobre uma superficie horizontal sem atrito. Sobre ele há um bloco de massa , preso à esquerda por um fio ideal. Este fio passa por uma roldana ideal que encontra-se fixa a uma parede vertical, e o conecta ao bloco de massa . Os segmentos do fio são paralelos ao plano horizontal; vide a figura abaixo. Suponha que haja atrito entre os blocos em contato entre si. Considere como conhecidos os valores dos coeficientes de atrito estático e cinético , as massas e e o módulo da aceleração da gravidade .
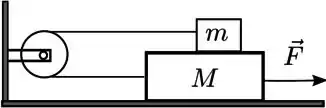
- Isole os blocos e represente por meio de um diagrama de corpo livre todas as forças que atuam em cada um deles.
- Suponha inicialmente que os blocos estejam em repouso. Determine o valor máximo do módulo de , para que o sistema permaneça em repouso.
- Considere agora que , cujo módulo é igual a , seja capaz de colocar os blocos em movimento com aceleração constante. Para o intervalo de tempo no qual os blocos permanecem em contanto entre si, determine os vetores aceleração de cada bloco em função de , , , e .
- Determine o módulo da tração do fio, para o caso do item anterior c)
Questão 9
Na figura abaixo, as massas dos blocos 2 e 3 são e , respectivamente. O coeficiente de atrito cinético entre o bloco 2 e a mesa é 0,10 enquanto o coeficiente de atrito estático é 0,20. Despreze o atrito entre os blocos 1 e 2.
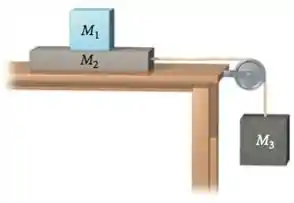
a) Usando a 3a Lei de Newton, faça o diagrama do corpo livre para cada um dos três blocos, indicando todos os pares de ação e reação.
b) Qual deve ser o valor mínimo da massa do bloco 1 para que o bloco 2 não se mova?
c) Calcule a aceleração do sistema se o bloco 1 é levantado.
d) Esboce os gráficos da velocidade e da posição do bloco 2, desde o momento em que o bloco 1 é levantado até após este momento.
Ver solução completaQuestão 10
Considere o sistema da figura abaixo. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito entre o bloco e a superfície é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa parado sobre o de baixo, se o de baixo estiver parado. Uma força é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma que o bloco de cima não desliza sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a SUBIR sobre o de baixo). Dê suas respostas em termos de e .
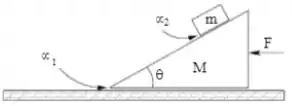
2) calcule o valor da normal entre os blocos nessa situação
Ver solução completaQuestão 11
(Cap 6 – Ex 27) Dois blocos, com e de peso, estão ligados por uma corda sem massa e deslizam para baixo em um plano inclinado de . O coeficiente de atrito cinético entre o bloco mais leve e o plano é e o coeficiente de atrito cinético entre o bloco mais pesado e o plano é . Supondo que o bloco mais leve desce na frente, determine (a) o módulo da aceleração dos blocos e (b) a tensão da corda.
Ver solução completaQuestão 12
Considere o sistema da figura abaixo. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito entre o bloco e a superfície é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa parado sobre o de baixo, se o de baixo estiver parado. Uma força é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma que o bloco de cima não desliza sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a SUBIR sobre o de baixo). Dê suas respostas em termos de e .
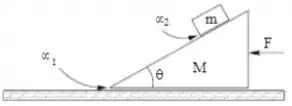
- Faça o diagrama de forças nos dois blocos, enquanto há movimento, mas o de cima não se move sobre o de baixo. Marque quais dessas forças são pares de ação e reação. Faça outro desenho e separe os blocos para maior clareza.
Questão 13
Um bloco de é puxado por uma corda que faz com a horizontal. Quando a tração na corda é de , o bloco desliza a uma velocidade constante. O coeficiente de atrito entre o bloco e o chão vale aproximadamente (utilize se necessário ):
- 0,10
- 0,19
- 0,31
- 0,43
- 0,57
Questão 14
Um bloco de massa está apoiado sobre o lado esquerdo de um bloco de massa . O coeficiente de atrito cinético entre os dois blocos é de 0,3 e a superfície sobre a qual o bloco de está apoiado é sem atrito. Uma força horizontal constante de módulo é aplicada ao bloco de , colocando-o em movimento como mostrado na figura abaixo. Se a distância que a superfície frontal do bloco menor percorre sobre o bloco maior é de .
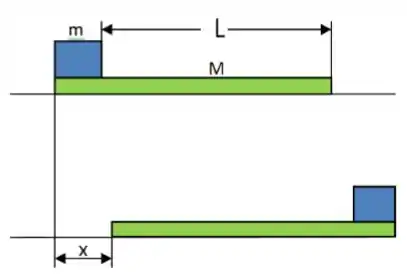
a) Desenhe todas as forças que atuam no sistema
b) Calcule a aceleração do bloco menor em relação ao solo
c) Calcule a aceleração do bloco maior em relação ao solo
d) Qual a distância percorrida pelo bloco maior e quanto tempo o bloco menor levará até chegar ao lado direito do bloco maior?
Ver solução completaQuestão 15
Um bloco de massa desliza sobre um plano inclinado que faz um ângulo com a horizontal. O plano tem uma superfície rugosa, cujo coeficiente de atrito cinético, , é igual a 0,2. O bloco localiza-se inicialmente no topo do plano, a uma altura com a horizontal, e inicia seu movimento a partir do repouso. O plano está montado sobre uma mesa de altura . Ao final do deslizamento ao longo do plano, o bloco cai sob ação da força peso e de uma força de resistência do ar. Veja a figura ao lado para um esquema da situação (use ).
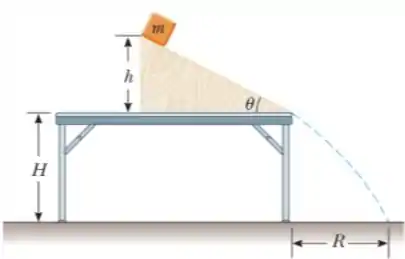
(a) Determine o diagrama de corpo livre (diagrama de forças) para o bloco quando o mesmo inicia seu movimento no topo do plano e outro diagrama para o bloco após o mesmo perder contato com o plano.
(b) Para cada força indicada nestes diagramas, aponte o devido par ação e reação (terceira Lei de Newton) da mesma e discuta seu efeito (escreva no máximo até duas linhas para cada força).
(c) Determine o vetor velocidade do bloco quando o mesmo atinge o final do plano inclinado. Escreva sua resposta na forma .
(d) Ignore a resistência do ar e determine o alcance do bloco. Dica geral: faça substituições numéricas apenas na etapa final das soluções dos itens (c) e (d). Para o item (d), caso você não tenha feito o item (c), deixe a resposta em termos de e .
Ver solução completaQuestão 16
Considere a situação ilustrada abaixo onde os dois blocos estão ligados por uma corda que passa por uma polia. O bloco 1 tem massa e o bloco 2 tem massa . As massas da polia e da corda podem ser consideradas como sendo desprezíveis. Existe atrito em todas as superfícies e o coeficiente de atrito cinético é igual a 0,40. Uma força é aplicada no bloco 1 de tal forma que os blocos se deslocam com velocidade constante, o bloco 1 para à direita e o bloco 2 para à esquerda.
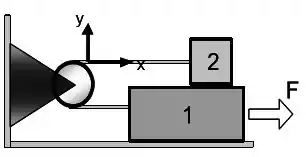
a) Faça o diagrama de corpo livre para o sistema e indique nos dois blocos, se existirem, as forças que formam pares ação-reação.
b) Escreva, na forma literal, as equações de movimento para o sistema. Resolva o sistema de equações e substitua os valores do enunciado para encontrar o vetor força . Utilize o sistema de coordenadas indicado.
Ver solução completaQuestão 17
Três blocos de massa , e estão conectados por cordas ideais através de uma polia ideal, apoiados em superfícies inclinadas de ângulos e como mostrado na figura. As massas dos blocos valem , , , , , e . Os valores dos coeficientes de atrito estático e cinético entre o bloco 1 e seu plano inclinado são respectivamente e .
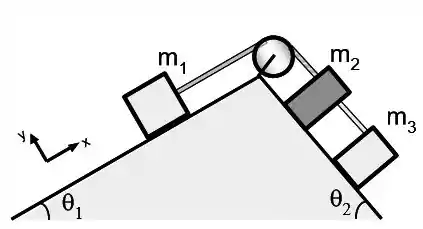
a) Faça um diagrama de corpo livre de cada bloco no espaço abaixo. Usando as leis de Newton, determine o valor da força de atrito estático sobre o bloco 1 para que o sistema permaneça em repouso. Não existe atrito entre os blocos 2 e 3 e o plano inclinado no qual estão apoiados.
b) Considere agora que o bloco 3 sofra a ação de uma força para baixo paralela ao plano inclinado que põe o sistema em movimento. Após certo momento, a ação dessa força cessa. Nesse instante o sistema de blocos está descendo o plano inclinado com velocidade de módulo . A partir desse instante obtenha o valor da aceleração do bloco 1.
c) Calcule a força de tração da corda sobre o bloco 1 durante a aceleração do ítem ().
Ver solução completaQuestão 18
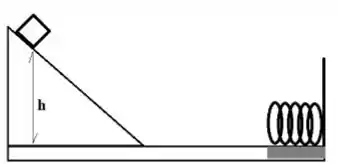
1b) Na figura, um bloco de cai a partir do repouso de uma altura , e desliza num plano inclinado e numa pista sem atrito até bater numa mola relaxada . Na região onde a mola se encontra, existe atrito cinético entre o bloco e o solo . Nestas condições, calcule a compressão máxima da mola.
Questão 19

É permitido o uso de calculador científica simples.
Na figura abaixo, a polia de raio e massa desprezível, gira no sentido horário enrolando um cordão ligado a um bloco. O bloco, por sua vez, está ligado a uma mola ideal que tem sua outra extremidade fixa. A polia gira até que a mola sofra uma deformação de , quando então o sistema entra em repouso. A seguir, a polia é liberada. O atrito no eixo da polia é desprezível, mas há atrito entre o bloco e a superfície de apoio. Despreze a massa do cordão e admita que ele não deslize. Use: massa do bloco ; coeficiente de atrito cinético entre o bloco e a superfície ; constante elástica da mola .
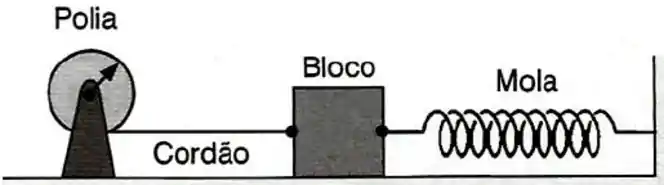
a) Determine a energia mecânica total do sistema quando ele estiver em repouso imediatamente antes da polia ser liberada.
b) Determine a velocidade escalar do bloco quando ele passar pela posição em que a mola está relaxada.
c) Suponha que o bloco andou depois de passar pela posição de relaxamento da mola até entrar em repouso momentaneamente. Determine o deslocamento angular da polia desde que ela foi liberada até este instante.
Ver solução completaQuestão 20
Na figura, o fio e a roldana são ideais, e o plano fixo em que se apoia o bloco possui inclinação com a horizontal. Em todas as situações abaixo, o fio permanece tensionado e , mas o bloco pode variar. Quando necessário substituir valores, use .
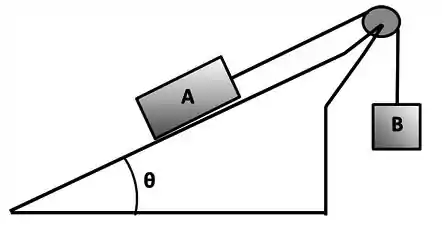
Neste item, considere e . Se o bloco adquire aceleração para baixo de , calcule o coeficiente de atrito cinético entre o plano e o bloco .
Ver solução completaQuestão 21
Um jardineiro empurra um cortador de grama através de trecho de grama horizontal com uma velocidade constante através da aplicação de uma força As setas no diagrama indicam corretamente as suas direções, mas não necessariamente as magnitudes das demais forças agindo sobre o cortador de grama: a normal , o peso e a força de atrito Qual das seguintes relações entre as magnitudes das diferentes forças é a correta?
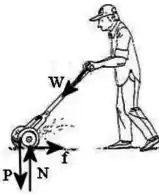
- Nenhuma das anteriores.
Questão 22
Dois blocos de massas e estão ligados por um fio de massa desprezível e repousam sobre um plano inclinado que forma um ângulo com a direção horizontal. O bloco é empurrado por uma força constante de módulo que faz um ângulo com a direção do plano inclinado, (veja a figura) e o conjunto entra em movimento. O coeficiente de atrito cinético entre os blocos e a superfície do plano inclinado é . Todas as respostas devem ser fornecidas em relação ao sistema de coordenadas mostrado na figura.
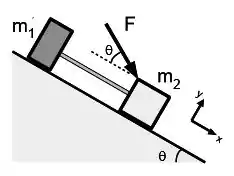
(a) Faça o diagrama do corpo livre, indicando claramente todas as forças que agem em cada um dos blocos. Indique as forças que formam par ação e reação.
(b) Escreva as equações do movimento na sua forma literal em termos das componentes das forças que agem sobre os blocos. Informe as expressões literais para as componentes da força e dos pesos dos blocos e .
Considere para os itens seguintes os seguintes valores: ; ; ; ; ; ; .
(c) Determine os módulos da aceleração dos blocos e da tensão no fio que liga os blocos.
(d) Considere agora que o sistema esteja na condição de repouso. Para que ele mantenha esta condição inercial, determine o menor valor do coeficiente de atrito estático entre os blocos e a superfície de apoio.
Ver solução completaQuestão 23
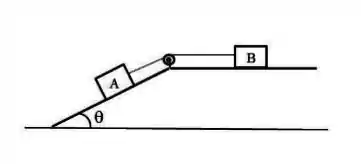
Dois corpos estão ligados por um fio que passa por uma polia conforme mostrado na figura. O suporte tem uma face inclinada e outra horizontal. O corpo desce sobre a face inclinada enquanto o corpo se move sobre a face horizontal (sem chegar até a polia). A superfície sobre a qual estão os corpos se caracteriza por um coeficiente de atrito estático e um coeficiente de atrito cinético . Considere fio e polia ideais. Assuma . Aproxime . Você pode dar o resultado aproximado com uma casa decimal.
LEMBRETE: Todos os seus passos devem ser explicitados de forma clara.
(a) Faça um diagrama das forças do sistema.
(b) Sendo as massas dos corpos e , respectivamente, e , calcule a tração no fio.
(c) Para a mesma situação do item anterior, calcule a aceleração dos dois corpos.
Questão 24
[Enunciado comum às Questões 3 e 4]
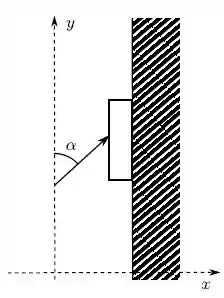
Uma força atua horizontalmente sobre um bloco de massa e que se encontra apoiado em uma parede vertical, como mostrado na figura. O coeficiente de atrito estático entre o bloco e a parede é . Considere o módulo da aceleração gravitacional no local .
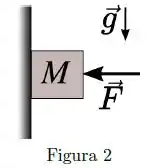
[Questão 4]
Para uma força aplicada de módulo , o bloco desce com aceleração de módulo . O coeficiente de atrito cinético entre o bloco e a parede é igual a:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 25
Parte I - Considere a figura mostrada nessa questão e forneça suas respostas em notação científica no sistema internacional de unidades considerando rigorosamente o conceito de algarismos significativos. A corda e a roldana são considerados ideais.
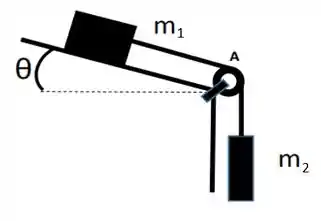
Dados:
Determine:
a) O menor valor para o coeficiente de atrito estático na rampa inclinada que mantém o sistema em repouso.
b) O módulo da aceleração do sistema para e o valor da tensão na corda, se o sistema sofre um pequeno impulso que o põe em movimento.
Ver solução completaQuestão 26
Parte III:
Uma força atua sobre o bloco conforme a figura ao lado, produzindo o movimento dos blocos , e juntos sobre uma superfície áspera com coeficiente de atrito cinético . As massas desses blocos são respectivamente, e .
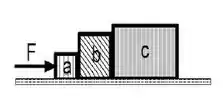
(e) Determine a força que o bloco faz sobre o .
1-( )
2-( )
3-( )
4-( )
5-( )
Ver solução completaQuestão 27
Considere que um bloco de massa desce o plano inclinado da Figura 2.
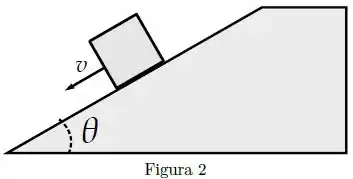
Se os coeficientes de atrito estático e cinético entre o bloco e o planos são respectivamente e , qual o módulo da força de atrito que atua sobre o bloco? Dados: , , .
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 28
Um bloco de madeira de massa é puxado com velocidade constante por uma força de magnitude , cuja direção faz um ângulo com a horizontal. A magnitude da força de atrito sofrida pelo bloco é:
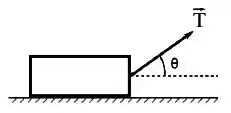
(a) Igual à da força peso.
(b)
(c)
(d) Não é possível determinar sem conhecer o coeficiente de atrito cinético.
(e) Não é possível determinar sem conhecer o coeficiente de atrito estático.
Ver solução completaQuestão 29
Um bloco de massa é puxado com a ajuda de uma corda por uma superfície rugosa, com o coeficiente de atrito cinético , como demonstra a figura abaixo. Sabe-se que o ângulo da tração com a horizontal é .
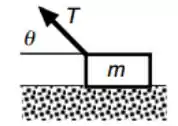
Qual é a melhor representação para a força de atrito, sabendo que a aceleração é constante e diferente de zero?
a)
b)
c)
d)
e) Nenhuma das anteriores
Ver solução completaQuestão 30
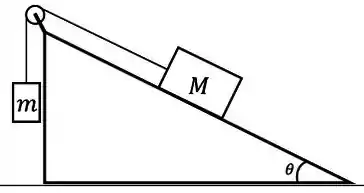
Considere a situação ilustrada na figura abaixo. Um bloco de massa está conectado através de fios e polias ideais a um segundo bloco de massa . O bloco de massa desliza com atrito sobre uma superfície inclinada de um ângulo com a horizontal enquanto o bloco de massa desce verticalmente com velocidade constante. Responda as perguntas a seguir: (Lembre-se que sua resposta deve ser dada em função dos dados fornecidos no problema: , , , )
a) Faça o diagrama das forças que atuam sobre cada um dos blocos.
b) Determine o módulo da força de atrito entre o bloco de massa M e o plano inclinado;
c) Encontre o coeficiente de atrito cinético entre o bloco de massa M e o plano inclinado.
Questão 31
Considere o sistema de corpos 1 e 2, presos a fios ideais que passam por polias ideais, dado pela figura. Admita como dadas as seguintes grandezas: massas dos dois corpos, coeficientes de atrito cinético () e estático () entre o corpo 2 e plano inclinado, ângulo de inclinação () do plano inclinado em relação à horizontal, aceleração da gravidade local () e o fato do sistema estar inicialmente em repouso.
Obs.: todas as soluções devem partir explicitamente de leis físicas adequadas e possuir desenvolvimento literal.
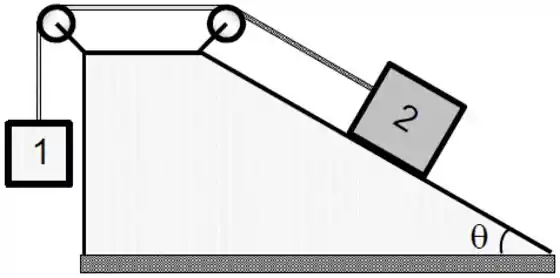
a) O corpo 1 tem massa e o corpo 2 tem massa . O sistema está em equilíbrio estático, na iminência do corpo 2 descer. Faça um diagrama de corpo livre para o corpo 2 nesta situação.
b) Aplique a 2ª Lei de Newton e escreva as equações que relacionam as forças com a aceleração para os dois corpos.
c) Determine a razão entre e para esta situação.
d) Considere agora que o corpo 1 tenha sua massa alterada para , de forma que o corpo 2 sobe o plano inclinado. Faça um diagrama de corpo livre para o corpo 2 nesta situação.
e) Encontre uma expressão literal para o valor da aceleração dos dois corpos.
Ver solução completaQuestão 32
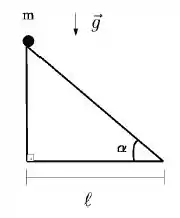
Um corpo de massa desliza do topo de uma rampa cuja base tem comprimento , conforme a figura abaixo. O coeficiente de atrito dinâmico entre o corpo e a superfície da rampa é . Qual deverá ser a relação satisfeita pelo ângulo () para que o tempo de deslizamento do corpo ao longo de toda rampa seja o maior possível?
Obs: Mínimos e máximos de uma função são caracterizados pelo fato de que a derivada da função se anula em tais pontos.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 33
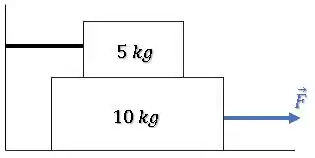
Um bloco de é colocado sobre um de , conforme a figura. Uma força horizontal de é aplicada ao bloco de e o bloco de está preso à parede por uma corda sem massa. O coeficiente de atrito cinético entre todas as superfícies é . A tração na corda é:
A.
B.
C.
D.
E.
Ver solução completaQuestão 35
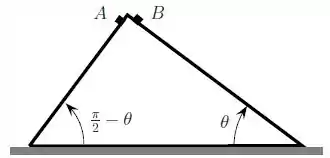
Considere duas rampas inclinadas, perpendiculares entre si, e que formam com o solo um triângulo retângulo, como ilustra a figura. Dois blocos e de mesma massa m estão, inicialmente, em repouso nos pontos mais altos de cada rampa. O bloco encontra-se sobre a rampa menos inclinada, a da direita na figura, que forma um ângulo com a horizontal e, nela, o atrito é desprezível. Em contrapartida, o coeficiente de atrito cinético entre a rampa da esquerda e o bloco , que desliza sobre ela é . Verifica-se, então, que os blocos deslizam sobre as rampas.
a) Supondo que ambos os blocos iniciem seus movimentos de descida no mesmo instante e que atinjam o solo simultaneamente, determine o coeficiente de atrito . Sua resposta deve ser dada em termos das grandezas: , e .
b) Discuta o resultado do item anterior para .
Questão 36
Um cachorro pode arrastar suas caixas A e B, ligadas por uma corda, sobre uma suprerfície horizontal de neve. Os coeficientes de atrito estático e cinético entre as caizas e a neve são respectivamente iguais a e . Considere as cordas de massa desprezível e não extensíveis (ideais).

- Faça o diagrama de corpo livre de cada caixa;
- Qual é a força de atrito estático máxima sobre cada caixa;
- Qual é a força mínima que o cachorro precisa aplicar à corda que o prende à caixa A para iniciar o movimento das caixas;
- Em movimento, se a tração na corda entre as caixas A e B vale 99N, qual é a aceleração da caixa A e a tração na corda que prende a caixa A ao cachorro.
Questão 37
Um bloco A, de massa , desce um plano inclinado de ângulo com uma velocidade constante enquanto uma placa B, de massa , está parada sobre o bloco A; esta placa está presa a uma parede no topo do plano inclinado. Assuma que o coeficiente de atrito é o mesmo entre todas as superfícies.
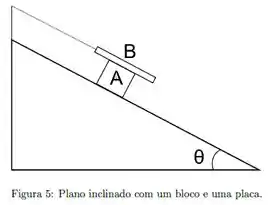
(a) Desenhe o diagrama de forças que agem separadamente nos blocos A e B nas figuras abaixo.
(b) Quais são os pares de forças de ação e reação?
(c) Calcule a forca de atrito entre o bloco A e o bloco B.
(d) Calcule a tensão sobre a corda segurando a placa B.
(e) Calcule a força de atrito entre o bloco A e a superfície do plano inclinado,
(f) Derive o coeficiente de atrito em função das variáveis do problema. Ele depende das massas?
Ver solução completaQuestão 38
Questão 2) Os blocos e da figura ao lado tem massas e . Considere o fio inextensível, a polia sem atrito e as massas do fio e da polia desprezíveis. Os coeficientes de atrito estático e cinético entre o bloco e a mesa são e , respectivamente.
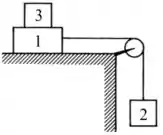
b) Determine a aceleração do bloco quando o bloco é removido subitamente de cima do bloco . Faça um diagrama de corpo livre para os blocos.
Ver solução completaQuestão 39
Um bloco de massa está apoiado sobre o lado esquerdo de um bloco de massa . O coeficiente de atrito cinético entre os dois blocos é de 0,3 e a superfície sobre a qual o bloco de está apoiado é sem atrito. Uma força horizontal constante de módulo é aplicada ao bloco de , colocando-o em movimento como mostrado na figura abaixo. Se a distância que a superfície frontal do bloco menor percorre sobre o bloco maior é de .
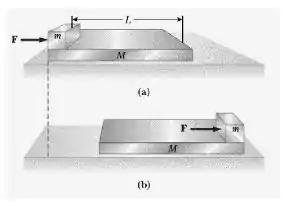
a) Quanto tempo levará até esse bloco chegar ao lado direito do bloco de , como mostrado na figura? (Observe: os dois blocos são colocados em movimento quando é aplicada.)
b) Qual a distância percorrida pelo bloco de nesse processo?
Ver solução completaQuestão 40
Um bloco está localizado em uma madeira plana e rugosa. É encontrado que quando o plano é inclinado de 30o com a horizontal, o bloco desliza para baixo com velocidade constante. O coeficiente de atrito cinético do bloco com o plano é:
Questão 41
Considere o sistema da figura abaixo. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito entre o bloco e a superfície é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa parado sobre o de baixo, se o de baixo estiver parado. Uma força é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma que o bloco de cima não desliza sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a SUBIR sobre o de baixo). Dê suas respostas em termos de e .
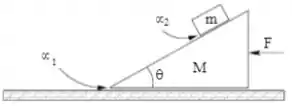
4) determine o valor máximo da força
Ver solução completaQuestão 42
Um bloco de madeira é arrastado com rapidez constante sobre uma chapa de aço áspera por uma força nas duas situações mostradas na figura. O módulo da força é o mesmo nas duas situações. O módulo da força de atrito em (ii) comparado com o módulo da força de atrito em (i) é:
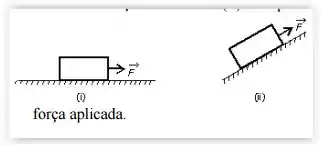
A) o mesmo
B) maior
C) menor
D) menor para alguns ângulos e maior para outros
E) pode ser maior ou menor, dependendo do modulo da força
Ver solução completaQuestão 43
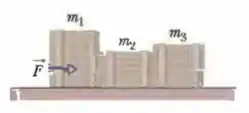
(Cap 6 – Ex 28) A Fig. 6-32 mostra três caixotes sendo empurrados sobre um piso de concreto por uma força horizontal de módulo . As massas dos caixotes são , e . O coeficiente de atrito cinético entre o piso e cada um dos caixotes é de . (a) Qual é o módulo da força exercida sobre o bloco pelo bloco ? (b) Se os caixotes deslizassem sobre um piso polido, com um coeficiente de atrito cinético menor que , o módulo seria maior, menor ou igual ao valor quando o coeficiente de atrito era ?
Questão 45
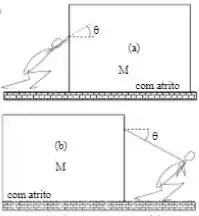
Uma pessoa tem que deslocar uma caixa de massa por um plano horizontal com atrito, conforme a figura. Em qual dessas situações ela fará força maior, (a) ou (b)?
Questão 46
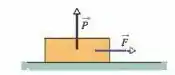
(Cap 6 – Ex 9 ) Um bloco de está inicialmente em repouso em uma superfície horizontal. Uma força horizontal de módulo e uma força verticalsão aplicadas ao bloco Os coeficientes de atrito entre o bloco e a superfície são e. Determine o módulo da força de atrito que age sobre o bloco se o módulo de é (a) (b) e (c)
Questão 47
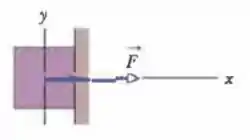
(Cap 6 – Ex 17) Uma força horizontal de empurra um bloco de de peso contra uma parede vertical (Fig. 6-26). O coeficiente de atrito estático entre a parede e o bloco é e o coeficiente de atrito cinético é . Suponha que o bloco não esteja se movendo inicialmente. (a) O bloco vai se mover? (b) Qual é a força que a parede exerce sobre o bloco em termos dos vetores unitários?
Questão 48
Um cubinho de gelo escorrega sobre um plano inclinado de inclinação no dobro do tempo que leva para escorregar em um plano análogo, mas sem atrito. Qual é o valor do coeficiente de atrito cinético entre o gelo e o plano?
Ver solução completaQuestão 49
(Cap 6 – Ex 7) Um bloco de é empurrado ao longo de um piso horizontal por uma força de módulo que faz um ângulo com a horizontal (Figura 6-19). O coeficiente de atrito cinético entre o bloco e o piso é . Calcule (a) o módulo da força de atrito que o piso exerce sobre o bloco e (b) o módulo da aceleração do bloco.
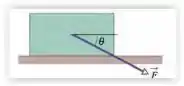
Questão 50
(Cap 6 – Ex 18) Um bloco de é empurrado sobre um piso por uma força horizontal constante de módulo . A Fig. 6-30 mostra a velocidade do bloco em função do tempo quando o bloco se desloca sobre o piso ao longo de um eixo . A escala vertical do gráfico é definida por . Qual é o coeficiente de atrito cinético entre o bloco e o piso?
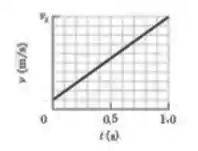
Questão 51
(Cap 6 – Ex 16) Você depõe como perito em um caso envolvendo um acidente no qual o carro bateu na traseira de um carro que estava parado em um sinal vermelho no meio de uma ladeira (Fig. 6-25). Você descobre que a inclinação da ladeira é , que os carros estavam separados por uma distância quando o motorista do carro freou bruscamente, bloqueando as rodas (o carro não dispunha de freios ABS), e que a velocidade do carro no momento em que o motorista pisou no freio era . Com que velocidade o carro bateu no carro se o coeficiente de atrito cinético era (a) 0,60 (estrada seca) e (b) (estrada coberta de folhas molhadas)

Questão 52
(Cap 6 – Ex 1) Uma cômoda com uma massa de , incluindo as gavetas e as roupas, está em repouso sobre o piso. (a) Se o coeficiente de atrito estático entre a cômoda e o piso é , qual é o módulo da menor força horizontal necessária para fazer a cômoda entrar em movimento? (b) Se as gavetas e as roupas, com uma massa total de , são removidas antes de empurrar a cômoda, qual é o novo módulo mínimo?
Ver solução completaQuestão 53
7. Um bloco de é posto em movimento com uma velocidade inicial de sobre uma superfície horizontal áspera. Se o bloco atinge o repouso s depois de entrar em movimento, qual é o coeficiente de atrito cinético entre o bloco e a superfície?
Questão 54
(Cap 6 – Ex 63) Na Fig. 6-54, o coeficiente de atrito cinético entre o bloco e o plano inclinado é e o ângulo . Quais são (a) o módulo e (b) o sentido (para cima ou para baixo ao longo do plano) da aceleração do bloco se ele está escorregando para baixo? Quais são (c) o módulo e (d) o sentido da aceleração se o bloco está escorregando para cima?
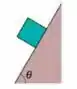
Questão 55
(Cap 6 – Ex 64) Na Fig. 6-50, o bloco 1, de massa , e o bloco 2, de massa , estão ligados por um fio de massa desprezível e são inicialmente mantidos em repouso. O bloco 2 está sobre uma superfície sem atrito com uma inclinação . O coeficiente de atrito cinético entre o bloco 1 e a superfície horizontal é . A polia tem massa e atrito desprezíveis. Ao serem liberados, os blocos entram em movimento. Qual é a tensão do fio?
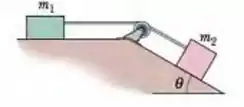
Questão 56
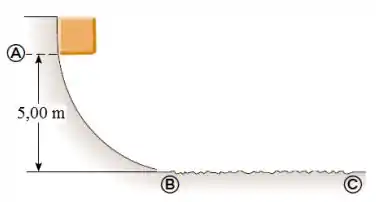
Um carrinho desliza, a partir do repouso, do alto de uma montanha russa de de altura, com atrito desprezível. Chegando ao sopé da montanha, ele é freado pelo terreno coberto de areia, parando em . Qual é o coeficiente de atrito cinético entre o carrinho e a areia?
Questão 57
Em um plano inclinado um bloco desliza para baixo sob a ação da gravidade a uma velocidade constante. É correto afirmar sobre a força de atrito entre a superfície do plano e o bloco:
a) Seu módulo é igual ao peso do bloco;
b) Seu módulo depende da velocidade do bloco;
c) Se aumentarmos o ângulo de inclinação do plano o movimento passa a ser acelerado;
d) Se diminuirmos o ângulo de inclinação do plano o bloco para instantaneamente;
e) o módulo da força de atrito é igual à diferença entre o peso e a normal agindo no bloco;
Ver solução completaQuestão 58
Um bloco de massa encontra-se sob um plano inclinado cuja superfície faz um ângulo com a horizontal. Nesta situação, o bloco encontra-se em repouso devido ao atrito estático com a superfície. A inclinação do plano é aumentada por um pequeno ângulo e o bloco começa a deslizar com aceleração de módulo igual a . Sobre os coeficientes de atrito cinético, , e estático, , para a força de atrito entre o bloco e a superfície do plano inclinado podemos afirmar:
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 59
Considere uma rampa, inclinada de um ângulo em relação à horizontal, no início da qual encontra-se um carrinho. Ele então recebe uma pancada que o faz subir até uma certa distância, durante o tempo , descendo em seguida até sua posição inicial. A “viagem” completa dura um tempo total . Sendo o coeficiente de atrito cinético entre o carrinho e a rampa, a relação é igual a
Ver solução completa
Questão 60
Um bloco de peso está deslizando para baixo em um plano inclinado de com a horizontal. Existe atrito entre o bloco e o plano. A aceleração do bloco é de dirigida para cima ao longo do plano.
a) Desenhe o diagrama de corpo livre para o bloco durante a descida.
b) Calcule o valor do coeficiente de atrito cinético entre o bloco e o plano.
Ver solução completaQuestão 61
Um automóvel de massa inicia em um piso horizontal, a partir do repouso, a subida de uma rampa, cuja altura vertical final é . Ao chegar ao topo da rampa sua energia cinética é igual a . Neste instante, um defeito de travamento das rodas ocorre e o automóvel inicia uma descida, deslizando por outra rampa, até chegar ao nível horizontal. Nesse deslizamento a perda para o meio externo é de de sua energia mecânica no topo. Ao chegar ao nível horizontal ainda com velocidade, o automóvel colide com uma mola horizontal estática comprimindo-a até parar. A mola possui constante elástica , estando com uma extremidade livre e outra presa em uma parede. Na região onde está a mola o piso é rugoso com coeficiente de atrito cinético .
Obs.: Em todos os itens abaixo explicite a razão pela qual é válida a lei física aplicada. Resolva primeiro literalmente. Somente depois faça a aplicação numérica quando for o caso. Considere .
Obtenha uma expressão, em função dos dados conhecidos, para o valor de energia gasto pelo automóvel durante a subida da rampa. Assuma de eficiência do motor. Calcule seu valor numérico.
Encontre uma expressão literal para o valor da velocidade do automóvel ao terminar a descida da rampa. Calcule seu valor numérico.
Deduza uma equação algébrica quadrática para a deformaçãoo máxima da mola em termos dos dados literais fornecidos ( e ).
Ver solução completaQuestão 62
Um bloco abandonado em repouso está descendo com velocidade constante a superfície de um plano inclinado. A força de atrito que a superfície exerce sobre o bloco é
- Paralela à superfície do plano incilinado com módulo menor que o peso do bloco;
- Perpendicular à superfície do plano inclinado com módulo menor do que o peso do bloco;
- Paralela à superfície do plano inclinado com módulo maior do que o peso do bloco;
- Perpendicular à superfície do plano inclinado com módulo maior do que o peso do bloco;
- Paralela à superfície do plano inclinado com módulo igual ao peso do bloco.
Questão 63
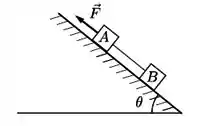
Dois blocos A e B de massas iguais a , são ligados entre si por um fio ideal e colocados, em repouso, sobre uma rampa inclinada de um ângulo em relação à horizontal. Os coeficientes de atrito cinético entre a superfície do plano inclinado e as superfícies do bloco A e do bloco B são, respectivamente, iguais a e . Num dado instante o bloco A é puxado por uma força de módulo constante, e paralela à superfície, de forma que ele passa a se deslocar superfície acima, como mostra a figura. A força tem módulo suficiente para manter os blocos em movimento e o fio esticado
- Isole os blocos e represente todas as forças que agem em cada bloco, separadamente, identificado-as;
- Determine o módulo da aceleração com que os blocos se movem;
- Determine o módulo da tração que age no fio que liga os blocos;
- Se trocarmos os blocos de posição, mantendo a mesma força aplicada sobre o bloco de cima, qual a diferença entre os novos valores de aceleração e tração em relação aos encontrados nos itens (b) e (c)? Justifique sua resposta.
Questão 65
[ENUNCIADO COMUM ÀS QUESTÕES 5 e 6]
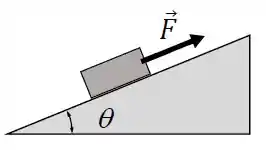
Um bloco de massa está em movimento ao longo da superfície de um plano inclinado que faz um ângulo com a horizontal e está submetido a uma força .
[QUESTÃO 6]
A massa do bloco é , a força aplicada tem módulo e o coeficiente de atrito cinético é . Considere , e . O módulo da força de atrito atuando sobre o bloco é
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 66
1. Um carro de massa sobe uma rampa que faz uma inclinação de com a
horizontal a uma velocidade de 20 m/s. Ao acionar subitamente os freios, passa a derrapar,
percorrendo uma distância de metros até parar. A força de atrito entre os pneus e o chão
vale:
zero
Ver solução completaQuestão 67
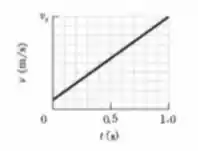
Um bloco de é empurrado sobre um piso por uma força horizontal constante de módulo . A figura abaixo mostra a velocidade do bloco em função do tempo quando o bloco se desloca sobre o piso ao longo de um eixo . A escala vertical do gráfico é definida por . Qual é o coeficiente de atrito cinético entre o bloco e o piso?
Questão 68
Parte II - Coloque V de verdadeiro ou F de falso na resposta correta. Justifique sua opção.
- Observe as situações da figura.
- Um bloco é puxado por uma força , transmitida por uma corda, com velocidade
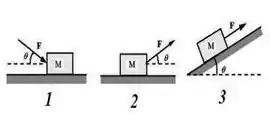
A força normal sobre o bloco M tem módulo igual a nas seguintes situações:
1-( ) somente em 1.
2-( ) somente em 2.
3-( ) em 1 e 2.
4-( ) em 2 e 3.
5-( ) em 1, 2, 3.
constante sobre uma superfície áspera. A corda faz um ângulo com a horizontal. A força de
atrito cinética entre o bloco e a superfície é . Marque qual das ações aumentará a força de
atrito sobre o bloco.
1-( ) aumentar o ângulo 𝜃 com a corda.
2-( ) aumentar a velocidade do bloco.
3-( ) diminuir a velocidade do bloco.
4-( ) aumentar a massa do bloco.
5-( ) diminuir a massa do bloco.
Ver solução completaQuestão 69
Parte I - Considere o sistema físico na figura abaixo.
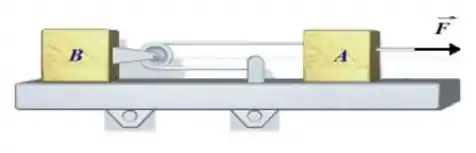
Os blocos possuem massas e . A roldana e os fios são ideais. Existe atrito entre o piso e os blocos A e B com coeficiente de atrito cinético . A força que puxa o bloco A tem valor . Devido à ligação entre os fios e a roldana, a aceleração do bloco B é duas vezes menor que a do bloco A.
- Faça os diagramas de forças dos blocos A, B e da roldana.
- Encontre o valor da aceleração do bloco A () e do bloco B ().
- Encontre o módulo da tensão e da força que a roldana faz sobre o bloco B
Questão 70
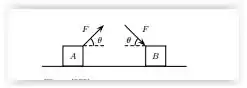
Dois blocos idênticos, A e B, de massa m, estão deslizando para a direita sobre um plano horizontal, sujeitos a forças de mesmo módulo F, como mostrado na figura, sendo o bloco A puxado e o bloco B empurrado. O coeficiente de atrito cinético µc é o mesmo entre os blocos e a superfície. Das afirmações que se seguem, assinale as CORRETAS:
- O módulo da força de atrito entre o bloco A e o plano é menor que o módulo da força de atrito entre o bloco B e o plano
- A aceleração dos blocos A e B em relação à Terra é a mesma
- A força normal que age no corpo A tem módulo
(a) apenas (I) e (III)
(b) apenas (I) e (II)
(c) apenas (III)
(d) apenas (I)
(e) apenas (II) e (III)
(f) apenas (II)
Ver solução completaQuestão 71
Um disco de raio e massa e um cubo de lado e mesma massa, estão no topo de um plano com comprimento inclinado de com a horizontal. Existe atrito entre o plano inclinado e os dois objetos, os coeficientes de atrito cinético e atrito estático são respectivamente e . Na base do plano existe um trilho na vertical com o formato de um anel de raio como ilustra o desenho. A base do plano e o trilho têm superfícies com atrito desprezível. Na saída do trilho, está em repouso um segundo cubo idêntico ao primeiro com seu centro de massa na posição . Logo após o segundo cubo, a superfície horizontal apresenta um coeficiente de atrito cinético variável e no final desta superfície está uma mola com constante elástica . A superfície embaixo da mola tem atrito desprezível. A origem do sistema de coordenadas coincide com o centro do anel. A aceleração da gravidade é . Desenvolva as equações na forma literal para somente no final substituir as variáveis pelos valores fornecidos.
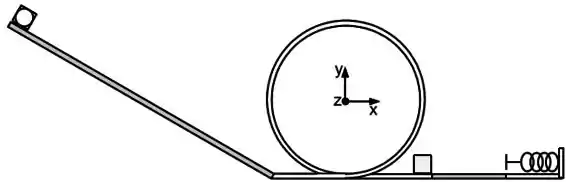
g) Após a colisão inelástica entre os dois blocos, o conjunto segue com velocidade pela superfície de comprimento que tem um coeficiente de atrito cinético que varia linearmente com a distância na forma quando utilizamos o valor de em metros. Calcule o trabalho realizado pelo atrito e a energia potencial elástica armazenada na mola quando ela estiver totalmente comprimida.
Ver solução completaQuestão 72
Considere o sistema da figura abaixo. O bloco de forma triangular possui massa e o que está sobre ele, . A rampa do bloco de baixo faz um ângulo com a horizontal. O coeficiente de atrito entre o bloco e a superfície é . Existe atrito entre os dois blocos, de coeficiente (estático igual ao cinético), mas este é pequeno e insuficiente para manter o bloco de massa parado sobre o de baixo, se o de baixo estiver parado. Uma força é aplicada sobre o bloco de baixo, como na figura, para acelerá-lo de tal forma que o bloco de cima não desliza sobre o de baixo, enquanto o conjunto se movimenta sobre o piso. Uma força é feita de forma que o conjunto se movimente sobre o piso, mas o bloco de cima continue sem se movimentar sobre o de baixo, com a força de atrito estático entre os blocos estando em seu limite máximo (o bloco de cima está na iminência de começar a SUBIR sobre o de baixo). Dê suas respostas em termos de e .
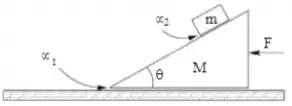
3) calcule a aceleração máxima do conjunto
Ver solução completaQuestão 73
Um cachorro de massa caminha preso a uma coleira inextensível e de massa desprezível. A outra extremidade da coleira está amarrada a uma mola de constante elástica , que pode distender-se sem atrito ao longo de um tubo horizontal. A outra extremidade da mola está fixa numa parede. O coeficiente de atrito entre o cachorro e o chão é e na situação mostrada na figura a mola está com a máxima distensão e o cachorro está na iminência de escorregar. Nesta situação:
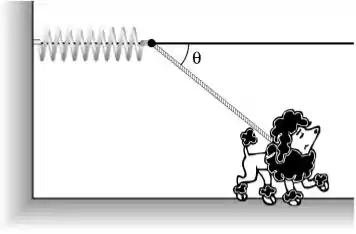
a) Monte o diagrama de forças agindo sobre o cachorro;
b) Qual é a máxima distensão da mola?
c) Qual a tração na corda?
NOTA: Nos itens (b) e (c), dê sua resposta em função das variáveis descritas no problema e de constantes, somente.
Ver solução completaQuestão 74
(Cap 6 – Ex 6) Um porco brincalhão escorrega em uma rampa com uma inclinação de e leva o dobro do tempo que levaria se não houvesse atrito. Qual é o coeficiente de atrito cinético entre o porco e a rampa?
Ver solução completa