Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 38
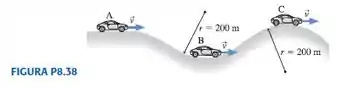
Três carros estão trafegando a na rodovia mostrada na FIGURA . O carro B encontra-se no fundo de um vale, entre as colinas, e o carro C, no topo de uma colina, tendo tanto o vale quanto a colina um raio de curvatura de . Suponha que, subitamente, cada carro seja freado fortemente e comece a derrapar. Quanto vale a aceleração tangencial (i.e., a aceleração paralela à rodovia) de cada carro? Considere que .
Passo 1
Olá, tudo bem?
Os passageiros desse brinquedo são grudados na parede se a força de atrito estático for suficiente para suportar a força peso deles, certo? Sendo assim a velocidade angular mínima vai ser aquela na qual a força de atrito estático é máxima.
Como o coeficiente de atrito das roupas possui uma faixa, vamos usar o menor valor, assim será mais seguro.
Então devemos igualar a força de atrito estático com o peso:
Mas a normal, nesse caso, deve ser igual a força centrípeta, então nossa equação fica assim ó:
E assim temos uma expressão para velocidade em função dos parâmetros do brinquedo e da massa da criança.
Passo 2
Mas o problema nos pede a velocidade angular! E não a tangencial! Bom, devemos lembrar que , então vou substituir na expressão ali de cima:
O diâmetro da trajetória vale , então o raio vale . O coeficiente de atrito estático é o inferior do intervalo e vale . A gravidade é , agora é só substituir tudo e jogar na calculadora:
O problema pede a velocidade em . Para transformar de para basta multiplicar a velocidade pelo fator .
Beleza?
Espero ter ajudado!
Vamos pra próxima?