Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 26.Exercícios - Ex. 40

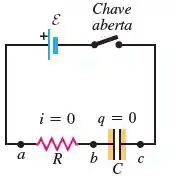
Você liga uma bateria, um resistor e um capacitor conforme indicado na Figura 26.20a, em que E 36,0 V, C 5,00 mF e R 120 V. A chave S está fechada em t 0. (a) Quando a voltagem através do capacitor é igual a 8,00 V, qual é o módulo da corrente no circuito? (b) Em que instante t após o fechamento da chave a voltagem através do capacitor é igual a 8,00 V? (c) Quando a voltagem através do capacitor é igual a 8,00 V, a que velocidade a energia está sendo armazenada no capacitor?

Passo 1

E aiii galera!

Tudo bom com vocês?

Vamos fazer mais uma questãozinha?

Quando S está fechado, a carga começa a fluir e carregar o capacitor até a diferença de potencial através do capacitor ser igual à fem da bateria.

Vamos usar:

V R = R I

V C = ε 1 - e - t R C

U C = Q 2 2 C

Passo 2

Letra a:

Aplicando a lei das malhas, temos:

V c + V R = ε

Então,

I = ε - V C R = 36.0 V - 8.00 V 120 Ω = 0.2333 A

Passo 3

Letra b:

De V C = ε 1 - e - t R C , temos e - t R C = 1 - V c ε

Resolvendo:

- t R C = ln ⁡ 1 - V c ε

t = - 120 Ω 5.00 μ F ln ⁡ 1 - 8.00 V 36.0 V = 151 μ s

Passo 4

Letra c:

U c = Q 2 2 C

Então,

P C = d U C d t = Q C d Q d t = V C I = 8.00 V 0.2333 A = 1.87 W

Resposta

  1. 0.2333 A
  2. 151 μ s
  3. 1.87 W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um capacitor de 4,60μ F inicialmente descarregado é conectado em série a um resistor de 7,50k Ω e a fonte de fem ε = 125V e que possuiresistencia interna desprezível. Imediatamnte após a conexão do ci
Uma capacitor de 1,50μ F está sentido carregado através de um resistor de 12,0Ω ligado a uma bateria de 10,0 V. Qual será a corrente quando o capacitor adquirir 1 4 da sua carga máxima? Será equivalen
No circuito indicado na Figura 26.58, ambos os capacitores têm carga inicial de 45,0 V. (a) Quanto tempo após a chave S ser fechada o potencial através de cada capacitor será reduzido a 10,0 V e (b) q
No circuito indicado na Figura 26.59, cada capacitor possui carga inicial de modulo igual a 3,50 nC em suas placas. Após a chave S ser fechada, qual será a corrente no circuito no instante em que os c
Quantas lâmpadas de 90 W e 120 V podem ser conectadas a uma fonte de 120 V com disjuntos de 20 A, sem fazer esse disjuntos saltar? (Veja a nota do Exercicio 26.18.)