Exercícios de Circuito RC - Lista de Exercícios Resolvida
Questão 1
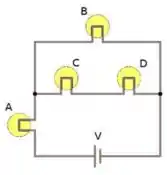
O interruptor está na posição da figura por um longo tempo. No instante ele é trocado para a posição . Determine a carga do capacitor e a corrente no resistor nos tempos:
No instante em que a chave é fechada.
Ver solução completa
Questão 2
O circuito da figura contém dois resistores e e dois capacitores e e o conjunto é ligado a uma bateria de . Antes de a chave ser ligada, os capacitores estão descarregados.
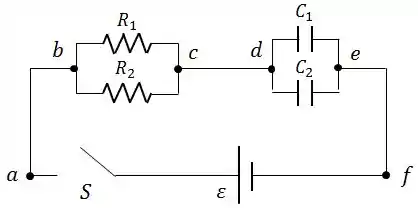
determine a constante de tempo desse circuito;
determine a corrente que atravessa a bateria em função do tempo após o fechamento da chave ;
determine a entre os ponto e em função do tempo;
com fechada por um longo tempo, quais são as cargas nos capacitores e .
Ver solução completaQuestão 3
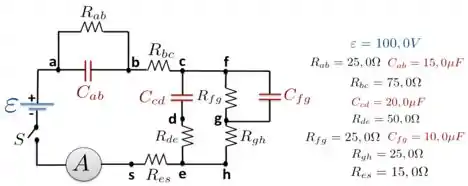
No circuito indicado na figura abaixo, os capacitores estão inicialmente descarregados, a bateria não possui resistência interna e o amperímetro é ideal. Ache a leitura do amperímetro:
- Logo após a chave S ser fechada;
- Após a chave estar fechada há muito tempo.
Questão 4
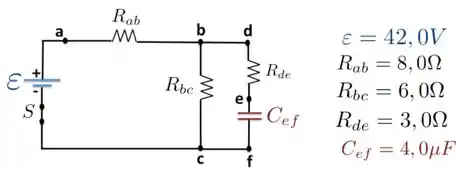
O circuito indicado na figura abaixo mostra um capacitor que está inicialmente descarregado. A chave está fechada no instante . Sobre essa situação,
- Qual é a corrente que passa através de cada resistor imediatamente após a chave ser fechada?
- Qual é a corrente que passa através de cada resistor imediatamente no instante de tempo ?
- Qual é a carga final do sobre o capacitor?
Questão 5
No circuito abaixo, , , .
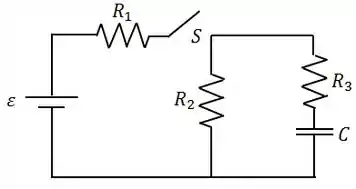
Com o capacitor completamente descarregado, a chave é fechada bruscamente no instante .
Determine, para o instante :
- A corrente no resistor 1;
- A corrente no resistor 2;
- A corrente no resistor 3;
- ;
- ;
- ;
- Em ;
- Em ;
- Faça um esboço do gráfico de em função do tempo no intervalo entre esses dois instantes extremos;
Determine, para (ou seja, após várias constantes de tempo):
Determine a diferença de potencial no resistor 2:
Questão 6
Um resistor de e um capacitor estão ligados em série, e então uma diferença de potencial de é repentinamente aplicada entre as extremidades deles.
A diferença de potencial entre as extremidades do capacitor aumenta para em .
- Calcule a constante de tempo do circuito;
- Determine a capacitância do capacitor;
Questão 7
O circuito abaixo apresenta capacitores de capacitância , inicialmente descarregados, e resistores de resistência . A força eletromotriz do circuito vale e a chave Ch está inicialmente aberta. Assinale a alternativa falsa.
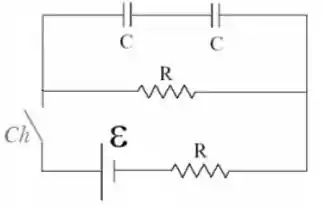
- No instante em que se fecha a chave, a intensidade da corrente que atravessa o resistor do ramo central é nula.
- Depois de muito tempo que a chave foi fechada, com os capacitores totalmente carregados, a ddp em cada resistor será igual a .
- Depois de muito tempo que a chave foi fechada, os capacitores estão totalmente carregados.
- Depois de muito tempo que a chave foi fechada, a intensidade da corrente nos resistores será igual a zero.
- Depois de muito tempo que a chave foi fechada, a corrente nos capacitores será igual a zero.
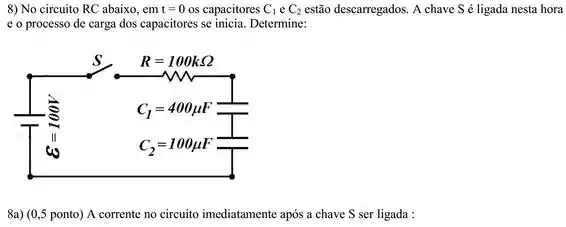
Questão 8
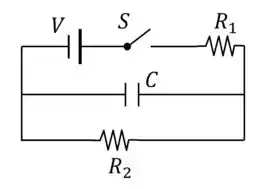
A vida útil de determinadas baterias termina quando elas fornecem toda a energia interna capaz de manter a sua . Considere uma bateria de e com capacidade de energia de . Suponha que a bateria seja ideal (sem resistência interna). Com esta bateria no circuito da Figura 1, onde , determine:
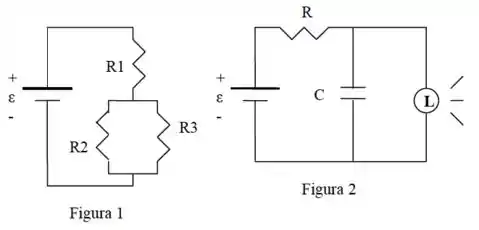
A potência fornecida pela bateria.
A vida útil neste circuito expressa em horas.
Uma nova bateria do mesmo tipo que a anterior é utilizada no circuito da Figura 2, onde e . Trata-se de um circuito de emissão repetitiva de “flashes” de luz. Quando a voltagem do capacitor atinge 2/3 do seu valor máximo, a lâmpada emite um “flash” de luz e descarrega-o instantaneamente, repetindo-se o ciclo.
O intervalo de tempo (período) entre “flashes”.
A quantidade de “flashes” emitidos durante a vida útil da bateria.
Em cada ciclo, a razão entre a energia armazenada em e a dissipada em .
Ver solução completaQuestão 9
No circuito da figura, os capacitores têm as seguintes propriedades:
- : inicialmente descarregados, ambos com meio de constante dielétrica e capacitância de .
- : Carga inicial de , tipo placas paralelas com vácuo entre elas e de capacitância igual a .
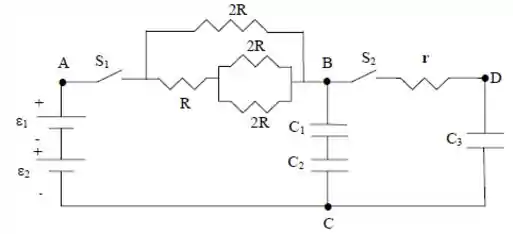
Nesse circuito, ocorrem as seguintes fases sucessivas:
- Fase 1: chave fechada e aberta durante longo tempo.
- Fase 2: Chaves abertas, o meio dielétrico de é substituído por vácuo e a separação das placas é alterada.
- Fase 3: chave aberta e fechada durante longo tempo.
Considerando , e , determine:
As d.d.p. em função do tempo durante a fase 1.
A carga em no final da fase 1.
Qual deve ser o aumento da separação das placas de durante a fase 2, para que a corrente no resistor seja nula durante toda a fase 3?
A diferença entre as energias armazenadas em na fase 1 e no final da fase 2.
Ver solução completaQuestão 10
No circuito abaixo têm-se:
, , , , , , inicialmente descarregados.
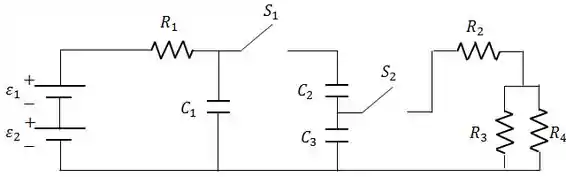
Considere que o circuito tem as seguintes fases sucessivas:
Fase 1: a chave é fechada e permanece aberta durante um tempo muito longo.
Fase 2: a chave é aberta, permanece aberta sendo o meio do capacitor substituído por outro de constante dielétrica duas vezes maior.
Fase 3: a chave permanece aberta e é fechada durante um tempo muito longo.
Determinar:
A carga armazenada em cada capacitor no final da fase 1.
A corrente que passa em em função do tempo durante a fase 1.
A energia fornecida por ambas as baterias durante a fase 1.
A corrente que passa em em função do tempo durante a fase 3.
A energia fornecida por na fase 3.
A potência máxima dissipada em durante a fase 3.
Ver solução completaQuestão 11
Considere o circuito RC da figura, onde , , é um capacitor de placas paralelas de área , com separação de , tendo um meio entre as placas de constante dielétrica , e . e são duas chaves.
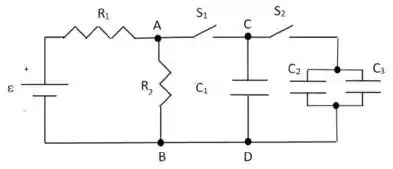
Todos os capacitores estão inicialmente descarregados. Neste circuito, ocorrem as seguintes fases sucessivas:
Fase 1: chave fechada e aberto durante longo tempo.
Fase 2: chaves e abertas e o dielétrico substituído por outro de .
Fase 3: chave aberta e fechada.
Fase 4: chaves e fechadas.
Determine:
- A capacitância .
- As correntes em e no instante inicial da fase 1.
- A energia armazenada em e a potência dissipada em no final da fase 1.
- O trabalho externo necessário para substituir o meio dielétrico na fase 2.
- A diferença de potencial no final das fases 1, 2 e 3.
- A corrente em (sentido e intensidade) no início da fase 4.
Em todos os cálculos, considere .
Ver solução completaQuestão 12
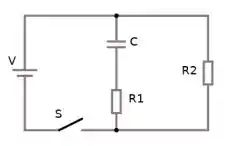
No circuito indicado na figura ao lado, o capacitor está inicialmente descarregado e o interruptor aberto. e são resistores. Em um instante inicial o interruptor é fechado.
c) Apresente a equação diferencial que rege a carga no capacitor em função do tempo, após o interruptor ser fechado.
Questão 13
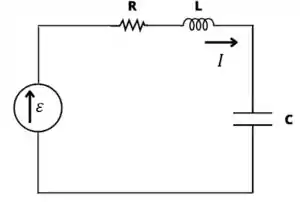
A figura abaixo mostra um circuito com uma fonte de voltagem alternada com força eletromotriz .Esta fonte de voltagem tem a frequência regulável. No regime estacionário se observou que a corrente fica em fase com a força eletromotriz quando a frequência da fonte tem o valor de . Não é fácil verificar se a corrente oscila exatamente em fase com a voltagem. Por esta razão a pessoa que fez a medida estimou uma incerteza deste valor de . O valor da capacitância vale e o valor da resistência vale . Determine o valor da indutância do circuito assim como a incerteza experimental deste valor.
Questão 14
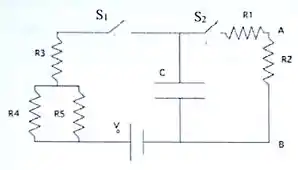
Um capacitor de placas planas e paralelas de área , com separação , tendo o vácuo como meio dielétrico, é conectado a um gerador de força eletromotriz através da chave e de três resistores iguais , dispostos como na figura. O circuito possui também outros dois resistores , conectados ao capacitor através da chave .
Em todos os cálculos considere: (base dos logaritmos neperianos), .
Considere as seguintes fases:
Fase 1: a chave está aberta e a chave é fechada por um tempo e depois aberta novamente.
Fase 2: com a chave aberta, a chave é fechada por muito tempo.
Determine:
(a) A capacitância do capacitor.
(b) A tensão e a carga do capacitor no final da Fase 1, ou seja, quando é aberta novamente. (Sugestão: analise a constante de tempo do circuito).
(c) A energia armazenada no capacitor durante o carregamento.
(d) A corrente que passa em e no instante de tempo após o início da Fase 2. (Sugestão: analise novamente a constante de tempo do circuito)
(e) A ddp (sobre ) no instante
(f) A energia total dissipada durante o descarregamento de até o instante
(g) A potência dissipada sobre e no instante
Ver solução completaQuestão 15
O interruptor está na posição da figura por um longo tempo. No instante ele é trocado para a posição . Determine a carga do capacitor e a corrente no resistor nos tempos:
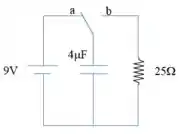
No instante em que a chave é fechada.
Ver solução completa
Questão 16
No circuito mostrado na figura abaixo, a chave é fechada no instante . A carga no capacitor nesse instante é . Considere , , , e .
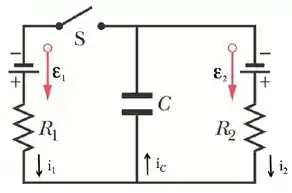
Para tal situação, calcule:
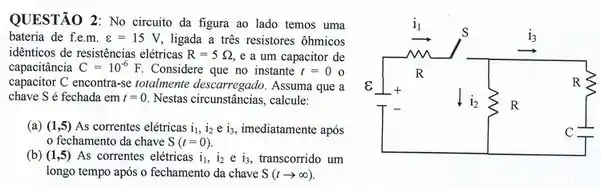
(a) As correntes , e no instante .
(b) As correntes , e para .
(c) A carga no capacitor quando o mesmo está totalmente carregado.
Ver solução completaQuestão 17
O circuito da Figura 1 abaixo é formado pelos elementos: , , , , e . Adicionalmente, apresenta as seguintes condições iniciais: chave aberta e capacitor descarregado.
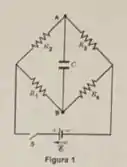
- Determine a corrente na bateria (indicando seu sentido) imediatamente após o fechamento da chave .
- Determine a diferença entre os potenciais , supondo que o capacitor está plenamente carregado.
- Após o pleno carregamento do capacitor, a chave é aberta. Determine a expressão para a diferença entre os potenciais em função do tempo, calculando seus valores numéricos. Indique o sentido da corrente no capacitor.
Questão 18
No circuito mostrado na figura, a chave está inicialmente averta e o capacitor está descarregado. A chave é então fechada no instante .
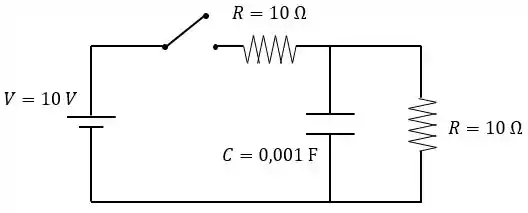
Qual é a diferença de potencial através do capacitor muito tempo após o fechamento?
Ver solução completa
Questão 19
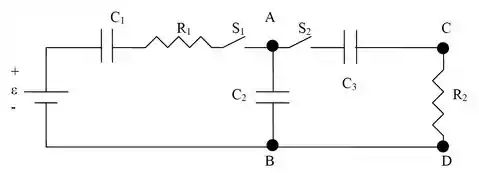
No circuito abaixo os capacitores e estão inicialmente descarregados e ocorrem as seguintes fases sucessivas:
Fase 1: chave fechada e aberta durante longo tempo;
Fase 2: chave abertas e o meio de substituído por outro de constante dielétrica vezes menor;
Fase 3: chave aberta e fechada durante longo tempo.
Considerando , determine com justificativa:
A corrente elétrica em função do tempo em durante a fase .
A energia dissipada em na fase .
A energia fornecida pela bateria na fase .
A d.d.p. no final da fase .
A energia armazenada em na fase .
A d.d.p. no início e final da fase .
As cargas em no final da fase .
Questão 21
Dois condutores e no vácuo são conectados diretamente a uma bateria cuja força eletromotriz é igual a , conforme mostra a figura. Uma das linhas de campo elétrico originadas pela configuração está alinhada com o eixo entre os pontos e da superfície dos condutores.
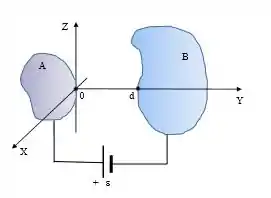
Ao longo desta linha, o campo é dado pela função:
onde é uma constante e é a carga (desconhecida) do condutor positivo. Determine:
(a) A carga com sinal dos condutores e , em função dos parâmetros da configuração (;
(b) A capacitância da configuração, em função dos mesmos parâmetros;
(c) A energia fornecida pela bateria, em função dos mesmos parâmetros;
(d) Se o vácuo é substituído por um meio de constante dielétrica igual a enquanto a conexão da bateria com os condutores é mantida, recalcule os itens (a), (b) e (c);
Em uma fase posterior, a bateria é removida e substituída por um resistor de resistência . Nesta condição, determine:
(e) A corrente no resistor em função do tempo;
(f) A ddp em função do tempo;
(g) A potência dissipada no resistor no início desta fase.
Ver solução completaQuestão 22
O capacitor no circuito da figura está inicialmente descarregado. Um longo tempo depois que a chave foi fechada, a diferença de potencial através de é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 23
Considere o circuito da Figura 1, onde e S é uma chave que alterna entre as posições 1 e 2 de forma cíclica, de tal forma que a permanência em cada posição tem a duração de 1 segundo.
- Desenhe o gráfico em escala da variação da . no capacitor com dois ciclos da chave S, indicando nos eixos os valores numéricos importantes. NOTA: considere .
- Determine para que a em no inicio da fase seja igual a .
- Com o valor de calcule a corrente fornecida pela bateria no inicio da fase .
-
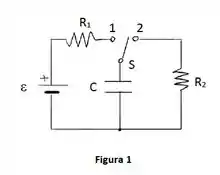
1 e o indutor na figura fossem plenamente energizados nos respectivos circuitos e depois conectados diretamente entre si, formando um circuito , qual seria a frequência angular de oscilação e a amplitude da voltagem do capacitor, após o sistema entrar em oscilação estável?
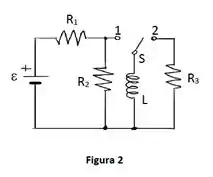
Considere agora o circuito da Figura 2, onde , o indutor está inicialmente sem energia e ocorrem as seguintes fases sucessivas:
- Fase 1: chave S na posição 1 durante longo tempo;
- Fase 2: chave S na posição 2 durante longo tempo.
Questão 24
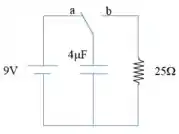
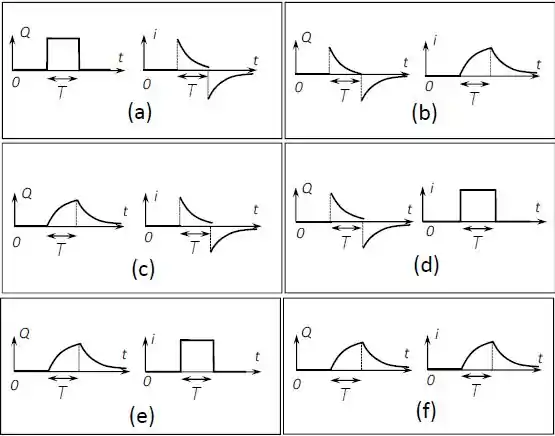
No circuito abaixo o capacitor está inicialmente descarregado. A chave é colocada na posição por um tempo e imediatamente depois é colocado na posição .
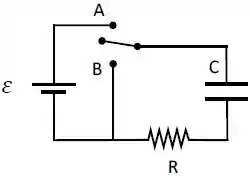
Indique os gráficos que melhor representam o comportamento da carga e da corrente, respectivamente, neste circuito.
Questão 25
Um resistor e um capacitor são conectados em série através de uma bateria ideal com uma voltagem constante entre seus terminais. Decorrido um tempo muito grande após a ligação do circuito podemos afirmar que a voltagem medida nos terminais do capacitor é:
(a) Igual à voltagem da bateria.
(b) Menor que a voltagem da bateria, porém maior que zero.
(c) Maior que a voltagem da bateria.
(d) Igual a voltagem do resistor.
(e) Nula
Ver solução completaQuestão 26
Para se carregar um capacitor num circuito em série, dobra-se o valor da fonte de tensão, então podemos afirmar que sua constante de tempo capacitiva:
(a) Dobra de valor.
(b) Fica reduzida a metade
(c) Fica quatro vezes maior
(d) Fica quatro vezes menor
(e) Permanece a mesma
Ver solução completaQuestão 27
Na figura temos um circuito formado por duas baterias, dois resistores, um capacitor e uma chave . Inicialmente a chave está aberta por um tempo muito longo.
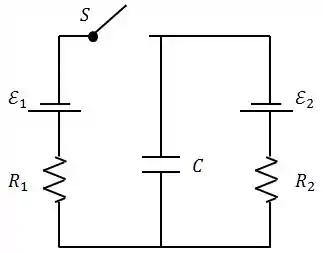
Nesta situação, determine a carga no capacitor ;
A chave é então fechada e mantida assim por muito tempo, determine:
As correntes nos resistores e ;
A diferença de potencial entre as placas do capacitor;
A variação da carga nas placas do capacitor.
Ver solução completaQuestão 28
Um capacitor está inicialmente descarregado. No instante , o capacitor é ligado em série a um resistor e a uma bateria. A energia do capacitor aumenta, atingindo um valor quando .
No instante igual à constante de tempo , a energia armazenada no capacitor é dada por:
;
;
;
;
;
Ver solução completaQuestão 29
Considere o circuito mostrado na figura.
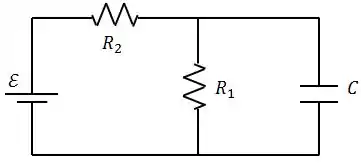
A fonte de fem tem resistência interna desprezível. Os resistores têm resistências e . O capacitor tem capacitância . Quando o capacitor está completamente carregado, o módulo da carga nas placas é .
O valor é:
;
;
;
;
;
Ver solução completaQuestão 30
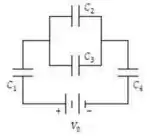
3ª questão - Na figura abaixo, os 4 capacitores estão completamente carregados. Determine a energia armazenada por , sabendo que , , , e .
A)
B)
C)
D)
E)
Ver solução completaQuestão 31
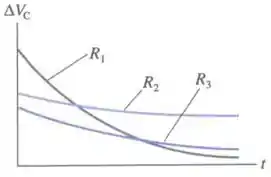
A figura abaixo mostra a voltagem em função do tempo de um capacitor enquanto ele é descarregado (separadamente) através de três diferentes resistores. Qual a alternativa que melhor descreve a relação entre a resistência destes três resistores?
(a)
(b)
(c) .
(d)
(e)
Ver solução completaQuestão 32
Considere o circuito da figura abaixo e determine:
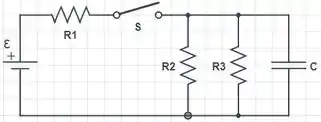
(a) a diferença de potencial através do capacitor após a chave ter estado fechada por um tempo muito longo;
(b) a energia armazenada no capacitor depois de um tempo muito longo.
Depois que a chave é aberta, calcule:
(c) a corrente em função do tempo que atravessa o capacitor;
(d) a energia que é dissipada no resistor durante o processo de descarga do capacitor.
Ver solução completaQuestão 33
No circuito abaixo, considere que inicialmente a chave esteve ligada na posição por um longo tempo. Repentinamente, a chave é trocada para a posição .
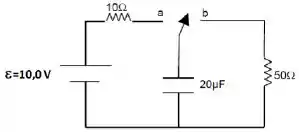
10a) A carga no capacitor quando a chave é trocada para a posição , é igual a:
10b) A carga no capacitor e a corrente no circuito depois da chave estar na posição é:
Ver solução completa
Questão 34
7ª questão - Um circuito RC em série é conectado a uma fonte ideal através de uma chave aberta. A chave é fechada no instante . Qual das seguintes afirmações sobre o circuito está correta?
A) O capacitor carrega até seu valor máximo em um intervalo de tempo igual a uma constante característica do circuito e a corrente é zero naquele momento
B) A diferença de potencial no resistor e a diferença de potencial no capacitor são sempre iguais
C) A diferença de potencial no resistor é sempre maior que a diferença de potencial no capacitor
D) A diferença de potencial no capacitor é sempre maior que a diferença de potencial no resistor
E) Uma vez que o capacitor está essencialmente totalmente carregado, não há corrente apreciável no circuito
Ver solução completaQuestão 35
No circuito da figura, a fonte tem e resistência interna , as resistências dos resistores são , e , e as capacitâncias dos capacitores são e .
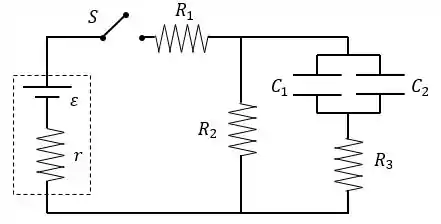
A chave permaneceu fechada por um tempo suficientemente longo para que os capacitores se carregassem totalmente. Nessa situação, calcule:
a corrente através da fonte;
a carga dos capacitores e ;
a diferença de potencial através de .
Com os capacites totalmente carregados, abre-se a chave .
Qual é a energia total dissipada no circuito?
Ver solução completaQuestão 36
O interruptor do circuito abaixo ficou por longo tempo na posição . Foi trocado para a posição em .
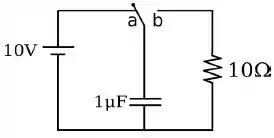
Qual é a carga no capacitor no tempo ?
Ver solução completa
Questão 37
Considere um circuito elétrico constituído por uma bateria ideal de fem , duas resistências e e um capacitor de capacitância , conforme a figura a seguir.
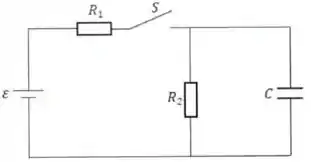
O circuito encontra-se inicialmente aberto (chave S aberta), com o capacitor totalmente descarregado. A chave S é então fechada e após um longo tempo, o capacitor acumula uma carga de . Quanto vale a fem da bateria?
Ver solução completa
Questão 38
Uma lâmpada incandescente é conectada a um circuito, como mostrado na figura abaixo, com uma chave aberta e com o capacitor totalmente descarregado. Considerando que a bateria tem uma resistência interna desprezível, quais dos gráficos melhor representa o brilho da lâmpada como um função do tempo , depois que a chave é fechada?
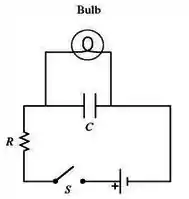
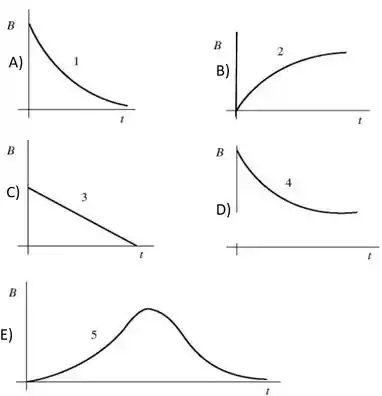
Questão 39
Um capacitor , inicialmente descarregado, é ligado em série a um resistor . A combinação é então ligada a uma bateria de . Espera-se um tempo suficiente até que uma corrente estacionária seja estabelecida.
Qual das seguintes afirmações NÃO é verdadeira?
a constante de tempo é independente de ;
a carga final em é independente de ;
a energia térmica gerada por é dependente de ;
a energia térmica gerada por é dependente de ;
a corrente inicial (imediatamente após a bateria ser ligada) é independente de ;
Ver solução completaQuestão 40
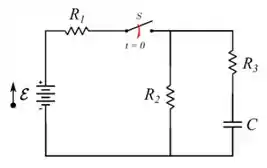
No circuito da figura abaixo a bateria é ideal e possui uma f.e.m. , o capacitor possui uma capacitância , e os resistores possuem resistências, e , todas em .
a) Com o capacitor totalmente descarregado, a chave é fechada bruscamente no instante. Determine para o instante , a corrente no resistor , a corrente no resistor e a corrente no resistor .
b) Após passado muito tempo, i.e., após ter passado várias constantes de tempo do circuito, determine a corrente no resistor , a corrente no resistor e a corrente no resistor .
c) Determine a diferença de potencial no resistor em e após muito tempo de fechada a chave, i.e., após ter passado várias constantes de tempo do circuito.
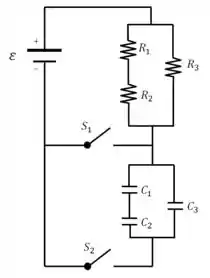
Questão 41
No circuito da figura, as chaves e estão inicialmente abertas e não há corrente no circuito. Dados: , , , , , . .
a) Calcule a resistência equivalente e a capacitância equivalente do circuito.
b) Se somente a chave é fechada, calcule a corrente em cada resistor. Desconsidere a resistência interna da fonte.
A partir daqui, considere apenas o circuito equivalente. Suponha que o capacitor equivalente está inicialmente descarregado e apenas a chave é fechada, criando um circuito .
c) Deduza a expressão da carga (medida em ) em função do tempo (medido em ).
d) Qual será a carga máxima armazenada no capacitor equivalente.
Questão 42
No circuito abaixo, no instante (chave aberta).
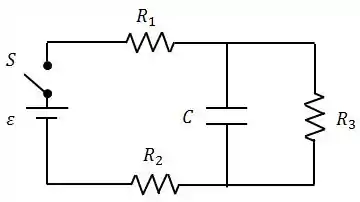
O capacitor encontra-se descarregado. Considerando que a bateria que alimenta o circuito é ideal e com força eletromotriz , calcule, após o fechamento da chave :
A corrente que atravessa o capacitor, imediatamente após o fechamento de ;
A corrente que passa pelo resistor , imediatamente após o fechamento de ;
A corrente que atravessa pela chave e a carga no capacitor em ;
A carga do capacitor e a corrente que atravessa os resistores e em função do tempo;
Ver solução completaQuestão 43
Na figura abaixo, a força eletromotriz da fonte ideal é , as resistências são e e o capacitor de capacitância está inicialmente descarregado. A chave é fechada em .
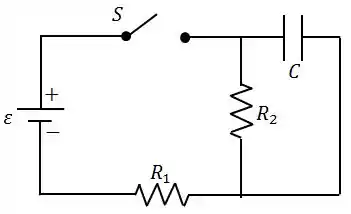
Determine, imediatamente após o fechamento de :
A corrente no resistor 1;
A corrente no resistor 2;
Transcorrido um tempo muito longo após o fechamento de , qual é a carga do capacitor?
Abrindo-se agora a chave , determine a corrente em em função do tempo;
Ver solução completaQuestão 44
Considere o circuito abaixo levando em consideração que a bateria é ideal, de força eletromotriz , e que o capacitor encontra-se descarregado inicialmente.
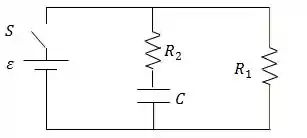
Após ligar a chave , no tempo , calcule:
- A corrente que passa pelo resistor ;
- A corrente que passa pela chave , imediatamente após ser ligada ;
- A carga do capacitor e a corrente que passa pelo resistor , em função do tempo;
Questão 45
O circuito da figura contém dois resistores e e dois capacitores e e o conjunto é ligado a uma bateria de . Antes de a chave ser ligada, os capacitores estão descarregados.
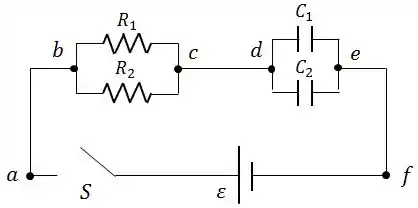
determine a constante de tempo desse circuito;
determine a corrente que atravessa a bateria em função do tempo após o fechamento da chave ;
determine a entre os ponto e em função do tempo;
com fechada por um longo tempo, quais são as cargas nos capacitores e .
Ver solução completaQuestão 46
Considere um circuito LRC em série onde . O capacitor é carregado com uma carga inicial e então o circuito é colocado para oscilar. Sabendo-se que o período da oscilação não amortecida é de e o coeficiente de amortecimento é , pede-se:
Escreva a equação da oscilação dom todas as constantes numéricas.
Calcule os valores da capacitância e da resistência.
Ver solução completaQuestão 47
Em um circuito oscilante com e , considere que a corrente inicial seja máxima. Calcule o tempo necessário para o capacitor carregar completamente pela primeira vez.
Ver solução completaQuestão 48
Um capacitor de capacitância está ligado em paralelo a um resistor de resistência , conforme a figura. No instante a carga do capacitor é e a chave é fechada.
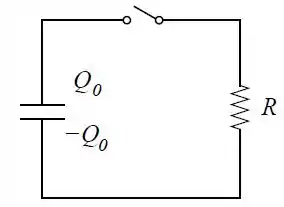
Escreva a equação diferencial para a carga na placa superior do capacitor para .
Calcule e para .
Calcule a energia armazenada no capacitor. Note que não é constante. Calcule e interprete o resultado.
Ver solução completaQuestão 49
(Cap 27 – Ex 66) A Fig. 27-67 mostra dois circuitos com um capacitor carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, e . Na Fig. 27-67b, e . A razão entre as cargas iniciais dos dois capacitares é . No instante , as duas chaves são fechadas. Em que instante os dois capacitores possuem a mesma carga?
Ver solução completaQuestão 50
(Cap 27 – 64) Um capacitor com uma diferença de potencial inicial de começa a ser descarregado através de um resistor quando uma chave é fechada no instante . No instante , a diferença de potencial no capacitor é .
a) Qual é a constante de tempo do circuito?
b) Qual é a diferença de potencial no capacitor no instante ?
Ver solução completaQuestão 51

ATENÇÃO: Ignorem o texto em inglês que se encontra nesse site, abaixo da figura. O que importa são as instruções fornecidas aqui. Utilizando os 2 últimos dígitos do RA do Aluno 1 (considerem que estes formam um único número de 2 dígitos; p. ex., se o RA é 123456, o número a ser usado será 56), calculem o valor da resistência a ser usado:
Tirem um print da tela mostrando a seleção da resistência na simulação e mostrem abaixo (podem selecionar o valor de 𝑅 na simulação o mais próximo possível do valor calculado):
a) Utilizando o gráfico da simulação calculem o valor da capacitância , descrevendo qual o procedimento utilizado. Tirem prints dos pontos selecionados do gráfico e colem estes na resolução de vocês.
Com a chave obrigatoriamente na posição open:
b) Deduzam a expressão da energia dissipada no resistor em função do tempo, partindo da equação da potência, .
c) Calculem a energia dissipada no resistor após um tempo , onde é a constante de tempo característica do circuito. Qual o valor da constante ? Qual o significado da constante ? Para o parâmetro , usem os últimos dígitos de seus RAs:
Ver solução completaQuestão 52
No circuito da figura abaixo, o capacitor está inicialmente descarregado e com a chave aberta. Neste circuito, a fem vale , as resistências valem e a capacitância do capacitor vale . Em a chave é fechada e permanece nessa posição por um tempo muito maior que a constante de tempo capacitiva. Depois de decorrido esse tempo, a corrente que circula na resistência
é:
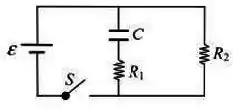
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 53
Qual é a constante de tempo do circuito mostrado na figura?
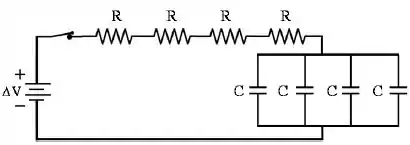
Cada um dos quatro resistores tem resistência , e cada um dos quatro capacitores tem capacitância . A resistência interna da bateria é desprezível.
Nenhuma das alternativas
Ver solução completaQuestão 54
Considere o circuito mostrado na figura. Na figura, a força eletromotriz , as resistências e e a capacitância . No início a chave está aberta e o capacitor está descarregado. No instante fechamos a chave.
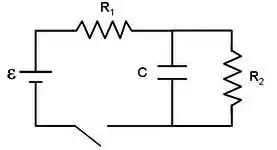
(a) Calcule a corrente passando nos resistores e no instante .
(b) Calcule a corrente passando nos resistores e após um tempo longo o suficiente para o sistema atingir o regime estacionário.
(c) Calcule a potência dissipada no resistor nesse regime estacionário.
Ver solução completaQuestão 55
(a)
(b) Zero
(c)
(d)
(e)
Após a chave ser ligada...
![]()
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 56
No circuito da figura abaixo, o capacitor está inicialmente descarregado.
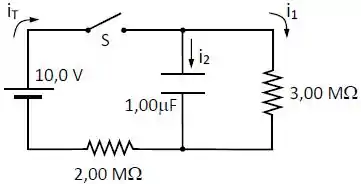
Em a chave é fechada.
Determine as correntes , e em .
Determine as correntes , e para .
Determine a carga no capacitor para .
Suponha agora que a corrente e a carga sejam dadas por
Use os resultados anteriores para determinar as constantes .
Ver solução completaQuestão 57
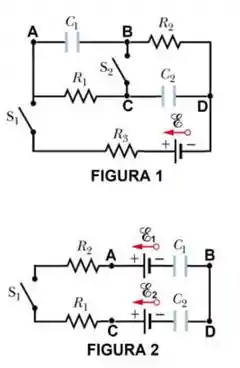
Considere o circuito da Figura 1, onde os valores de , são constantes e conhecidos. Inicialmente, os capacitores e estão descarregados e as chaves e abertas. Os capacitores e são carregados fechando-se as duas chaves simultaneamente. Em função dos dados do problema:
a) Apresente expressões para as tensões V1 e V2 e para as energias e armazenadas nos respectivos capacitores, supondo que ambas as chaves permaneceram fechadas durante muito tempo. Considere agora o circuito da Figura 2, onde os valores de , e são constantes e conhecidos. Inicialmente, os capacitores e estão descarregados e a chave S1 aberta. No instante , a chave é fechada e assim permanece por muito tempo. Em função dos dados deste novo problema:
b) Apresente expressões para as cargas nos capacitores e em função do tempo.
c) Apresente uma expressão para a tensão no resistor R1 em função do tempo.
d) Apresente expressões para as tensões e em função do tempo.
Questão 58
Um resistor e um capacitor, inicialmente descarregado, estão conectados em série com uma bateria ideal com voltagem constante através de seus terminais.
2) No instante em que a fonte é ligada, a voltagem através do capacitor é:
(a) igual ao dos terminais da bateria.
(b) menor que o dos terminais da bateria, mas maior que zero.
(c) igual à diferença de potencial sobre o resistor.
(d) zero.
(e) não há como saber, já que é um processo dinâmico.
3) No mesmo instante, a voltagem sobre o resistor é:
(a) igual ao dos terminais da bateria.
(b) menor que o dos terminais da bateria, mas maior que zero.
(c) igual à diferença de potencial sobre o capacitor.
(d) zero.
(e) não há como saber, já que é um processo dinâmico.
Ver solução completaQuestão 59
Um circuito é conectado a uma fonte de tensão por meio de uma chave que inicialmente está aberta. A chave é fechada em .
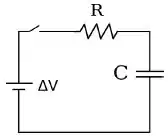
Considerando este circuito, qual das seguintes sentenças está CORRETA?
O capacitor fica completamente carregado no tempo 𝝉 e a corrente é nula neste instante.
A diferença de potencial através do resistor é sempre igual a do capacitor.
A diferença de potencial através do resistor é sempre maior que a do capacitor.
A diferença de potencial através do capacitor é sempre maior que a do resistor.
Quando o capacitor estiver completamente carregado, não haverá corrente elétrica no circuito.
Ver solução completaQuestão 60
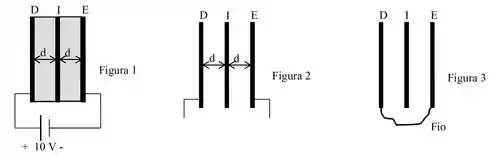
Duas placas paralelas condutoras de área , separadas de uma distância pelo meio dielétrico de permissividade elétrica , constituem um capacitor cuja capacitância aproximada é dada por:
Baseado nisso, considere a configuração da Figura , constituída de uma bateria e três placas paralelas condutoras de determinada espessura não desprezível e equivalente a uma combinação de dois capacitores. As placas estão inicialmente descarregadas, têm áreas iguais a cada uma e estão separadas de por meios dielétricos iguais de constante dielétrica . (Nos cálculos, utilize: )
Considere as seguintes fases sucessivas:
Fase :
As placas e são conectadas a uma bateria de fem igual a , conforme a Figura . Nesta situação, determine:
As cargas elétricas, com sinais, das placas , e .
A energia total armazenada nas regiões entre as placas.
Fase :
A bateria é removida e, a seguir, os meios dielétricos entre as placas são substituídos pelo vácuo, conforme mostra a Figura . Nesta situação determine:
As d.d.p entre as placas: , e .
O trabalho externo necessário para remover os dielétricos.
Fase :
As placas e são conectadas entre si durante longo tempo por um fio com resistência de , conforme mostra a Figura . Nesta fase, determine:
A intensidade e o sentido da corrente elétrica no fio em função do tempo.
A energia dissipada no fio
A carga elétrica das placas ao final desta fase.
Questão 61
(Cap 27 – 57) A chave S da Fig. 27-63 é fechada no instante ,fazendo com que um capacitor inicialmente descarregado de capacitância comece a se carregar através de um resistor de resiscência . Em que instante a diferença de potencial entre os terminais do capacitor é igual à diferença de potencial entre os terminais do resistor?
Ver solução completaQuestão 62
(Cap 27 – 60) Um capacitor com uma carga inicial é descarregado carregado através de um resistor. Que múltiplo da constante de tempo é o tempo necessário para que o capacitor descarregue
a) um terço da carga inicial;
b) dois terços da carga inicial?
Ver solução completaQuestão 63
4 - Um capacitor é carregado até armazenar uma energia de . Ao ser descarregado através de uma resistência , qual a máxima corrente que circula no circuito?
Questão 64
Dispõe-se de um capacitor de placas planas e paralelas com capacitância de . Deseja-se que haja uma corrente de deslocamento entre as placas do capacitor igual a . Qual a variação da diferença de potencial que deve existir nas extremidades deste capacitor?
Dados:
Ver solução completaQuestão 65
No circuito mostrado na figura, as resistências têm o mesmo valor de , a bateria é assumida como sendo ideal e o interruptor está inicialmente aberto. Ao se fechar a chave (interruptor), o capacitor inicia sua carga com um tempo característico . Após um longo intervalo de tempo a chave é novamente aberta e inicia-se a descarga do capacitor com um tempo característico . Quanto vale a razão ?
(a)
(b)
(c)
(d)
(e)
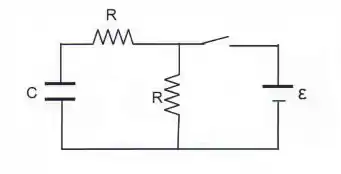
Questão 66
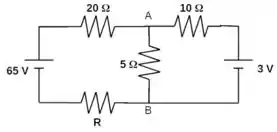
4ª questão - No circuito a seguir, um voltímetro verificou que há uma queda de potencial elétrico entre os pontos e (com ) igual a . Determine o valor da resistência .
A)
B)
C)
D)
E)
Ver solução completaQuestão 67
No circuito da figura, o capacitor está inicialmente descarregado.
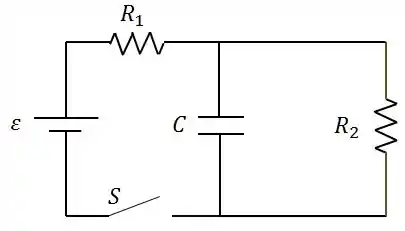
- Imediatamente após a chave ser fechada, qual é a corrente no resistor ?
- Qual é a potência dissipada no resistor ?
- Transcorrido um tempo muito longo após o fechamento da chave , qual é a energia acumulada no capacitor?
- Abrindo-se a chave , qual é a corrente no resistor em função do tempo?
- Qual é a energia total dissipada no processo de descarga do capacitor?
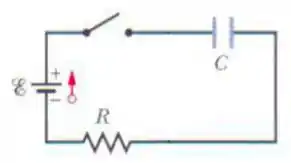
Questão 68
Na figura abaixo temos um circuito formado por um resistor, um capacitor e uma bateria ideal. Inicialmente, o capacitor se encontra descarregado. Se a chave for ligada, quanto tempo, em unidade de , levará para o capacitor atingir da sua carga máxima?
Questão 69
Considere o circuito ao lado, onde os valores de , , , e são conhecidos e os capacitores , e encontram-se inicialmente descarregados. Em seguida, os capacitores e são carregados fechando-se a chave e mantendo-se a chave aberta.
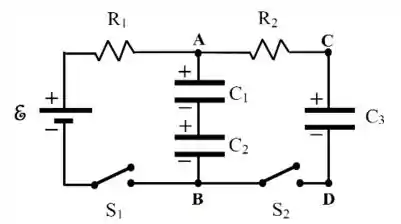
a) Apresente uma expressão para tensão (ddp) no resistor em função do tempo, a partir do instante em que a chave é fechada.
b) Calcule também a energia total armazenada nos dois capacitores e , supondo que a chave permaneceu fechada durante muito tempo.
Agora considere que seja aberta, depois de ter permanecido fechada durante muito tempo. Sabe-se que, neste instante, . Simultaneamente, os capacitores e são conectados ao capacitor descarregado fechando-se a chave que assim permanece durante muito tempo.
c) Calcule as tensões (ddps) finais entre os terminais dos capacitores e .
d) Calcule a energia total armazenada nos capacitores e ao final do processo. Compare com a energia armazenada nos capacitores e imediatamente antes do fechamento da chave . Por que elas são diferentes?
Ver solução completaQuestão 70
Todos os elementos do circuito da Figura ao lado são conhecidos. Inicialmente, os capacitores e estão descarregados e a chave aberta.
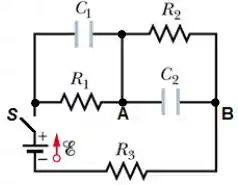
a) Determine a corrente na bateria (indicando seu sentido) imediatamente após o fechamento da chave .
b) Determine a corrente na bateria (indicando seu sentido) muito tempo após o fechamento da chave .
c) Determine as tensões nos capacitores e (indicando seus sentidos) muito tempo após o fechamento da chave , assim como as energias neles armazenadas.
d) Após os plenos carregamentos dos capacitores, a chave e a bateria são substituídas por um curto e o capacitor é retirado do circuito e no seu lugar nada é colocado. Determine a resistência equivalente observada a partir dos terminais A e B. Em seguida, caracterize totalmente a corrente no capacitor em função do tempo (indicando seu sentido).
Ver solução completaQuestão 71
No circuito mostrado na figura abaixo, a chave é fechada no instante . A carga no capacitor neste instante é .
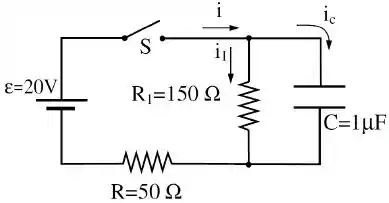
Para tal situação, calcule:
As correntes e no instante .
As correntes e para .
A energia potencial elétrica acumulada no capacitor, quando o mesmo está totalmente carregado.
A constante de tempo do circuito.
Ver solução completaQuestão 72
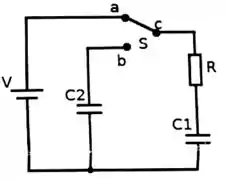
2 – No circuito da figura ao lado, uma fonte de está inicialmente ligada a uma chave , que pode ser configurada para ligaros pontos ou . Em cada ramo do circuito há um capacitor, ou , e um resistor em série com o capacitor . Os capacitores encontram-se descarregados inicialmente.
a) Quando a chave está na posição (a mesma da figura), temos a carga do capacitor . Supondo que a carga inicial deste capacitor seja nula, encontre a tensão no capacitor no instante inicial e após um longo tempo, quando o capacitor estiver totalmente carregado.
Questão 73
2 – No circuito da figura ao lado, uma fonte de está inicialmente ligada a uma chave , que pode ser configurada para ligaros pontos ou . Em cada ramo do circuito há um capacitor, ou , e um resistor em série com o capacitor . Os capacitores encontram-se descarregados inicialmente.
b) Depois de um longo tempo, a corrente cessa no resistor . Neste instante, a chave é colocada na posição , e a contagem do tempo é zerada. Apresente a equação diferencial que rege as cargas dos capacitores e a corrente com o tempo.
c) Lembrando que a carga inicial do capacitor é nula, encontre uma expressão que descreve a corrente em função do tempo da nova configuração do circuito, com a chave na posição .
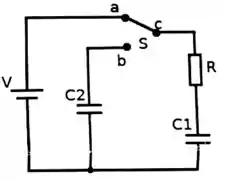
Questão 74
No circuito abaixo, a bateria de é ideal e o capacitor encontra-se inicialmente descarregado.
Após ligar a chave , em , calcule:
A corrente que passa pelo resistor ;
A corrente que passa pela chave , imediatamente após ser ligada ;
A carga do capacitor em função do tempo;
A corrente através de em função do tempo;
Ver solução completaQuestão 75
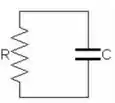
14 - Um capacitor de capacitância e, inicialmente, totalmente carregado com carga , é descarregado através de um resistor de resistência através de fios ideais (Veja a figura ao lado). O campo magnético muito próximo do fio inferior (ou seja, a uma distância muito pequena do fio quando comparada ao seu comprimento) decairá a metade após:
Questão 76
5 - Um capacitor de capacitância é descarregado ao formar um circuito com um resistor de resistência de . Quanto tempo leva para o capacitor perder metade de sua energia armazenada inicialmente?
Questão 77
5 - Um capacitor de é conectado a uma fonte cuja fem aumenta uniformemente com o tempo a uma taxa de . A corrente de deslocamento entre as placas é:
- .
Questão 78
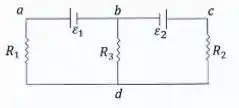
No circuito da figura abaixo:
- Determine as correntes em cada ramo.
- Calcule a diferença de potencial entre os pontos e .
- Calcule a potência fornecida por cada bateria.
Considere , , , e .
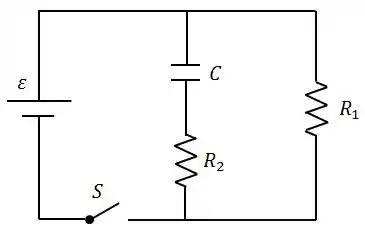
Questão 79
No circuito indicado na figura ao lado, o capacitor está inicialmente descarregado e o interruptor aberto. e são resistores. Em um instante inicial o interruptor é fechado.
d) Obtenha uma expressão que dê a corrente na fonte em qualquer instante de tempo após o interruptor ser fechado.
Questão 80
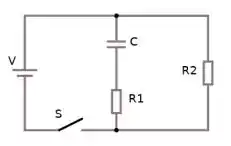
No circuito da figura, a chave S é fechada em . Qual é a carga no capacitor quando ?
- ;
- ;
- ;
- ;
- .
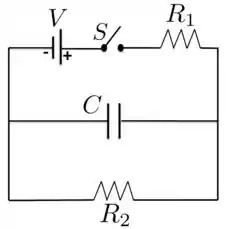
Questão 81
Considere o circuito da figura onde , , , , , e . Os capacitores são de placas planas e paralelas separadas de e têm capacitâncias dadas por . Todos os capacitores estão inicialmente descarregados. Neste circuito, ocorrem as seguintes fases sucessivas:
Fase 1: chaves e fechadas simultaneamente e aberta durante um longo tempo.
Fase 2: chaves , e abertas e, a seguir, a separação das placas de é triplicada e a de é duplicada.
Fase 3: chaves e abertas e fechada durante um longo tempo
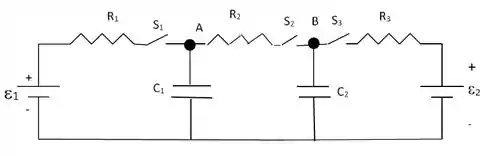
Determine:
- A diferença de potencial em função do tempo durante a Fase 1
- A energia armazenada nos capacitores no final da fase 2
- A intensidade e sentido da corrente em no início da fase 3
- O trabalho necessário para aumentar a separação das placas do capacitor e a força externa mínima (sem aceleração) na Fase 2. (Sugestão: lembre-se que , sendo a distância entre as placas)