Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 10.Problemas - Ex. 72
Você está projetando um sistema para movimentar cilindros de alumínio do solo para uma doca de carga. Você usa uma rampa de madeira resistente, com 6,00 m de extensão e inclinada em 37,0º acima da horizontal. Cada cilindro é preso por uma alça leve e sem atrito, passando pelo seu centro, e uma corda leve (porém forte) é presa a essa alça. Cada cilindro é uniforme e possui massa de 460 kg e raio de 0,300 m. Os cilindros são empurrados rampa acima, aplicando-se uma força constante à ponta livre da corda. é paralela à superfície da rampa e não exerce torque sobre o cilindro. O coeficiente de atrito estático entre a superfície da rampa e o cilindro é 0,120. (a) Qual é o maior módulo que pode ter, de modo que o cilindro ainda role sem deslizar enquanto sobre pela rampa? (b) Se o cilindro partir do repouso na base da rampa e rolar sem deslizar enquanto sobe, qual é o menor tempo que ele levará para alcançar o topo da rampa?
Passo 1
E aiiiiiiiii galera, tudo bom com vocês?
Vamos fazer mais uma questão!!
Letra a:
A seguir, temos o diagrama de corpo livre para ilustrar:
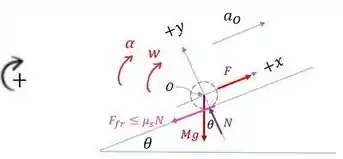
é no sentido horário, pois o cilindro está rolando para cima. é no sentido horário, pois está aumentando enquanto o cilindro está rolando para cima.
Observe que é para baixo porque esta é a força que produz o torque líquido necessário para o movimento de rolamento. Deve ser coerente com a direção de .
Rolar sem escorregar significa .
Passo 2
Temos as seguinte equações para moldar o problema:
Como o cilindro rola sem escorregar:
A força máxima para o cilindro rolar para cima sem escorregar.
Passo 3
Letra b:
Usando a F máxima, então a aceleração constante máxima do centro de massa é .
Com esta aceleração, o tempo de baixo para cima será o mais curto para o cilindro rolar sem escorregar.
Então,