Posição e Fase do MHS
Produzido por Leonardo de BemTeoria
Até agora nós vimos equações que descrevem o MHS, que são equações desse tipo:
Equação da posição:
Lembrando que na equação da posição poderia aparecer um seno também, mas na maioria das vezes aparece como cosseno mesmo.
Bora fazer um exemplo aqui, uma máquina de medir a força do golpe tem uma mola acoplada a plataforma como mostrada na figura
E tem a seguinte equação da posição.
Para essa equação, esboçar o gráfico do movimento.
Vamos trazer rapidinho quem é cada um nessa parada!
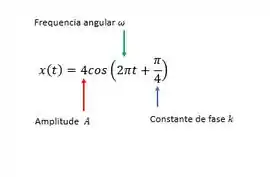
Para montar o gráfico, nossa maior preocupação é encontrar os pontos de máximo/mínimo onde a derivada da função vale 0 e onde a função corta a origem que é
Como a função é cosseno a gente sabe que o resultado do cosseno fica sempre nos limites [-1,1], então o gráfico vai variar no intervalo [-A, A]. Sabendo que esses são os valores máximos e mínimos a gente não precisa usar derivada vamos analisar a equação:
Ponto mínimo:
Como a gente falou o mínimo do gráfico que é um cosseno é a amplitude multiplicada pelo menor valor de cosseno que é sempre -1.
Assim:
Aqui temos que:
A gente sabe que , então:
Cortando , temos:
E isolando t, para a função de valor -4.
Ponto máximo:
Seguiremos a mesma ideia e aqui já podemos dizer que o máximo é quando o cosseno da função é 1.
A gente sabe que , também poderíamos usar cos(0) porém nos daria um tempo negativo, o que não é muito legal de trabalhar.
E enfim isolando e lembrando que é para quando a função vale 4.
Ponto onde
E por último a função pra ser zero precisa ter algum múltiplo de que não seja múltiplo de e como escolhemos o intervalo é interessante pegarmos alguém entre os dois vamos escolher .
Daí o argumento do cosseno deve ser
Enfim isolando totalmente t e lembrando que é t para quando a função dá zero:
Esses são os pontos mais importantes pra você esboçar o seu gráfico, a partir disso o movimento será repetido vamos esboçar o trecho inicial, também é interessante saber quanto vale só pra saber da onde a gente vai partir.
Desenhando então o gráfico:
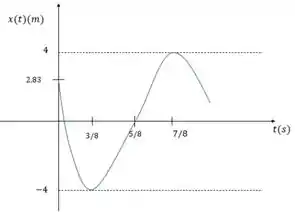
Agora já sabemos montar o gráfico!! Mas e interpretar ele? Bom, vamos ver as características mais importantes dele, então, pra gente sair daqui craque, sabendo tudo!
Características gerais
Os gráficos seguirão o padrão seno ou cosseno, como nos exemplos abaixo:
Gráfico de função cosseno:
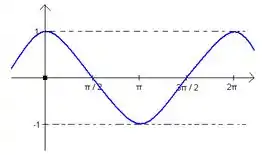
Características.
O gráfico deu uma função cosseno tem valor 1, quando o argumento da função é zero então na origem começa no valor máximo, e valor -1 quando o argumento é . Cuidado só que no MHS traçamos os gráficos posição x tempo, então acabam sendo gráficos um pouco diferentes já que o argumento da função depende de outros fatores.
Gráfico de função seno:
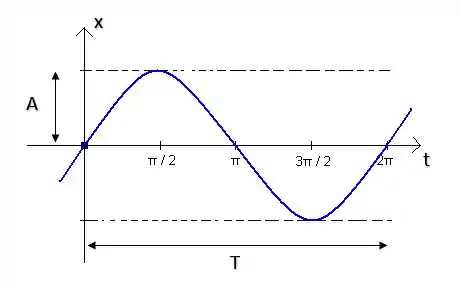
Características.
O gráfico deu uma função seno tem valor 1, quando o argumento da função é , e valor 0 quando o argumento é ou .
No segundo gráfico, temos uma marcação: Essa é a nossa amplitude - maior distância atingida em .
Período
O período vai ser o intervalo de tempo que o MHS leva pra repetir um ciclo.
Esse ciclo geralmente terá uma dessas duas aparências:
Assim:
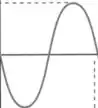
Ou assim:
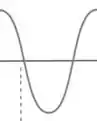
Beleza, para achar o período é só pegar o intervalo de tempo entre os extremos.
Observação: Caso o gráfico esteja deslocado (com uma fase), tente visualizar esses espaços no gráfico deslocado também. O importante é lembrar que o período sempre gera um ciclo completo.
A partir do valor do período, você pode calcular a frequência angular:
E a frequência do movimento que é dada por:
Fase
E se o gráfico não começar no 0 ou na amplitude? E se começar assim:
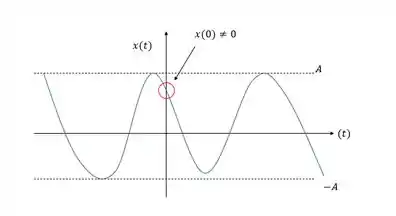
Nesse caso, teremos uma constante de fase diferente de 0 e como encontrar?
Então, se a função for do tipo:
E o valor em for , teremos que fazer:
E assim descobriremos o valor da nossa constante de fase.
Movimento Circular no MHS
Você sabia que um MHS pode ser interpretado como a projeção de um MCU (movimento circular uniforme)? Então, vamos ver isso com calma! Dá uma olhada no sistema massa-mola abaixo:
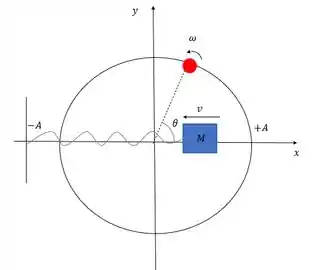
Onde o ângulo de fase é dado por:
é a amplitude do movimento, que é o raio do círculo.
é a velocidade angular do MCU e também a frequência angular do MHS
E agora, diga se esse ângulo de fase é positivo ou negativo.
Repare que o bloco é a projeção do ponto vermelho que percorre o círculo mas qual o motivo dessa associação? Fazer isso nos ajuda a definir o sinal do ângulo de fase.
O ângulo de fase é positivo quando a gente tem a partícula indo de para ou de 0 a ou seja:
e é negativo quando a partícula vai de para ou de a .
E no nosso caso o bloco tá indo para esquerda, ou seja de para então o nosso ângulo é positivo.
Características gerais
Período
Fase
Movimento Circular no MHS
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-P2-2015.1-2
Os gráficos abaixo descrevem o movimento de quatro osciladores harmônicos simples. Assinale a alternativa INCORRETA:
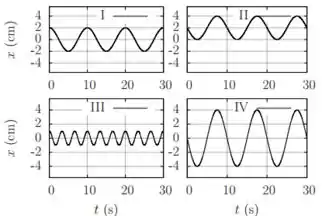
- Todos, exceto oscilam com período de
- e partem de sua posição de equilíbrio em
- e oscilam com a mesma amplitude.
- oscila com frequência menor que todos os restantes.
- realiza oscilações por minuto.
Passo 1
Bom, galera, o macete aqui é tentar comparar o período e a frequência de cada MHS.
Lembrando que: período é o tempo necessário para que um ciclo seja realizado e frequência é o número de oscilações por segundo.
Passo 2
Então, de cara, qual é o movimento que tem mais oscilações por segundo, ou seja, maior frequência?
É só a gente comparar quantas “ondinhas” cada MHS tem, num mesmo espaço de tempo.
Sacou?
Bom, se você entendeu certinho, percebeu que é o que tem a maior frequência. (:
Passo 3
Logo, como a d) nega isso, ela é a INCORRETA!
Resposta
d)
Exercício Resolvido #2
UFRJ-P2-2013.1-M07
A figura abaixo mostra um gráfico de posição tempo de um oscilador harmônico simples:
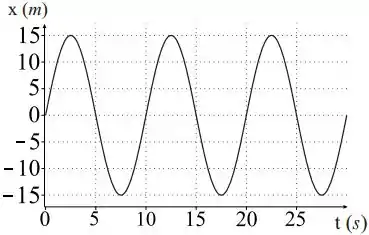
A função que melhor descreve o movimento do oscilador harmônico mostrado no gráfico acima é dada por:
Passo 1
A função nesse caso é
Onde
Passo 2
Pelo gráfico, o período vai ser:
Então:
Além disso, pode-se ver que:
Passo 3
Vamos agora achar o valor da fase.
Basta pegar um valor qualquer da função e resolver a equação. Em :
Então:
Ou:
Precisamos saber qual dos dois casos é o válido.
Passo 4
Vamos pegar outro ponto:
Veja que no ponto . Isso que eu to usando aqui!
Vamos ter:
Como os ângulos que tem cosseno igual a um são e zero, vamos ter:
Podíamos ter também:
Que é o mesmo ângulo, só que um é escrito de forma negativa e outro de forma positiva, mas são equivalentes. Vamos usar a negativa, porque as alternativas não tem . Logo:
Resposta
Letra D
Exercício Resolvido #3
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 106-10
Qual é a constante de fase do oscilador harmônico cuja função posição aparece na figura abaixo, se a função posição é da forma ? A escala do eixo vertical é definida por = 6,0 cm.
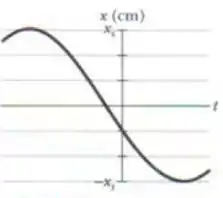
Passo 1
Bom, se , cada divisão do gráfico em representa , já que temos 3 divisões da origem até .
Beleza. E para , qual será o valor da função?
Como a curva encontra o eixo na primeira divisão abaixo da origem, temos:
Além disso, olhando no gráfico de novo, vemos que a maior “altura” é
Logo, essa é a amplitude do MHS:
Passo 2
Pra descobrir a fase, então, basta que a gente aplique o valor da função em
Assim, a fase vai ser o arco cujo cosseno é
Mas também podemos ter . E agora, como saber qual o certo?
Passo 3
Podemos ver o seguinte: a derivada da curva num ponto é igual a inclinação da reta tangente naquele ponto, certo?
Então, pegando o ponto , teremos:
Temos que . Como podemos ver na figura, a inclinação da reta tangente é negativa em . Logo, devemos ter:
Assim, concluímos que .
Resposta
Exercício Resolvido #4
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 110-66
A figura abaixo mostra a posição de um bloco oscilando em MHS na extremidade de uma mola . Quais são
a) a velocidade e b) o módulo da aceleração radial de uma partícula circular uniforme correspondente?
Passo 1
a)
Bom, a gente quer achar a velocidade do MCU correspondente a esse MHS.
Lembre-se que a velocidade do MCU pode ser escrita como:
Onde, no caso, , ou seja, o raio do MCU é igual a amplitude do MHS.
Olhando no gráfico, percebemos que
Então:
Mas não sabemos o valor de . Porém, fica fácil descobrir pelo gráfico o valor do período. Olhando direito, percebemos que ;
Assim:
Assim:
Passo 2
b)
A aceleração radial da qual o enunciado fala é a aceleração centrípeta.
Essa é dada por:
Agora é só fazer e substituir os valores:
Resposta
a)
b)
Exercício Resolvido #5
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 112-100-Modificada
Qual é a constante da fase do oscilador harmônico cuja função aceleração aparece na Fig. 15-56 se a função posição é da forma e ?
Passo 1
Aqui a gente vai seguir o nosso esquema pra determinar a fase do oscilador. Porém, temos uma diferença: o nosso gráfico é da aceleração, já a função dada, do deslocamento.
Assim, precisamos lembrar que se:
Perceba que a gente apenas derivou ali em cima.
Passo 2
Agora vamos olhar no gráfico: o é a quarta divisão na escala vertical. Logo, como , cada divisão valerá
Pelo gráfico, a gente consegue perceber que o valor da aceleração quando vale .
Passo 3
Assim, podemos dizer que:
Repare que aqui o é a amplitude da aceleração, que vale:
Como o gráfico que temos é da aceleração, podemos usar o direto como a amplitude dele, porque já temos essa amplitude, sem precisar fazer . Beleza? Então:
Assim, considerando o intervalo de :
Também poderíamos ter: . E agora, como saber qual é o valor correto?
Passo 4
Bom, podemos pensar que a derivada da curva é dada por:
Em , essa derivada é igual a inclinação da reta tangente na curva nesse ponto. Podemos observar que essa inclinação é positiva, logo:
Como , temos que ter:
Logo, só o ângulo de satisfaz essa inequação.
Resposta
Exercício Resolvido #6
PUCRIO-P1-2013.1-Q2
Durante um conserto de uma roda-gigante com raio de metros, um técnico deixa apenas um dos carrinhos instalado. Para testes, a roda é acionada por volta de meio-dia, até atingir uma velocidade angular constante correspondente a uma volta a cada segundos, no sentido anti-horário. O técnico então observou que a sombra do carrinho projetada no chão descreve um movimento harmônico simples. Suponha que o técnico começou a observar a sombra quando o carrinho se encontrava no alto da trajetória. (Adote o ponto central da projeção como origem do eixo e considere que a sombra possui velocidade inicial negativa).
- Encontre a amplitude do movimento da sombra projetada no solo.
- Encontre o período e a frequência angular deste movimento.
- Escreva as equações que descrevem a posição, a velocidade e a aceleração da sombra em função do tempo neste movimento harmônico simples.
- Faça um gráfico da sombra em função do tempo para dois períodos. No gráfico devem estar indicados, numericamente, os valores máximo e mínimo da posição e os tempos em que a sombra atinge esses pontos.
Passo 1
a)
Galera, aqui a gente precisa perceber apenas uma coisa: um MHS pode ser encarado como uma projeção de um MCU.
A figura abaixo ilustra isso:
Tá vendo a linha preta embaixo do círculo? Essa é a representação do MHS.
Bom, com isso, podemos responder a primeira pergunta: qual a amplitude?
Pela figura, percebemos que a amplitude é o raio do círculo.
Então:
Passo 2
b)
Seguindo a mesma idéia de antes, é fácil perceber que o período, frequência e a frequência angular do movimento serão os mesmo que o do MCU.
Então, o período do MHS já está dado no enunciado.
Segundo o enunciado, a roda gigante completa uma volta a cada . Isso quer dizer que o período é justamente esse:
E a frequência angular é:
Passo 3
c)
A posição segue o modelo dos MHS e é dada por:
Já sabemos quase tudo, menos a fase ().
Bom, a informação que temos é que o movimento do carrinho, e de sua sombra, começa quando o carrinho se encontra no ponto mais alto da trajetória. Nesse caso, a projeção da sua sombra se encontra na origem do sistema que descreve o MHS( aquela linha preta lá de cima).
Então, depois de tanto blá blá blá, o que quero dizer é que:
Ou seja:
Show! Então:
Pra achar a velocidade e a aceleração, basta a gente derivar esse equação uma vez e depois derivar de novo:
Passo 4
d)
Basta a gente pegar sucessivos valores de tempo pra formar o gráfico:
Resposta
a)
b)
c)
d)