Introdução ao MHS
Teoria
O que é MHS?
MHS significa Movimento Harmônico Simples.
O que isso quer dizer?
Movimento harmônico é um movimento oscilatório, ou seja, que apresenta algumas propriedades que se repetem com o tempo (como a posição , a velocidade , aceleração , etc).
A estrutura de um movimento harmônico sempre vai ser dada por funções seno ou cossenos (isso que vai gerar as repetições). Por exemplo:
E por que se chama movimento harmônico simples?
Movimento harmônico simples significa que é um movimento harmônico que não tem atrito. Existem ainda os MHAs, que são movimentos harmônicos amortecidos. Mas não se preocupe com eles agora.
Equação do MHS
Como a gente viu, a equação do MHS vai ser ou uma função seno ou uma função cosseno.
No geral, ela vai ter o seguinte formato:
Ou:
Essa é a chamada equação da posição de um MHS.
Nessa equação, temos:
Representa a amplitude do movimento.
Representa a frequência angular.
Representa a fase do movimento.
Mas o que significa cada uma dessas coisas?
Bom, nós vamos entender melhor nos exercícios, mas por ora, basicamente temos o seguinte:
É o maior “afastamento” possível que o objeto que está executando o MHS pode ter da origem.
É uma espécie de velocidade angular. É dada em . A expressão geral pra ela é:
Onde é o período do movimento, ou seja, o tempo de um ciclo total.
A frequência é o inverso do período:
É o ângulo inicial do movimento. Tem a ver com a posição inicial do objeto.
Velocidade e aceleração
E como são as equações da velocidade e da aceleração pros MHS?
Muito simples, basta a gente derivar (:
Derivando uma vez:
Repare que, como o seno varia entre -1 e +1, então temos a velocidade máxima:
E o objeto fica variando entre as velocidades e .
Para a aceleração, derivamos outra vez:
A aceleração máxima é:
Defasagem entre a velocidade e aceleração
Aqui vamos ver que existe uma defasagem entre as funções seno e cosseno.
Exemplo:
Quando , temos que .
Ou quando , temos que .
Isso quer dizer que as funções estão defasadas por .
Isso também vai acontecer com a velocidade e com a aceleração:
- Quando a aceleração for máxima, a velocidade será mínima (zero).
- Quando a velocidade for máxima, a aceleração será mínima (zero).
Posições de velocidade nula e aceleração nula
Vamos tentar descobrir as posições onde a velocidade de um MHS torna-se nula intuitivamente. Veja a figura:
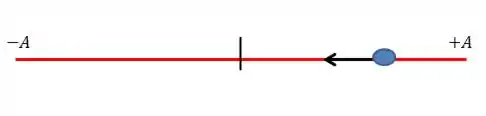
A bolinha azul está se movendo para a esquerda, em MHS, com velocidade não nula. Pra completar o Ciclo do MHS, ela deve chegar até a extremidade esquerda e voltar.
Onde a velocidade se anulará então?
No extremo , pois ali a velocidade muda de sentido.
Isso acontece também pro extremo direito. Então, podemos dizer que:
Show?
Bom, como vimos antes, onde há um mínimo de velocidade há um máximo de aceleração. Assim:
A aceleração será máxima em e .
Vamos analisar de novo o movimento da partícula. Como a velocidade se anula nas extremidades, temos que o valor inicial dela, em , seja 0, e em também. Porém, ela se move nessa trajetória, logo, a partir das extremidades a velocidade tende a crescer.
Onde ocorre o máximo da velocidade?
Em
Pelos motivos que vimos antes, a aceleração se anula em
Olha o resuminho bizu!!!
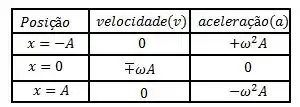
Bora fazer uns exercícios disso aí (:
Velocidade e aceleração
Defasagem entre a velocidade e aceleração
Posições de velocidade nula e aceleração nula
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 107-11
A função: descreve o movimento harmônico simples de um corpo. Em , quais são:
- O deslocamento.
- A velocidade.
- A aceleração.
- A fase do movimento.
- A frequência.
- O período.
Passo 1
Nessa questão, nos foi dado uma função posição para um MHS.
Em alguns itens, iremos usar a fórmula dada para encontrar o deslocamento, a velocidade e a aceleração.
Nos demais itens, iremos comparar a função dada com a fórmula geral e encontrar o que se pede.
A fórmula geral da posição num MHS é:
Aonde,
é a amplitude do movimento.
é a frequência angular.
é a constante de fase.
Passo 2
a)
Para encontrarmos o deslocamento no tempo , precisamos saber qual a posição no tempo e para isso, só precisamos usar a função dada e aplicar o valor :
Por que
Porque :
Isso é uma propriedade trigonométrica:
Toda vez que somamos a um ângulo um número inteiro de voltas(um múltiplo de , como , os senos e cossenos desse ângulo vão ser os mesmos que o do ângulo inicial.
Beleza, mas nós calculamos a posição, certo? Queremos o deslocamento, logo, precisamos descontar desse valor a posição inicial.
E qual é a posição inicial? A posição para
Opa, então o deslocamento será:
Perceba que esse deslocamento é um vetor( no caso calculamos o módulo dele) e por isso é nulo.
Ou seja: O móvel voltou para a posição inicial, mas a informação acima não quer dizer que o móvel não percorreu distâncias.
Passo 3
b)
Primeiro, precisamos derivar a fórmula:
Derivando:
Aplicando para
Passo 4
c)
Novamente, derivando:
Aplicando para
Passo 5
d)
Comparando a fórmula dada, com a fórmula geral:
Da definição, sabemos que a constante de fase é .
Passo 6
e)
Bom, na fórmula existe o valor de . No caso, ela vale:
Assim fica fácil achar o período:
O período vale:
Com isso, a frequência é dada por:
Passo 7
f)
Calculado no item anterior:
Resposta
a)
b)
c)
d)
e)
f)
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 106-2.
Uma partícula com massa de descreve um movimento harmônico simples com um período de e uma velocidade máxima de . Calcule:
(a) a frequência angular.
(b) o deslocamento máximo da partícula.
Passo 1
a)
Basta a gente usar a fórmula do período:
Passo 2
b)
O deslocamento máximo é o valor da amplitude (
Mas nós não sabemos esse valor. Porém, sabemos o valor da velocidade máxima, dada por:
E também sabemos . Assim:
Resposta
a)
b)
Exercício Resolvido #3
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 106-1
Qual é a aceleração máxima de uma plataforma que oscila com uma amplitude de e uma frequência de ?
Passo 1
Opa! Essa é moleza! Basta a gente aplicar:
Ou em módulo:
Passo 2
Achando
Agora é só aplicar mesmo:
Resposta
Exercício Resolvido #4
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 106-5
Um objeto que executa um movimento harmônico simples leva 0,25 s para se deslocar de um ponto de velocidade nula para o ponto seguinte do mesmo tipo. A distância entre esses pontos é 36 cm. Calcule:
(a) o período.
(b) a frequência.
(c) a amplitude do movimento
Passo 1
Bom, nós já sabemos que os pontos de velocidade nula são os pontos das extremidades dos MHS (já que ali a partícula para e muda o sentido de sua velocidade).
Assim, podemos começar a calcular o que se pede.
Passo 2
Bom, como a partícula saiu de um ponto de velocidade nula para o outro, é de se esperar que ela percorreu uma distância
Ou seja, vamos imaginar que ela saiu de e foi pra .
Assim:
E essa é a resposta da letra c).
Passo 3
Quanto ao período:
O tempo decorrido entre a ida de para representa meio período, já que se o móvel fizesse o percurso de volta ele voltaria pra onde tinha saído.
Assim:
E a frequência é o inverso do período, logo:
Resposta
a)
b)
c)
Exercício Resolvido #5
USP-P1-2014-Q8
Uma partícula descreve um movimento harmônico simples de período e amplitude de . O módulo de sua velocidade ao passar por um ponto de trajetória cuja elongação é vale:
Passo 1
Bom, galera, aqui nós vamos usar basicamente as três equações abaixo:
Passo 2
Vamos calcular primeiro o , dado por:
Vamos lá! Nós queremos saber a velocidade pra uma determinada elongação .
Vamos isolar os senos e cossenos das equações anteriores:
E
Agora vamos usar o fato de que:
Resposta
d)