MHS + Colisões
Produzido por Leonardo de BemTeoria
Falaaa aí galerinha bonita, xuxu beleza?! Hoje vamos aprender um pouquinho sobre sistemas onde ocorrem colisões seguidas de um Movimento Harmônico Simples (ou MHS para os mais íntimos).

A gente já viu como se comportam sistemas onde correm colisões normais, elásticas e inelásticas, como por exemplo as bolas de sinuca colidindo elasticamente umas com as outras, ou também um pivete jogando um chiclete que colide inelasticamente e gruda em um motoqueiro. Mas beleza, e agora se a gente tivesse um projétil sendo disparado contra um bloco preso a uma mola, igual na figura abaixo:
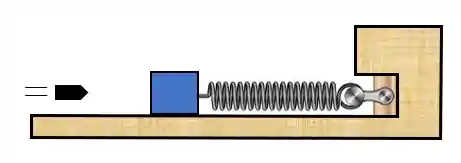
Se o projétil colidisse inelasticamente com o bloco, de maneira que os dois permanecessem juntos após a colisão, como o sistema se comportaria?!

Então calma lá chefia, porque saca só, se o projétil colide com o bloco de forma que os dois permanecem juntos, isso quer dizer que os dois entrarão em movimento unidos com a mesma velocidade e energia cinética , até a mola absorver toda essa energia cinética e transformar em energia potencial elástica , tal que:
Em consequência disso, a energia potencial elástica armazenada na mola, voltará a acelerar o sistema bloco-projétil, só que agora pro outro sentido, de forma que ele passará pelo ponto de equilíbrio, até atingir um ponto simétrico do outro lado do movimento, com a mesma amplitude, logo:
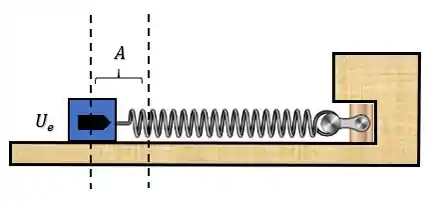
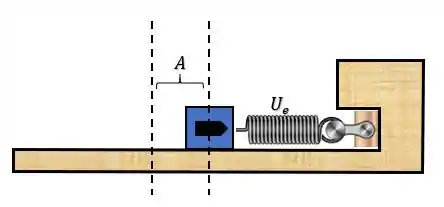
Ou seja, a partir desse ponto, o conjunto bloco-mola, passa oscilar periodicamente, executando um MHS de amplitude .
Belejóia, então nesse caso precisamos saber com que velocidade o conjunto bloco-projétil começa o movimento, e qual a amplitude desse movimento. Ai é que entra nossos dois digníssimos conceitos da física, chamados:
- Conservação do Momento Linear
- Conservação da Energia Mecânica
Bora lá dar uma olhadinha mais de perto neles.
Conservação do momento Linear
Vamos supor que o projétil tenha massa e velocidade , enquanto o bloco possui massa , logo:
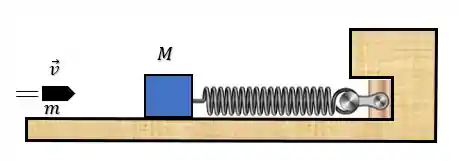
Por convenção, tomamos o sentido para a direita como positivo. Dessa forma, quando os dois colidem, o sistema passa ter a seguinte configuração:
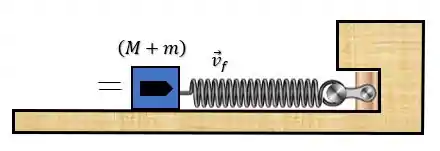
E a malandragem aqui, é que exatamente nesse instante podemos usar a conservação do momento linear para descobrir a velocidade final que o conjunto bloco-projétil assume no início do MHS.

De forma que pela conservação do momento linear, vamos obter que:
Ou seja, o momento linear inicial é igual ao momento linear final , logo:
Sendo assim, isolando :
E assim conseguimos descobrir a velocidade final do conjunto bloco-projétil. Essa é a velocidade que o sistema inicia o MHS.

Conservação da energia e MHS resultante
Belezoca pessoal, agora pra gente descobrir a amplitude desse movimento, podemos usar a conservação da energia mecânica, dada como:
Ou seja, a energia mecânica , é igual a soma da energia cinética com a energia potencial . Agora saca só, no ponto onde a mola está comprimida/esticada o seu máximo, temos uma deformação de tamanho , isso quer dizer que para uma mola de constante elástica , a sua energia mecânica total será:
Já a energia cinética, no ponto onde ela é máxima, teremos que:
A malandragem agora, é que nesse momento, quando a energia cinética é máxima, a energia potencial elástica é mínima, afinal a mola está em seu estado mais relaxado. Sendo assim, nesse momento, teremos que:
Logo:
Portanto, isolando amplitude do MHS, teremos que:
E o legal disso tudo, é que podemos lembrar lá dos termos do MHS, como por exemplo a frequência angular . Em um sistema massa-mola, de constante elástica e massa , a frequência angular é dada como:
Então na nossa equação para a amplitude, o termo , é o inverso da frequência angular do sistema:
Tal que:

Maaaaas, também podemos expressar a amplitude em termos da velocidade inicial , se a gente substituir o valor de na equação inicial, teremos que:
Logo:
Ou seja, se a gente possuir somente o valor das massas, da velocidade inicial e da constante elástica da mola, conseguiremos determinar a velocidade final e a amplitude do MHS. Além disso, ainda podemos relacionar essas grandezas com alguns termos do MHS como a frequência angular .
Show de bolinhas pessoal?! Então bora lá fazer uns exercícios sobre isso pra ver se a gente é ASTRONAUTA mesmo.

Conservação do momento Linear
Conservação da energia e MHS resultante
Exercícios Resolvidos
Exercício Resolvido #1
Um bloco de massa , em repouso numa mesa horizontal sem atrito, é ligado a um suporte rígido por duas molas de constante elástica e , de modo que . Uma bala bala Juquinha, de preferência... pra quê falar de mais violência ![]()
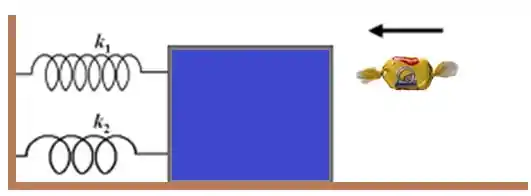
De posse dessas informações, determine a velocidade do conjunto imediatamente após a colisão e a amplitude do movimento harmônico simples associado.
(Obs.: Dica do Dexter ![]() – Confira o nosso material de associação de molas)
– Confira o nosso material de associação de molas)
Passo 1
Beleza....Vamos resolver logo essa parte da velocidade que é de boas....Vamos relembrar a conservação de momento linear para colisões que vimos lááá nas priscas eras de Física 1.
Antes da colisão, a bala Juquinha tinha velocidade e o bloco tinha velocidade nula, logo, o momento linear inicial é:
Após a colisão, tanto o bloco quanto a bala Juquinha se deslocam com a mesma velocidade
Como :
E essa é a velocidade do conjunto logo após a colisão!
Passo 2
Show de bola! Já calculamos a velocidade linear do conjunto logo após a colisão. Precisamos calcular agora qual será a amplitude do movimento oscilatório do conjunto. E aí??? Será que deu ruim??? ![]()
Sabe como vamos resolver esse problema, jovem padawan? Usando a Força? (Quem pegou a referência de Star Wars aí?)

Mais do que isso! Usaremos a Energia! Bom, mais precisamente a conservação dela ![]() .
.

Vamos considerar como início do movimento o momento em que a bala atinge o bloco. Nesse momento, a mola ainda não se comprimiu, certo? Looogo, a energia mecânica é só a energia cinética “recém-adquirida” pela colisão da bala:
Bom, e depois? Depois disso, o bloco vai comprimir a mola pouco a pouco, até que essa atinja uma compressão máxima. Essa compressão máxima será a amplitude do movimento
Belezinha... Assim, no final das contas (estamos chegando no final delas mesmo), a energia mecânica vai ser puramente energia potencial elástica:
Opa... Dexter mandou lembrar que .
Bom, como a energia se conserva, a energia mecânica inicial será igual à energia mecânica final:
Resposta
;
Exercício Resolvido #2
Imagine um experimento em que temos um carrinho de massa , inicialmente em repouso, preso a uma mola relaxada de constante elástica e que pode se deslocar sem atrito sobre uma mesa horizontal. Nesse experimento, um carrinho de massa se aproxima com uma velocidade e colide frontalmente com o primeiro carrinho. Após a colisão, que é completamente inelástica, os carrinhos passam a oscilar juntos.
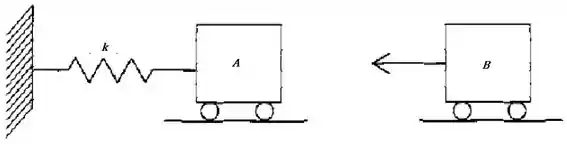
Calcule a velocidade dos blocos logo após a colisão, a frequência angular de oscilação e a amplitude, , do movimento.
Passo 1
Bom, num primeiro momento a gente precisa se lembrar de um conceito lááá de Física 1...Lembra da conservação de momento linear? O quêêê??? Não se lembra??? Td bem, o Responde Aí está aqui pra isso ![]()

Se nós voltarmos lá nos nossos assuntos de Conservação do Momento Linear e de Colisões, vamos ver que:
Passo 2
Para calcularmos a frequência angular de oscilação, basta nos lembrarmos que
Reparou no ali? Ele será a soma das massas dos dois carrinhos, ou seja, . Aí ficou fácil, né?
Show de bolinhas! Agora só falta calcular a Amplitude!!!
Bom...nós vamos matar isso por energia. ![]()
Nós temos a velocidade máxima dos blocos, pois é aquela que eles têm logo após o impacto.
Então temos a energia cinética máxima. Basta a gente descobrir qual é a energia potencial máxima para descobrirmos a amplitude, pois:
E a energia cinética é:
E isso é igual a :
Resposta
Exercício Resolvido #3
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 107-14.
A figura abaixo mostra o bloco 1, de massa , deslizando para a direta, sobre uma superfície elevada, com uma velocidade de s. O bloco sofre uma colisão elástica com o bloco 2, inicialmente em repouso, que está preso a uma mola de constante elástica (Suponha que a mola não afete a colisão.) Após a colisão, o bloco 2 inicia um MHS com um período de e o bloco 1 desliza para fora da extremidade oposta da superfície elevada, indo cair a uma distância horizontal de dessa superfície, depois de descer uma distância de . Qual é o valor de ?
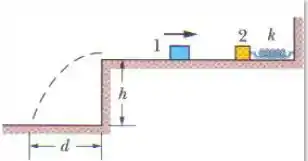
Passo 1
Bom, primeiro vamos dar uma resumida nesse enunciado aí! =p
De início, temos uma colisão elástica entre as massas 1 e 2, ambas sobre a superfície elevada. Depois disso, a massa 2 entra em MHS, enquanto a massa 1 cai da superfície elevada, percorrendo uma distancia horizontal , que é o que queremos achar.
Passo 2
Como o enunciado disse que a mola não afeta a colisão, nós podemos usar as fórmulas que nos dão as velocidades em uma colisão elástica.
Porém, antes disso, vamos achar a massa do bloco 2.
Como temos a frequência com que ele oscila após a colisão a e constante da mola, podemos fazer:
Só basta a gente calcular
Assim:
Passo 3
Agora vamos escrever a equação da conservação do momento pra essa colisão:
Além dessa, temos a equação da conservação da energia:
Show?? Temos duas incógnitas ali: (velocidades dos blocos após a colisão).
Vamos resolver o sistema acima, isolando na primeira equação e substituindo na segunda
Assim, na segunda equação fica
Agora, vamos fazer as contas e achar . Podemos já substituir e os valores das massas, também.
Abrindo esse produto notável
Chegando na equação
Temos as duas raízes e . Mas se valesse , isso implicaria que o bloco teria uma velocidade nula, o que sabemos, pelo enunciado, que não é verdade.
Excluindo a raiz negativa, encontramos pra
Passo 4
Agora é só cinemática!!!! Essa velocidade, , vai ser a velocidade do bloquinho 1 após a colisão. Como ele vai cair da mesa, essa vai ser a velocidade inicial do lançamento oblíquo.
Então, pra achar o alcance, vamos usar:
Onde é o tempo de queda. E como se calcula ele mesmo? Lembrando das fórmulas de lançamento oblíquo, a gente pode escrever:
Aplicando o valor da altura do enunciado:
Assim:
Resposta
Exercício Resolvido #4
PUCRIO-P1-2013.2-Q2
Um bloco de é unido a uma mola e colocado em uma superfície horizontal sem atrito. Uma força horizontal de é necessária para manter o bloco em repouso quando é puxado de de sua posição de equilíbrio. O bloco é liberado do repouso a partir deste ponto e realiza um movimento harmônico simples.
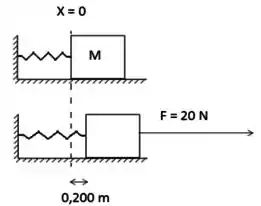
- Encontre a constante de força da mola e a frequência de oscilação.
- Determine a energia cinética máxima do bloco.
- Considere agora que o bloco esteja em repouso na sua posição de equilíbrio e um projétil de massa com velocidade de atinge o bloco, como mostra a figura (a) abaixo. O projétil fica preso no bloco, como mostrado na figura (b), e o sistema bloco+projétil passa a oscilar num movimento harmônico simples. Determine a amplitude do MHS resultante.
- Se o projétil do item c) atingir o bloco quando este se encontra com velocidade nula na posição , qual será a nova amplitude do movimento?
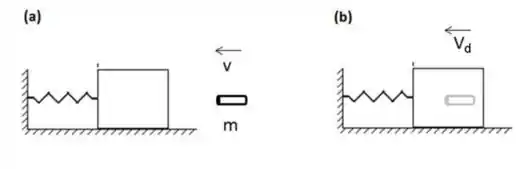
Passo 1
Bora lá! Primeiramente temos um sistema massa-mola que começará a entrar em MHS, após ter sido afastado de da sua posição de equilíbrio. Queremos encontrar algumas informações sobre o MHS que ele realiza. Depois, vamos considerar que ocorre uma colisão entre esse bloco e um projétil que fica preso nele.
Passo 2
a)
Aqui queremos encontrar a constante de força da mola e a frequência de oscilação.
O enunciado te deu o da mola e a força gerada por ela, então, para calcular a constante:
E a frequência angular é dada por:
A frequência de oscilação será:
Passo 3
b)
A energia cinética máxima ocorre quando toda a energia mecânica é cinética. Ou seja:
E a energia mecânica máxima é dada por:
Onde é a amplitude do movimento.
E qual a amplitude do movimento? Nesse caso, vale:
Então:
Então:
Passo 4
c)
Bom, galera, aqui vamos lembrar um pouco do que sabemos sobre colisões.
Como o sistema é isolado de forças externas, podemos dizer que o momento se conserva e então:
Então:
Essa é a velocidade do conjunto corpo mais bloco.
Beleza, mas e aí? Não queremos isso. Queremos saber é qual a amplitude do MHS.
Basta a gente lembrar que a energia cinética máxima é igual a , então:
Calculando
Então, usando a equação anterior:
Passo 5
d)
Após o choque, a velocidade continua a mesma que a do item c), só que agora temos também energia potencial. Então:
Resposta
a)
b)
c)
d)
Exercício Resolvido #5
PUCRIO-P1-2014.1-Q2
Um carrinho de massa , inicialmente em repouso no ponto , está preso a uma mola relaxada de constante elástica e pode se deslocar sem atrito sobre uma mesa horizontal. Um carrinho de massa se aproxima com uma velocidade e colide frontalmente com o carrinho . Após a colisão, que é completamente inelástica, os carrinhos passam a oscilar juntos. Encontre, em função dos dados acima,
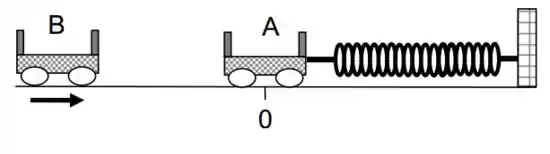
- A velocidade dos blocos logo após a colisão.
- A frequência angular de oscilação e a amplitude, , do movimento.
- Considerando o instante de choque, obtenha a constante de fase e escreva a posição em função do tempo,
- Suponha que ao atingir a posição o carrinho se solte do sistema. Encontre a nova velocidade do carrinho ao passar pelo ponto
Passo 1
a)
Bem, aqui a gente só precisa lembrar da conservação de momento linear em colisões. Se tiver alguma dúvida, dê uma olhada lá no nosso guia de colisões.
Passo 2
b)
Vamos precisar também lembrar dos conceitos de energia. Nós temos a velocidade máxima dos blocos, pois é aquela que eles têm logo após o impacto.
Então temos a energia cinética máxima. Sabemos que essa energia cinética máxima é igual à energia potencial máxima:
E a energia cinética é:
Assim:
E a frequência angular é facilmente achada usando-se a fórmula:
Passo 3
c)
A função é a função que nos dá a posição de um MHS, então ela tema a forma:
Temos todas as informações, menos a . Só que pelo enunciado, em , . Então:
Ou seja, um múltiplo ímpar de
Vamos analisar o sinal da velocidade em pra saber mais da constante de fase:
Em
ou
Então:
Ou
Com e dados na letra b.
Passo 4
d)
Quando o carrinho se solta em , a energia mecânica se conserva.
Isso quer dizer que vamos ter que calcular a energia mecânica naquele ponto e depois calcular ela no ponto , onde a velocidade é máxima. Assim, lembrando que a massa do sistema diminuiu, podemos escrever:
Então:
Resposta
a)
b)
c)
d)