Pêndulos Simples
Produzido por Leonardo de BemTeoria
Vamos aprender aqui o que é um pêndulo simples e como chegar em algumas equações que regem esse tipo de movimento:
O que é um pêndulo simples?
Um Pêndulo simples tem o seguinte formato padrão:
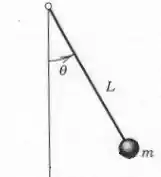
Pra se chegar na EDO desse movimento, vamos seguir os passos abaixo:
Passo 1: diagrama de corpo livre e forças atuantes.
Isolando a massa, temos o seguinte:
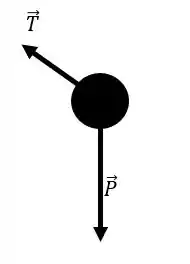
Passo 2: encontrar força resultante.
Como não há movimento na direção do fio, podemos decompor o peso nessa direção e na direção do movimento, perpendicular.
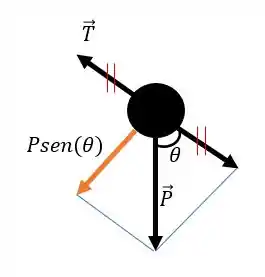
Então a força resultante é dada por:
Passo 3: aplicar a Segunda Lei de Newton para rotações:
é o comprimento do fio e também a distância da massa até o centro de rotação e é o cara que faz o pendulo rotacionar! Repara que é perpendicular ao fio!
Esse sinal de menos vem do fato de que o torque vai sempre querer levar a massa pra posição mais baixa (quando o fio ficar vertical).
Por outro lado, a segunda lei para rotações diz que
Assim
Só que
E o momento de inércia da massa em relação ao eixo de rotação é .
Esse seno tá atrapalhando nossa vida, não é?
Mas para pequenos valores de :
Observação: apareceu um seno, só falar que o ângulo é pequeno e substitui o seno pelo próprio ângulo.
Então:
E aí sim vamos chegar na equação do MHS:
Comparando com a equação do MHS:
Então:
Assim, o período vai ser dado por:
E é essa última equação a mais importante pra você. O período vai variar somente com o comprimento e com a gravidade do local.
A solução dessa EDO é a mesma do MHS
E aí é só brincar pra tirar outras informações como velocidade e etc!
Partiu exercícios? o/
Passo 2: encontrar força resultante.
Passo 3: aplicar a Segunda Lei de Newton para rotações:
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-P2-2014.2-Q8
Marque a alternativa ERRADA a respeito do comportamento de um pêndulo simples, na aproximação de pequenos ângulos.
- Se dobrarmos o comprimento da corda do pêndulo, o seu período também vai dobrar.
- O período não depende das condições iniciais.
- A velocidade máxima de oscilação não depende do valor da massa do pêndulo.
- Um mesmo pêndulo na lua oscila com menor frequência do que na terra sob as mesmas condições iniciais.
Passo 1
Vamos analisar uma por uma:
a)
Na nossa teoria, nós vimos que a frequência angular de um pêndulo simples é dada por:
Sendo , temos que
Agora, se duplicarmos o comprimento do pêndulo, ou seja, , teremos:
Então na verdade não duplica o período. Ele só aumenta por um fator de .
Então essa é a errada.
Passo 2
b)
De fato, não depende. A gente acabou de calcular ele em a), e não usamos condições iniciais, só valor da frequência angular.
c)
Pra encontramos o valor da velocidade máxima, a precisamos montar a expressão pra oscilação do MHS do pêndulo. A gente fez isso na teoria, A expressão é parecida com a de um MHS normal, só trocamos por
A velocidade máxima vai ser o valor máximo da derivada disso ai. Só que com essa expressão não depende da massa, a sua derivada também não dependerá, assim como o seu valor máximo.
Logo, está correto.
d)
Sendo o período dado por:
A frequência, que é o inverso do período, será dada por:
Ou seja, se a gravidade de um local for maior que a do outro, ali o pêndulo oscilará com uma frequência maior. Logo, como a gravidade da lua é menor que a da Terra, lá o pêndulo terá uma frequência menor.
Item correto.
Resposta
a)
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 15, pp 111-75.
Qual a frequência de um pêndulo simples de de comprimento:
- Em uma sala.
- Em um elevador acelerando pra cima a
- Em queda livre.
Passo 1
Bom, única coisa que você vai precisar pensar é na aceleração resultante a qual o pêndulo esta submetido.
a)
Em uma sala, apenas existe a aceleração da gravidade. Assim:
Passo 2
b)
Quando o elevador acelera pra cima, o pêndulo sofre uma aceleração extra pra baixo de mesmo valor.
Assim:
Aqui você poderia se perguntar: mas como o elevador tá acelerando pra cima, eu não deveria subtrair essa aceleração da gravidade? E a resposta é... NÃO. Por que não? Porque quando o elevador tá fazendo força pra cima, o pêndulo tá fazendo uma força de reação pra baixo.
É só você se imaginar no elevador: quando ele começa a subir não dá impressão de que você fica mais pesadx? É isso.
Passo 3
c)
Quando o móvel está em queda livre, o fio do pêndulo fica frouxo. (é o mesmo efeito que acontece com nossos pés, que tendem a se desprenderem do chão).
Assim, não podemos calcular a frequência nesse caso.
Resposta
a)
b)
c)
Não podemos calcular nesse caso.
Exercício Resolvido #3
UFRJ-P2-2014.1-M07
Dois pêndulos de comprimentos e oscilam de tal modo que os dois pesos em suas extremidades aproximam-se, sem se tocar, sempre que decorrem seis períodos do pendulo menor e quatro períodos do pendulo maior. Qual relação ?
Passo 1
Sabemos que para um pendulo
Sabemos que
Então
Passo 2
Pelo enunciado
vamos ter
Elevando ao quadrado
Resposta
Letra A
Exercício Resolvido #4
Em que ponto do movimento de um pêndulo simples a tração no fio atinge o valor máximo? E o valor mínimo?
Passo 1
Lembra do pêndulo simples? É esse camarada aqui:
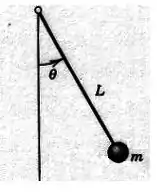
E como as forças se decompõem? Dá uma olhada nessa figura:
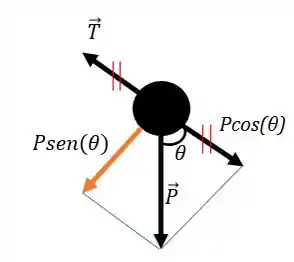
E como não tem movimento na direção do fio, podemos dizer que:
Passo 2
Bom, se a tração é proporcional ao cosseno do ângulo, quando ela vai ser máxima? Quando o cosseno for máximo né, ou seja, quando:
Então a tração vai ser máxima quando for igual a zero, ou seja, quando o pêndulo estiver na posição vertical.
Passo 3
Usando o mesmo raciocínio, quando a tração vai ser mínima? Quando o cosseno for mínimo também!
Lembrando que o cosseno é decrescente no primeiro quadrante (ou seja, de zero a 90 graus, quanto maior o ângulo menor o cosseno) o cosseno vai ser mínimo quando for máximo!
O ângulo máximo é sempre o ângulo da posição em que o pêndulo foi abandonado.
“Mas como eu acho esse ângulo?”
Então, o problema pode te dar a posição usando e não x, tipo assim:
E aí no caso o seu ângulo máximo vai ser .
Entãããooo....ele pode te dar a altura h de onde o pêndulo foi abandonado, tipo assim:
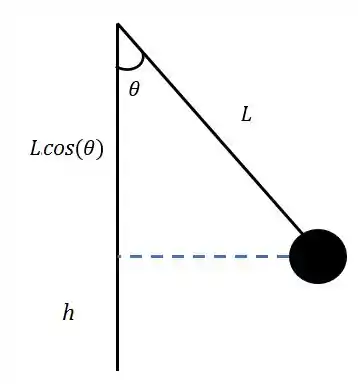
Nesse caso você vai usar a relação:
Passo 4
Resumindo, tração máxima:
Tração mínima:
Resposta
Tração máxima:
Tração mínima:
Exercício Resolvido #5
A Figura mostra um pêndulo de comprimento com uma bolinha de massa . A bolinha é presa a uma mola de constante de força , como mostrado. Quando a bolinha está diretamente abaixo do suporte do pêndulo, a mola está frouxa.
Seja o ângulo entre a haste a vertical. Para muito pequeno:
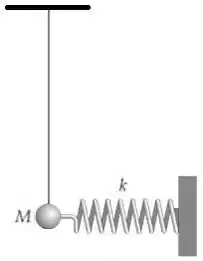
Calcule o período do pendulo.
Passo 1
Bom, vamos lá...Vamos começar fazendo um esboço de diagrama de corpo livre para identificarmos as forças que agem no sistema.
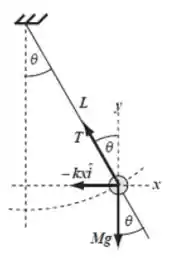
Pela figura, vemos que as forças que agem na direção horizontal são:
Quanto vale a tensão? Podemos descobrir isso fazendo o equilíbrio vertical das forças:
Assim, na primeira equação:
Como para pequenos ângulos:
E do enunciado:
E:
Assim:
Passo 2
Opa! Essa é uma EDO no formato que nós conhecemos! Looogo,