Introdução a Ondas Sonoras
Produzido por Leonardo de BemTeoria
Introdução a Ondas Sonoras
O que é uma onda sonora?
A onda sonora é definida como um tipo de propagação de energia através de um meio por meio de compressão e descompressão adiabática.
Tá, mas até aqui estamos falando grego certo?
Vamos compreender pensando numa situação, imagina que temos um alto falante num meio de moléculas de ar comum, dispersas e resolvemos liga-lo. O que vai acontecer com as moléculas após o alto falante ser ligado?
Algo mais ou menos assim:
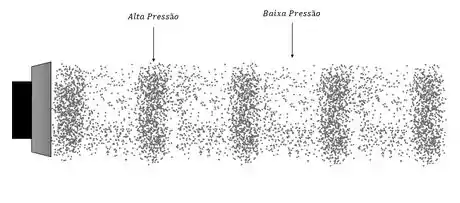
As moléculas que antes estariam dispersas agora vão se deslocar, e formar zonas de baixa pressão nos picos de deslocamento. Onde não houver deslocamento ou pouco deslocamento as moléculas vão se comprimir em zonas de alta pressão.
Essa onda mostrada é uma onda longitudinal e mecânica.
Onde uma onda longitudinal é aquela em que a direção de propagação é a mesma direção de oscilações do meio.
E ser uma onda mecânica significa que ela tem necessidade de um meio para propagar!
Por isso, as ondas sonoras são ondas de pressão e ondas de deslocamento, pois exercem uma pressão e o meio se desloca à medida que a onda se propaga.
Tá beleza, mas e aí, como vamos calcular esse tipo de onda?
Módulo de compressibilidade a velocidade do som
Existem alguns parâmetros que precisamos conhecer antes de partirmos pros cálculos e dois deles são o módulo de compressibilidade e a velocidade do som.
O módulo de compressibilidade é o que mede se um gás pode ser muito ou pouco comprimido.
Quando o gás pode ser muito comprimido, o módulo de compressibilidade é baixo, e quando pode ser pouco comprimido, é alto.
O módulo de compressibilidade é representado pela letra Ele pode ser calculado por:
Onde é a densidade do gás e a velocidade do som.
Daí tiramos que a velocidade do som pode ser calculada assim:
A velocidade do som no ar é uma constante que tem módulo de valor:
E se essa velocidade for superada, o que acontece?
Velocidade supersônica
Você já deve ter ouvido falar nisso, certo? Existem jatos que voam com velocidades supersônicas, que é quando se ultrapassa a velocidade do som em um meio.
Quando um objeto se desloca a uma velocidade superior a essa (velocidade supersônica), ele rompe a barreira do som e ocorre um estampido ou estalo.
Ondas Progressivas
Mas como é que eu escreveria uma onda sonora?
Ah, som é uma onda, então o som também deve ter uma função do tipo abaixo que o descreva, certo?
Vamos entender um pouco de como funciona uma onda sonora matematicamente.
Vamos fazer isso analisando os deslocamentos e variações de pressão associados a uma onda sonora que se propaga no ar. Beleza? Vamos lá!
Função de deslocamento
A função que descreve o deslocamento de uma onda sonora é bem parecida com a função que aprendemos para uma onda qualquer.
Essa função é:
Sendo:
Obs: O deslocamento pode ser dado como função seno também, mas por convenção usaremos a função cosseno, beleza?
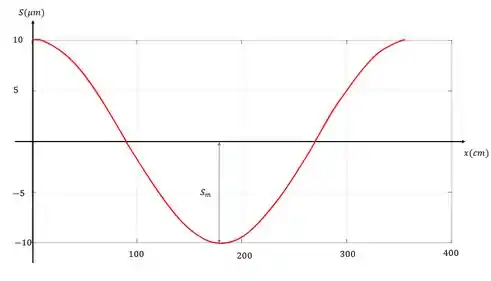
Vamos dar uma olhada num gráfico desse tipo de função para as seguintes condições:
Ou seja:
Teríamos algo do tipo:
Função da variação de pressão
Bom, as ondas de pressão são funções que indicam a variação de pressão de um gás com o passar do tempo.
Essas funções têm uma ligação com a função deslocamento da onda sonora e se relacionam por:
Vamos derivar a expressão de que vimos antes e reescrever essa acima:
é o módulo de compressibilidade e vale:
E reescrevendo a equação ela fica da seguinte forma:
Onde
. Podemos substituir por e chegamos a:
E enfim a equação da variação de pressão fica:
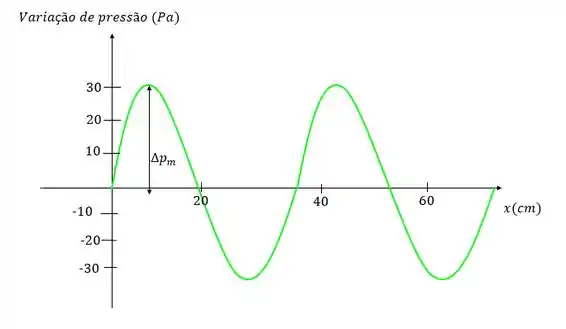
Se liga em como é o gráfico, pra um exemplo onde e temos
Lembrando que todas as relações que usamos para ondas, valem nas ondas sonoras também!! Afinal, elas continuam sendo ondas, não vamos excluí-las só por serem sonoras né?
Pra fixar tudo o que foi visto vamos calcular a velocidade pra onda abaixo, e também a variação máxima de pressão se essa onda se propaga no ar.
Após isso vamos esboçar o gráfico da variação de pressão e da posição e compará-los.
Bom, comparando com o que vimos logo ali em cima na função deslocamento de uma onda, da equação a gente tira que:
Com isso, sabemos que em uma onda vale:
Para achar o valor de :
Para achar o valor de :
Agora é só substituir na fórmula da velocidade:
E a variação de pressão dessa onda é dada por:
Onde
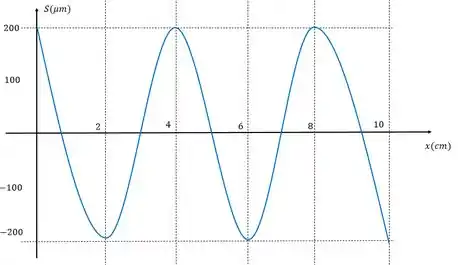
Beleza, agora é só esboçarmos os dois gráficos para e compará-los. Vamos esboçar o gráfico para um valor de de 0 até , e observar o comportamento.
A função deslocamento fica:
Vamos converter a escala da amplitude pra e assim a comparação será numa escala mais compatível:
Pra esboçar esse gráfico é bem tranquilo, é só calcular a função para e após isso repetir o movimento pois aí teremos os múltiplos de e .
Os cálculos da trigonométrica serão feitos em radianos.
Daí o gráfico fica com essa cara:
E o gráfico da variação de pressão, como vai ficar para
Primeiro a gente pega a equação com a amplitude encontrada.
Substituindo o valor e fazendo :
E aqui os pontos importantes são os quais onde o seno dá ou e para esses pontos analisaremos os valores de e :
E o gráfico fica desse jeito:
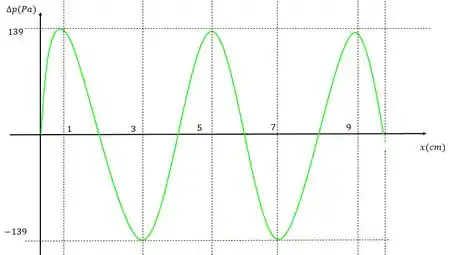
Comparando os dois gráficos temos:
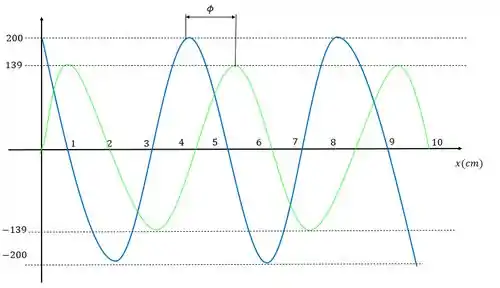
Esse que apareceu é a diferença de fase entre as duas ondas, podemos reescrever a função da variação de pressão como um cosseno também, mas considerando essa diferença de fase entre as ondas.
Repara que o gráfico azul da posição tem maior amplitude nessa escala portanto é aumentado em relação ao gráfico da diferença de pressão.
Agora é partir pra prática!