Interferência de Ondas Sonoras
Teoria
Introdução
Assim como as ondas transversais, as ondas sonoras também sofrem interferência.
Se a gente colocasse dois aparelhos de som, um no ponto e outro no ponto , o que aconteceria no ponto da figura abaixo?
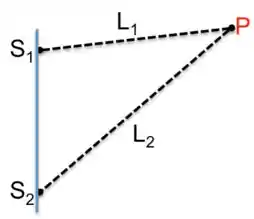
A propagação das ondas sonoras causaria interferência no ponto , e existem dois casos importantes pra gente analisar.
Quando as ondas chegam no ponto em fase e quando as ondas chegam num ponto em fases diferentes.
Interferência Construtiva
O primeiro caso é quando as ondas saem em fase e chegam em fase no ponto P.
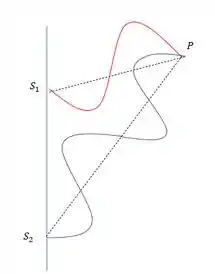
Se colocarmos essas ondas alinhadas vamos poder perceber o seguinte:
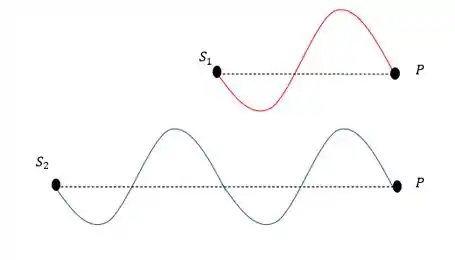
Nesse caso as ondas saem da mesma posição e chegam no ponto da mesma forma, num mínimo.
Quando as ondas chegam no ponto com o mesmo comportamento, dizemos que elas chegam em fase, e a interferência naquele ponto , é uma interferência construtiva.
Podemos perceber, que a onda que sai de , percorre um caminho menor, em relação a onda que sai de . Pra gente ver isso melhor basta contarmos quantos comprimentos de onda temos em cada percurso.
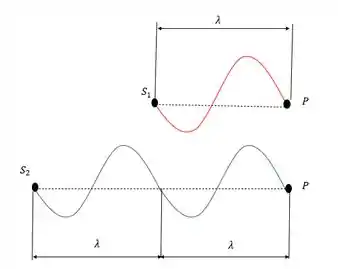
Então com isso temos:
E pra interferência construtiva a diferença de caminho tem sempre que ter um resultado inteiro de comprimento de onda.
Num caso geral pra interferência construtiva.
Onde
Interferência Destrutiva
O segundo caso é quando as ondas chegam de forma diferente no ponto , dá uma olhada na figura.
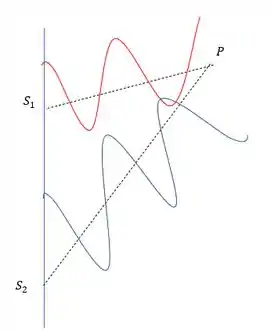
Se colocarmos as ondas alinhadas vamos poder analisar melhor o que acontece ali, mas de cara a gente já vê que elas não chegam na mesma fase.
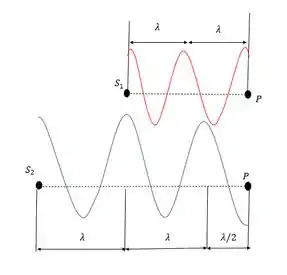
E aqui a gente pode ver que uma onda chegou com a amplitude máxima e a outra com amplitude mínima. Quando as ondas chegam desse jeito no ponto ocorre a interferência destrutiva.
No geral como é a diferença de caminho da interferência construtiva? Bom vamos descobrir, pela figura sabemos que:
Então:
Opa deu um valor quebrado de , e é isso mesmo! No caso da interferência destrutiva a diferença de caminho no geral vai ser um múltiplo de .
Onde
Diferença de fase
Pra gente entender a diferença de fase é fundamental termos fixado a diferença de caminho. Então o que é a diferença de fase?
Vamos aprender olhando essas duas equações de onda, você vê algo diferente entre elas?
Esse que aparece na segunda onda é a diferença de fase ela é responsável por fazer a onda chegar em fase diferente num determinado ponto, se liga nesse gráfico comparando as ondas.
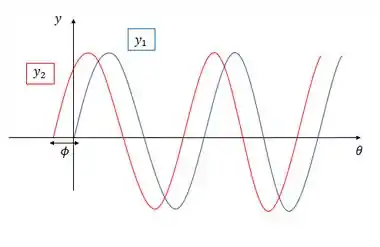
Onde .
Se você somar uma fase qualquer vai adiantar a função seno, por exemplo se no ponto a função de onda tem valor .
Tá, mas qual é a relação da diferença de fase com o comprimento de onda?
Bom se pensarmos que a cada a onda completa um comprimento , podemos dizer que pra um comprimento de onda o ângulo será a diferença de fase .
Rearrumando temos:
Para termos interferência totalmente construtiva, precisamos que a diferença de fase seja nula, ou um múltiplo inteiro de . Sob essas condições, temos que as interferências totalmente construtivas ocorrem sempre que:
Vamos fazer um teste com as nossas equações de onda para , bora somar as duas ondas no ponto.
Como
E se liga:
Então:
E aqui temos a equação que mostra a interferência construtiva dessas ondas:
No ponto onde teremos a amplitude máxima e a interferência construtiva vai resultar:
Graficamente a interferência construtiva dessas ondas que possuem diferença de fase pode ser resumida nessa imagem.
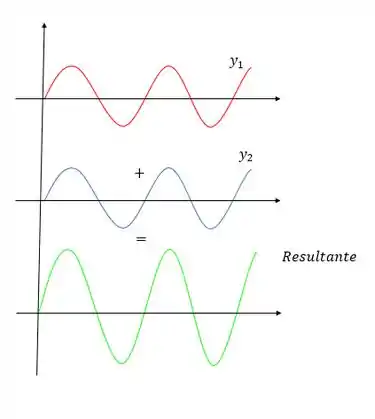
Se a interferência construtiva acontece pra múltiplos de a destrutiva vai acontecer pra múltiplos de que não sejam múltiplos de , mas porquê?
A interferência totalmente destrutiva no ponto ocorre quando as ondas chegam totalmente opostas, e pra mudarmos o sinal de uma função seno basta somarmos ao seu argumento.
Sendo assim para que tenhamos um múltiplo impar de basta somarmos ao
Rearrumando vai ficar:
Sempre será múltiplo de um ímpar de
Se pegarmos a equação das ondas pra um múltiplo a diferença de fase aqui seria dada por:
Vamos pegar a nossa equação da interferência das ondas em
E substituir a diferença de fase:
Teremos o seguinte:
Resumindo, sendo um número inteiro:
Depois de alguns exercícios isso aí vai estar no sangue. Bora praticar!
Interferência Destrutiva
Diferença de fase
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 16
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, , se propagam na mesma direção e no mesmo sentido a . As fontes estão em fase. Qual é a diferença de fase das ondas em um ponto que está a de uma fonte e a da outra?
Passo 1
Temos aqui a seguinte estrutura:
Sabemos que:
E também:
Então:
E, substituindo na primeira, usando igual a , temos:
Resposta
Exercício Resolvido #2
UNICAMP-Questão 3 - P2.2012
Uma onda sonora com comprimento de onda de propaga-se para a direita num tubo que possui uma bifurcação (vide figura). Ao chegar à bifurcação a onda se divide em duas partes. Uma propaga-se em um tubo em forma de semicircunferência, e a outra se propaga em um tubo retilíneo. As duas ondas combinam-se mais adiante, antes de chegarem ao detector. Qual é o menor raio da semicircunferência para o qual a intensidade medida pelo detector é mínima? Se necessário, use .
Passo 1
Bom galera, vamos primeiro identificar do que se trata o problema:
Bem, como queremos saber uma condição para que a intensidade da combinação de duas frentes de ondas seja mínima, estamos lidando com interferência.
E qual o tipo de interferência que o enunciado pede? Como ele quer uma intensidade resultante mínima, a interferência só pode ser destrutiva, afinal, numa interferência construtiva a intensidade das frentes de onda é máxima, já que elas se somam.
Pela nossa teoria, a equação que vamos usar é:
Onde:
Ou seja, a fase é um múltiplo ímpar de .
Passo 2
Vamos por a mão na massa:
Bom, a onda se divide em duas: uma que segue pela semicircunferência e outra que vai pela parte de baixo da mesma.
O comprimento da semicircunferência é a metade do que teria o círculo de raio , ou seja:
Já embaixo, a onda percorre um caminho que equivale a :
Logo:
Pra usar a equação que vimos ali em cima basta saber o valor do comprimento da onda. Opa! Ele já disse isso: . Logo:
Passo 3
Vamos analisar o resultado agora:
Para que a interferência seja destrutiva, é preciso que a diferença de fase seja um múltiplo ímpar de e, além disso, como queremos o menor raio que gere esse efeito, precisamos, também, do menor múltiplo ímpar de
Quem é o menor múltiplo de Ora, o próprio
Logo:
Pronto (:
Resposta
Exercício Resolvido #3
Halliday, David, Fundamentos de física, volume 2: ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 68.
Você está parado diretamente à frente de um dos dois alto-falantes mostrados na figura. Eles estão afastados por de distância e emitem, em fase, um tom de . À medida que você se afasta perpendicularmente ao alto-falante, a que distâncias do alto-falante você escuta um mínimo de intensidade sonora? A temperatura ambiente é .
Passo 1
Quando temos uma questão pedindo máximos ou mínimos, temos que usar as equações de interferência, no caso de interferência destrutiva, temos:
Vamos começar determinando o comprimento de onda . Temos que e , portanto:
Passo 2
Agora que temos o valor de , vamos determinar para que valores de temos mínimos:
Substituindo os valores, temos:
Temos então que os mínimos ocorrem para:
ou ainda
Passo 3
Vamos agora determinar para a situação inicial, para sabermos qual será o próximo mínimo!
Logo, o próximo mínimo ocorre para , pois, podemos ver que diminui à medida que o ouvinte se afasta do auto-falante. Uma boa forma de ver isso é pensando no limite em que a distância é grande, nesse caso, temos que o ouvinte está praticamente à mesma distância dos dois alto falantes.
Seja a distância entre o ouvinte e o alto falante que está na sua frente, temos:
Fazendo o mesmo mimimi para os próximos mínimos, temos:
Resposta
Exercício Resolvido #4
UNICAMP-Questão 4 - P2.2010 – letras a,b
Na figura abaixo dois alto-falantes, separados por uma distância de emitem ondas sonoras em fase. Suponha que as amplitudes do som vindo dos alto-falante são aproximadamente as mesmas na posição de um ouvinte, que está a em linha reta em frente de um dos alto-falantes.
- Para que frequências na faixa de a o ouvinte escutará um sinal máximo?
- Para que frequências nesta faixa ele escutará um sinal mínimo?
Dado:
Passo 1
a)
Bom, galera, nessa questão nós vamos analisar como a diferença dos percursos que as duas ondas sonoras tomam influencia na frequência da onda resultante.
Bora então!
Bem, a onda sonora do alto-falante de cima vai percorrer quantos metros até atingir o ouvinte?
A resposta é simples: como a onda se propaga em linha reta, ela vai percorrer a hipotenusa do triângulo retângulo da figura. Então:
E a outra onda vai por baixo, logo:
Então a diferença de percurso é:
Passo 2
Agora nós vamos usar a fórmula da interferência que vimos na teoria:
Onde é diferença de fase das duas ondas.
Bom, se a diferença de fase é múltiplo de , ocorre uma interferência construtiva e a frequência é máxima na onda resultante (:.
Vamos analisar essa situação:
Logo:
Show!
Bem, mas o que a gente quer saber são as frequências que cabem em uma determinada faixa, né?
Então vamos substituir a frequência nessa bagaça:
Sendo
Ok! Quase tudo pronto! Agora precisamos saber os valores de que estão entre e :
Para
Na faixa!
Na faixa!
Na faixa!
Pra valores maiores de a frequência ultrapassa .
Então as frequências que estão entre e para as quais o ouvinte escutará um sinal de máximo são: e
Passo 3
b)
O raciocínio aqui vai ser quase o mesmo que o do item anterior, só que como agora queremos sinais mínimos, a diferença de fase entre as ondas deve ser um múltiplo ímpar de :
Manipulando a equação pra fazer aparecer a frequência, como no item anterior, vamos ter:
Sendo
Quando :
Tá na faixa!
Quando
Tá na faixa!
Quando
Tá na faixa!
Pra valores maiores de surgem frequências acima de
Resposta
a)
e
b)
Exercício Resolvido #5
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 22
A Fig. 17-38 mostra quatro fontes sonoras pontuais isotrópicas uniformemente espaçadas ao longo de um eixo . As fontes emitem sons de mesmo comprimento de onda e mesma amplitude e estão em fase. Um ponto é mostrado sobre o eixo . Suponha que quando as ondas se propagam até a amplitude se mantém praticamente constante. Que múltiplo de corresponde à amplitude da onda resultante em se a distância mostrada na figura é (a) , (b) , (c) ?
Passo 1
O enunciado pede para desconsiderarmos a redução da amplitude com a distância, portanto, iremos analisar somente a interferência causada pelas 4 fontes em fase. Então vamos relembrar a relação da interferência com a diferença de caminho:
Passo 2
- Com , temos que:
- Já para , o mesmo fenômeno acontece, mas com os pares 1ª – 2ª e 3ª – 4ª. Logo:
- Com a história é diferente: a 1ª e a 2ª fonte irão emitir ondas que chegaram em fase em .
Como é inteiro, parece que ele não se encaixa em nenhum caso, né? Calma! Se liga na distância entre a 1ªe a 3ª fonte, ela vale , ou seja:
Portanto, elas vão agir destrutivamente, fazendo com que as ondas dessas duas fontes não cheguem em . Perceba que o fenômeno acontece da mesma maneira para a 2ª e 4ª fonte. Logo:
Passo 3
Passo 4
E mais! O mesmo fenômeno irá acontecer com a 2ª e 3ª fonte, bem como a 3ª e a 4ª. Ou seja, a amplitude que chega ao ponto é 4 vezes maior que a amplitude original.