Ondas Estacionárias
Produzido por Leonardo de BemTeoria
Fala aí! Seja bem vindo ao Responde Aí! Bora aprender tudo sobre Ondas Estacionárias de uma vez por todas?!
O que são ondas estacionárias?
Ondas estacionárias são ondas com um padrão de vibração que não se altera ao longo do tempo. Elas são formadas pelo encontro de duas ondas idênticas que se propagam em direções opostas.
Calma, vou explicar melhor! Você já brincou de pular corda?
Se você amarrasse a corda em algum ponto fixo na parede e começasse a movimentar ela pra cima e pra baixo, como ela iria se comportar?

No primeiro momento quando você impulsiona a corda, ela faz um movimento ondulatório na direção da parede. Após chegar na parede a onda é refletida e volta em um movimento oposto à onda inicial.
Então temos um onda indo em direção à parede e outra voltando, elas vão se chocar, certo?! É ai que temos a formação da onda estacionária!
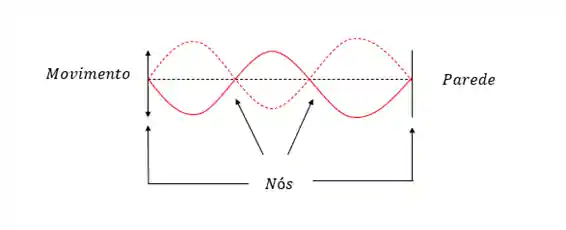
Como podemos observar na imagem acima, a onda é composta por nós, que vão ocorrer nas extremidades das cordas e também nos encontros das ondas. Nas ondas estacionárias a posição dos nós nunca munda ao longo do tempo!
Velocidade das Ondas Estacionárias
A velocidade da onda estacionária é calculada a partir da equação fundamental da onda, dada por:
é a velocidade da onda em ; é a frequência da onda em ; é o comprimento de onda, em .
Fórmulas das Ondas Estacionárias
Vamos imaginar um exemplo de duas ondas indo em direções opostas como foi mostrado e cada uma tem a seguinte equação da onda:
Ué, mas como eu sei que elas estão opostas?
Basta olhar pro sinal dentro do seno, se for negativo o sinal ela se desloca pro sentido positivo do eixo. Se for positivo o sinal ela se desloca pro sentido negativo do eixo. A dica é lembrar que o sinal indica o sentido oposto do deslocamento ok?
Somando as duas ondas teremos:
Depois de algumas manipulações, ficamos com:
Em frequências de ressonância o tempo não vai influenciar e a fórmula para ondas estacionárias será:
Frequência de Ressonância
A frequência de ressonância é uma frequência capaz de produzir uma onda estacionária. Por exemplo, para o exemplo do início do texto, de comprimento
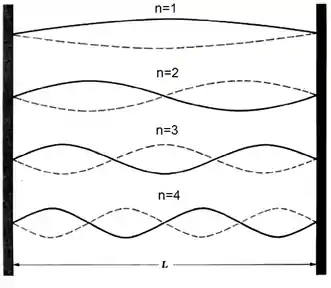
Cada desses casos são conhecidos como modos de vibração ou harmônicas. O primeiro modo é chamado de modo fundamental
Podemos calcular a frequência de ressonância, para qualquer modo de vibração, usando a seguinte fórmula:
Onde
Nós e Ventres
Como vimos lá em cima, os nós são os pontos mínimos que ocorrem nas extremidades das cordas e nos encontros das ondas.
A gente consegue calcular a posição dos nós em função de
Os ventres são os pontos máximos da onda estacionária onde a amplitude é máxima. A equação da posição dos nós em função de
Ondas Estacionárias em Tubos Sonoros
As ondas estacionárias também podem ser formadas quando o ar passa por tubos sonoros, que podem ser abertos ou fechados.
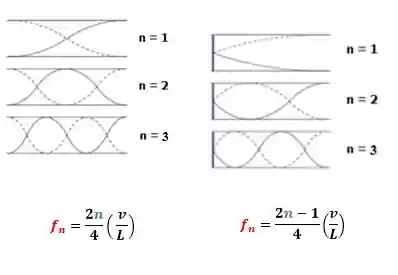
Esse fenômeno acontece em instrumentos de sopro, como a flauta doce!
Ondas Estacionárias: Vídeo Aula
Agora se liga nessa vídeo aula supercompleta sobre ondas estacionárias! 👇
Agora vamos praticar com exercícios?!
Frequência de Ressonância
Nós e Ventres
Ondas Estacionárias: Vídeo Aula
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 144-40
Uma corda com cm de comprimento tem uma massa de g e um tensão de .
- Qual é a velocidade de uma onda nesta corda?
- Qual é a frequência de ressonância mais baixa desta corda?
Passo 1
- Vamos aplicar aqui a relação entre velocidade, densidade linear e tensão:
- Sabemos que a frequência de ressonância é calculada por:
Passo 2
Como é pedida a mais frequência de ressonância mais baixa, usaremos o modo de vibração valendo .
Resposta
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 144-41
Para um fio com m de comprimento, de massa e uma tensão de , determine, para as ondas estacionárias formadas:
- A menor frequência
- A segunda menor frequência mais baixa
- A terceira menor frequência .
Passo 1
Vamos começar aplicando aqui a relação entre velocidade, densidade linear e tensão:
Passo 2
Sabemos que a frequência de ressonância é calculada por:
Vamos aplicar para cada item
- Na menor frequência, o modo será igual a 1(. Logo:
- Na segunda menor frequência, o modo será igual a 2
- Na terceira menor frequência, o modo será igual a 3
Resposta
Exercício Resolvido #3
UFF – Lista de Exercícios de Ondas - Questão 40
Quando uma massa é amarrada à extremidade de um barbante longo e fino, suspenso pelo teto, a frequência do segundo harmônico do barbante é . Acrescentando-se uma carga adicional de à massa pendurada, a frequência do segundo harmônico aumenta para . Qual é o valor de ?
Passo 1
Para determinar o valor de , precisamos relacionar as duas frequências em função da massa. Temos que a frequência é dada por:
Podemos relacionar a velocidade à tração:
Onde é a tração e é a densidade linear da corda. Juntando as duas equações, temos:
Para a primeira situação, temos:
Para a segunda situação, temos:
Dividindo as equações, temos:
Substituindo os valores, temos:
Resposta
Exercício Resolvido #4
UERJ, Física 2, Lista para P1, Lista de Ondas, Extra - 8
Uma corda de nylon de uma guitarra tem uma densidade linear de e está sob tensão . Os suportes fixos distam . A corda vibra no trem de onda estacionário visto na figura a seguir.
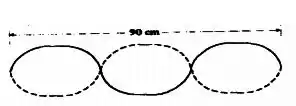
Calcule:
A velocidade
O comprimento de onda
A frequência das ondas componentes cuja superposição causa esta vibração
Passo 1
Primeiro vamos resolver a :
Encontrar a velocidade é simples nesse caso, pois temos a Tensão da corda e a sua densidade linear. A gente deve usar essa equação, então:
Sendo:
Temos:
Pronto! Vamos usar essa informação também na .
Passo 2
Como a onda é estacionária, a gente pode usar a relação:
Onde é comprimento total do fio. Isolando :
Como são 3 picos, ou 3 metades de onda, Além disso, o enunciado nos diz que . Substituindo:
Passo 3
c)
Nas letras anteriores a gente conseguiu achar o ! Agora, queremos a frequência, por isso vamos utilizar esse valor na equação:
Aplicando o valor de e :
Resposta
Resposta:
Exercício Resolvido #5
UFRJ, Física 2, Prova 2, 2013.1 – M08
Enquanto a corda de uma guitarra está vibrando, você toca levemente em um ponto que se situa na metade da corda para garantir que a corda não vibra naquele ponto. Que modos normais NÃO podem estar presentes na corda enquanto você a segura assim?
- Todos os modos vão estar presentes.
- Todos os modos com número par de nodos.
- Todos os modos com número ímpar de nodos.
- Somente o modo fundamental pois tem nodo no centro
- Somente o terceiro modo pois não tem nodo no centro.
Passo 1
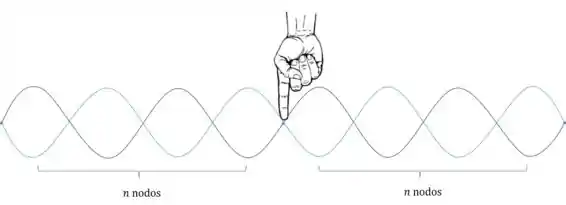
Quando temos uma corda presa por dois pontos podemos ter uma quantidade inteira positiva de nodos. Então, entre um extremo da corda e seu dedo será igual tanto pela direita como pela esquerda já que a onda deve ser simétrica, então temos
Teremos então só nodos ímpares, e não poderemos ter nodos pares.
Resposta
Letra B
Exercício Resolvido #6
USP, Física 2, Prova 2, 2013 – Questão 3
A taxa de transferência de energia por uma onda ao longo de uma corda (a potência instantânea) é dada por:
Onde é a tensão.
- Usando a expressão (1), obtenha para uma onda estacionária dada por:
- Calcule a potência média por período transportada pela onda para todo o
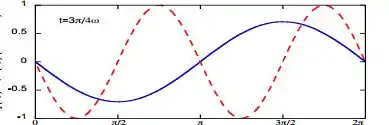
- Para uma onda estacionária dada pela expressão (2), faça gráficos de e do deslocamento em função de para: , , , e .
- Qual o valor da potência instantânea nos nós e nos ventres da onda?
Passo 1
a)
Bom, aqui a gente só precisa calcular as duas derivadas parciais da fórmula e fazer o produto entre elas. é a tensão da corda, então vamos considerá-la como um dado do problema. Assim:
Derivando a expressão em relação ao tempo:
E em relação a :
Logo:
Bom, o produto vai dar positivo. Arrumando isso:
Usando a expressão:
Vamos usar isso pra e
Passo 2
b)
O valor médio tem uma dependência temporal, certo? Então, olhando pra expressão da potência, nós podemos concluir que a potência média vai depender do termo da expressão que depende do tempo, ou seja,
E qual o valor médio disso?
Bem, é uma função senoidal, logo tem valor em um período como o valor médio. (Lembra, o seno varia de a 1, entre eles fica o ).
Logo, a potência média será:
Passo 3
c)
Pra :
E:
Logo o gráfico normalizado será:
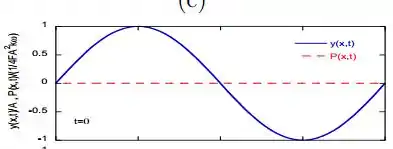
Onde a linha contínua representa e pontilhada a potência.
Para :
E a potência:
Logo:
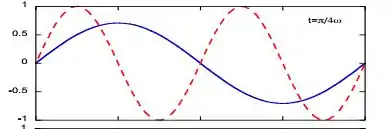
Para
E a potência:
Logo:
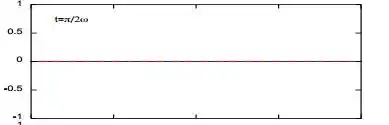
Pra
Logo:
Passo 4
d)
As ondas estacionárias possuem nós e ventres distanciados de si por uma distância .
Então podemos dizer que os pontos onde estão os nós e ventres de uma onda estacionária numa corda são:
Só que olhando a expressão da potência numa corda:
Percebemos que a potência será nula quando:
Opa! Esses são os nós e ventres. Ou seja, nos nós e ventres a potência é igual a :
Resposta
a)
b)
c)
Gráficos acima.
d)
Exercício Resolvido #7
UFRJ, Física 2, Prova 2, 2015.1 – Questão 5- Modificada
Considere uma corda feita de um material homogêneo. Qual das afirmativas a seguir está INCORRETA?
- Uma onda refletida em uma extremidade tem sempre uma frequência idêntica à onda incidente.
- A soma de uma onda totalmente refletida por uma extremidade e da onda incidente formará sempre uma onda estacionária
- Duas condições de contorno são suficientes para que o número de onda seja quantificado.
- Há propagação de energia ou de momento numa onda estacionária.
- Uma quantificação do número de onda implica numa quantificação da frequência angular.
Passo 1
Vamos analisar uma por uma:
a) Verdade. A função de onda é do tipo:
Quando ocorre uma reflexão, nós podemos até mudar o sinal que vem na frente de , que é a frequência angular e, logo, tem a ver com a frequência linear, mudar o sinal que vem na frente de , etc, mas não podemos mudar o valor de
Pensa só, porque a ponta da corda faria ela oscilar mais rápido ou mais lento se estamos considerando que não há nem dissipação nem incremento de energia?
Passo 2
b) Verdade.
Sim, essa é a definição de uma onda estacionária. É superposição da mesma onda, só que indo no sentido contrário, ou seja, refletida.
Passo 3
c) Verdade.
O que são condições de contorno? Nesse contexto, podemos entender como os valores de pra certos valores de ou
Bom, a equação de uma onda é dada por:
Se usarmos, por exemplo, um valor pra:
E outro assim:
Nós vamos ter um sistema com duas varias e duas equações:
Então, esse sistema tem solução e a gente pode determinar
Passo 4
d) Incorreta.
Não há propagação de energia e de momento nas ondas estacionárias. Por quê? Bom, a energia e o momento, numa onda comum, são transmitidos pelas partículas da corda.
Uma vai passando pra outra, por assim dizer.
No entanto, no caso de uma onda estacionaria, existem os nodos. E os nodos não se movem, certo?
Então eles meio que bloqueiam o transporte normal de energia. Assim, a energia em uma onda estacionária está presa no espaço.
Passo 5
e) Verdade.
Aqui a questão está considerando que a velocidade da onda é conhecida. Aí, se você souber o valor de , você descobre o valor de
Então, a resposta é:
d)
Resposta
d)
Exercício Resolvido #8
PUCRIO, Física 2, Prova 2, 2012.2 – Questão 1
Uma corda submetida a uma tensão de e fixa nas duas extremidades, oscila num padrão de onda estacionária correspondente ao terceiro modo normal de vibração. Uma das extremidades da corda encontra-se em e o deslocamento da corda é dado por:
(Sistema Internacional de Unidades)
Determine o comprimento da corda.
Calcule a velocidade das ondas na corda e a massa total da corda.
Obtenha a expressão da velocidade transversal das partículas da corda em função de e . Calcule essas velocidades em , nas posições .
Faça um desenho da corda em , indicando as posições dos nós e colocando os vetores velocidade nas posições e.
Desenhe a corda depois de decorrido um quarto de período .
Passo 1
Para determinar o tamanho da corda, precisamos atentar para um detalhe dado no enunciado, temos a informação de que a corda oscila em um padrão estacionário correspondente ao terceiro modo de vibração, temos então:

Ou seja, temos pontos (nós) onde a função será igual a zero, ou seja, temos que esses pontos ocorrem quando é igual a . Ou seja, deve valer e para cada um dos nós, sendo no primeiro e no último!
Então, para determinar o comprimento da corda, basta calcular quanto vale para que seja igual a !
Passo 2
Da função , podemos extrair algumas informações, se liga! Temos que o número de onda , pois essa é a constante que multiplica , pela definição de , temos:
Além disso, temos que , da definição de , temos:
Agora é só lembrar de e correr pro abraço!
Para determinar a massa, precisamos lembrar da seguinte relação:
Onde é a densidade linear da corda, vamos primeiro determinar seu valor!
Para determinar a massa, basta fazer:
Passo 3
Para determinar a velocidade transversal, vamos precisar derivar a função , que temos, se liga!
Agora é só calcular a velocidade nos pontos pedidos, simbora! Precisamos calcular essas velocidades em , nas posições .
Para , temos:
- Para , temos:
- Para , temos:
- Para , temos:
Passo 4
Para fazer o desenho da corda, precisamos relembrar de algumas coisas. Primeiro, temos que a corda oscila no terceiro modo de oscilação, ou seja, temos uma configuração com nós, sendo que são as extremidades. Além disso, para , temos que para todos os valores de ,ou seja, a corda está esticada sobre o eixo . Para expressar os vetores, basta notar o sentido da velocidade que calculamos no item anterior. Como temos que o eixo aponta para cima, teremos então o seguinte desenho:
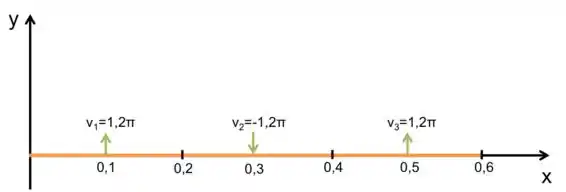
Onde os nós estão indicados por traços pretos no eixo , correspondendo aos pontos , , e , e os vetores velocidade estão destacados em verde.
Passo 5
Para poder desenhar a corda, precisamos primeiro determinar o instante de tempo indicado, temos que , podemos determinar o período pois sabemos a frequência , se liga!
Para , temos:
Substituindo em , temos:
Agora é só plotar esse gráfico, teremos algo semelhante a isso:
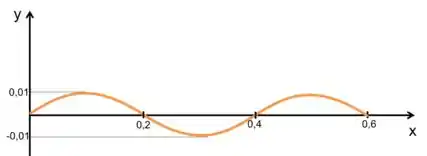
Resposta
e
Ver desenho acima.
Ver desenho acima.
Resposta
Ei, a resposta está no passo a passo :)