Tubos Sonoros
Teoria
Fala aí! Bora aprender TUDO sobre tubos sonoros com o Responde Aí?
Antes de qualquer coisa, você sabe o que são tubos sonoros?
Tubos sonoros são basicamente tubos com ar, ou algum gás onde são produzidas ondas estacionárias longitudinais em uma frequência sonora!
-Que?!!
Calma vou te dar um exemplo!! Quando você era criança você já tocou, ou pelo menos brincou com uma flauta doce?
Se sim, você sabe que basta colocar um dedo em um dos furos da flauta e o som emitido já sai diferente de antes. Mas por que o som muda só com esse ato de tapar um furo?
Hoje a gente vai entender isso!
Pra começo de conversa a flauta funciona como um tubo sonoro e existem dois tipos de tubos: os tubos sonoros abertos e os tubos sonoros fechados, bora aprender sobre eles?
Ahhh, e respondendo a pergunta inicial: Quando tapamos um furo o comprimento de onda do som dentro da flauta muda, mudando também a sua frequência e por isso ouvimos um som diferente!
Ondas Formadas em Tubos Sonoros
Antes da gente prosseguir, precisamos entender alguns conceitos importantes!
Nos tubos sonoros temos uma superposição de ondas em frequências de ressonância. Onde as ondas se encontram temos os nós e nos pontos de máximo temos as amplitudes máximas.
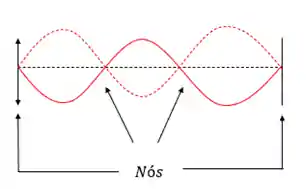
Veja mais: Ondas
Tubos Sonoros Abertos
Num tubo sonoro aberto, a onda sempre apresenta amplitudes máximas nas extremidades e a configuração das ondas em frequência de ressonância no tubo muda com o número harmônico
Saca só a imagem abaixo:
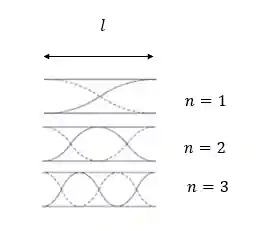
Na figura acima, o primeiro caso pode ser chamado de harmônico fundamental ou primeiro harmônico
Podemos olhar também quantos comprimentos de onda
Olhando para as figuras podemos ver que para
Logo, a cada nó novo, temos dentro do tubo mais meio comprimento de onda.
A partir disso, podemos escrever o comprimento do tubo em função do comprimento de onda e do número de nós
Então, nesse caso, podemos verificar que as frequências de ressonância são dadas pela seguinte fórmula:
Onde
Tubos Sonoros Fechados
No tubo fechado, existe uma extremidade aberta e uma fechada.
Na extremidade aberta, a onda apresenta amplitude máxima e, na fechada, a amplitude é mínima e também é um nó. Da mesma forma que no tubo aberto o número de nós representa o harmônico:
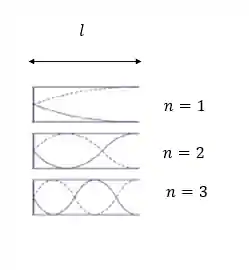
Aqui sempre vamos ter um número ímpar de quartos de comprimento de onda
Onde
Isso para
Exemplo
Pra gente aprender legal vamos calcular essas tais frequências de ressonância pro tubo abaixo.
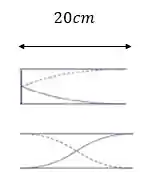
Nesse caso vamos considerar que a velocidade do som se mantém pros dois casos
Pro caso do tubo fechado temos o primeiro harmônico e podemos ver isso pelo número de nós
E no caso do tubo aberto também temos o primeiro harmônico e podemos ver isso pelo número de nós
Comparando as frequências a gente observa que pro tubo aberto a frequência de ressonância é bem maior do que pro tubo fechado, pra uma mesma velocidade e mesmo harmônico.
Ou seja, se estivermos ouvindo o som dessa onda, vamos ouvir dois sons diferentes!
Agora, vamos praticar com exercícios?!
Ondas Formadas em Tubos Sonoros
Tubos Sonoros Abertos
Tubos Sonoros Fechados
Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP-Questão 3 - P2.2012 (Noturno)
Um pequeno alto-falante é alimentado por um oscilador de áudio com uma frequência que varia de a . Um tubo cilíndrico tem de comprimento e as duas extremidades abertas, e é colocado próximo ao alto-falante. A velocidade do som no ar no interior do tubo é . Para quais frequências o som do alto-falante produz ressonância no tubo?
Passo 1
Se as duas extremidades são abertas, vamos usar a equação:
Vamos usá-la pra descobrir as frequências normais do tubo.
Para
:
E para e maiores, as frequências saem da faixa dos alto-falantes. Logo, são essas as frequências de ressonância.
Resposta
Frequências:
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 41
No tubo , a razão entre a frequência de um certo harmônico e a frequência do harmônico precedente é 1,2. No tubo , a razão entre a frequência de um certo harmônico e a frequência do harmônico precedente é . Quantas extremidades abertas existem (a) no tubo e (b) no tubo ?
Passo 1
Conhecemos as fórmulas dos tubos abertos e fechados:
- Aberto:
- Fechado:
Como queremos a frequência de harmônicos sucessivos temos, primeiro para tubos abertos (duas extremidades abertas):
Já para tubos fechados (uma extremidade aberta):
Passo 2
a)
Agora vamos analisar o 1º caso. No tubo , a razão entre as frequências sucessivas deu . Em qual das expressões que encontramos acima nós podemos variar , que é um inteiro, de forma que a razão dê ? Vamos ver:
Se o tubo for aberto:
Mas se o tubo for fechado, teremos:
Como tem que ser um inteiro, o tubo tem que ser aberto!
Passo 3
b) Já no tubo , temos que a razão entre as frequências é de . Vamos testar primeiramente para o tubo aberto em uma única extremidade:
Pronto! deu inteiro. Concluímos então que o tubo possui apenas uma extremidade aberta.
Resposta
- Duas extremidades abertas
- Uma extremidade aberta
Exercício Resolvido #3
USP-P1-2014.1-Q5
A figura mostra uma “‘flauta” simplificada, com a extremidade aberta. Há também uma grande abertura em (próxima ao bocal) e dois orifícios em e , tais que e . Sabe-se que e que a velocidade do som é Qual a frequência que se espera ouvir ao soprar a flauta com o dedo tapando ?
- Não há como excitar uma onda no tubo, já que e estão à mesma pressão externa.
- .
- .
- .
Passo 1
Bom galera, eu sei que é tentador tentar aplicar essa equação aqui nessa questão:
Mas não é por ai. Nós vamos resolver esse problema apenas lembrando das ondas de pressão que causam o som, além da geometria da flauta.
Passo 2
Bom, os pontos e estão em contato direto com a atmosfera, ou seja, representam nós de pressão. Mas a gente sabe que a onda que se forma dentro de um tubo sonoro é uma onda estacionária e que, no estado fundamental, a distância entre dois nós é dada por .
Ou seja, .
E quanto vale
O enunciado nos diz que e que . Se , então e
Logo:
Passo 3
Agora fica fácil. Já temos o comprimento de onda e a velocidade do som. Vamos achar a frequência usando:
Resposta
d)
Exercício Resolvido #4
UNICAMP-Questão 3 - P2.2010 Noturno
Um tubo , que possui de comprimento e é aberto em suas duas extremidades, vibra na sua terceira frequência harmônica mais baixa. Outro tubo , de comprimento , é fechado em uma de suas extremidades e vibra em sua segunda frequência harmônica mais baixa. As frequências dos tubos e coincidem. Dado:
- Encontre as posições do tubo em que estão os nós de deslocamento.
- Encontre o comprimento do tubo .
Passo 1
a)
Bem, aqui a gente vai precisar usar a fórmula que relaciona o do tubo com o comprimento da onda. Para um tubo aberto, essa fórmula é:
Sendo
Ótimo! Agora podemos terminar a solução simplesmente desenhando a forma da onda estacionária em um tubo aberto. Essa é a forma mais simples de se visualizar! Vamos lá:
Uma onda estacionária num tubo aberto tem a seguinte forma:
Na figura temos, em sequência, Então a forma de onda que queremos é a última, .
É fácil desenhar a forma de onda de um tubo aberto: basta a gente fazer primeiro uma “ondinha” de extensão , depois um meio comprimento completo, depois outro, e outro... quantos forem suficientes, e depois finalizar o desenho com outra “ondinha” de extensão
Beleza! A gente consegue ver claramente onde ficam os nós. Eles ficam em:
E essas são as posições dos três nós!
Passo 2
b)
Aqui a gente mata a questão simplesmente igualando as frequências, já que elas são iguais.
Mas vamos antes montar a expressão pra frequência do tubo , que é um tubo fechado:
OBSERVAÇÃO: Você também poderia encontrar a fórmula
Repare que as duas fórmulas, apesar de parecerem diferentes, são iguais. Porque em um dos casos começa em zero, e no outro em . Assim, os valores acabam sendo idênticos. Sacou?
Fim da observação.
Lembrando que queremos achar o tal do Vamos usar:
Como começa em o nosso segundo harmônico é em , logo:
E agora vamos montar a expressão pra frequência de
Logo, comparando os dois:
Resposta
a)
b)
Exercício Resolvido #5
UFRJ-P2-2014.2-Q4(III e IV)
Considere dois tubos de ar de mesmo comprimento e mesma seção transversal, um deles fechado numa das extremidades, e o outro, aberto em ambas, e ondas sonoras propagando-se nestes tubos. Considere as afirmações abaixo:
O deslocamento é máximo na extremidade do tubo aberto pois há um máximo de onda de pressão neste ponto.
O deslocamento é máximo na extremidade do tubo aberto pois há um nodo da onda de pressão neste ponto.
O comprimento de onda do modo fundamental, no tubo fechado, é o dobro do comprimento de onda deste modo no tubo aberto.
O comprimento de onda do modo fundamental, no tubo aberto, é o dobro do comprimento de onda deste modo no tubo fechado.
Qual(is) da(s) afirmação(ões) acima é(são) verdadeira(s)?
- .
- e .
- e
- e
- e
- e
- e .
Passo 1
Vamos lembrar dos padrões de deslocamento que aparecem nos tubos abertos e fechados.
Aberto:
Fechado:
Passo 2
Vamos lá:
Nas extremidades dos tubos abertos não pode haver um máximo de pressão pelo seguinte motivo: ali o ar que tá dentro do tubo, um ar com pressão oscilante, entra em contato com o ar da atmosfera, que tem uma pressão fixa. Então nas pontas dos tubos abertos existem, na verdade, nós de pressão.
Aí sim tá certo. Podemos ver isso com o padrão das ondas estacionárias nos tubos abertos e também por causa do lance da pressão fixa da atmosfera. Lembre-se de uma coisa: onde tem nó de pressão tem máximo de deslocamento e vice-versa.
Passo 3
Pra um tubo aberto, temos que:
Modo fundamental implica em . Logo:
Para um tubo fechado, temos que:
No modo fundamental, :
Ou seja, realmente o comprimento é o dobro do tubo aberto.
Passo 4
: Acabamos de ver que não é o comprimento do aberto que é o dobro do fechado, e sim o contrário.
Logo, a resposta certa é:
g)
Resposta
g)