Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Intensidade Sonora

Ver Todos os Exercícios

Teoria

Fala aí! Seja bem vindo ao Responde Aí! Bora conversar sobre Intensidade Sonora?!

O que é Intensidade Sonora?

A intensidade sonora é a qualidade que nos permite distinguir se um som produzido é forte ou fraco. Ela está ligada à quantidade de energia que é propagada pela onda sonora!

A intensidade mínima ou limiar da audibilidade é , abaixo dessa intensidade nenhum som é ouvido pelos seres humanos. E o limite superior, chamado de limiar da dor, é á, intensidades sonoras acima desse limite causam danos nos nossos ouvidos.

Fórmula da Intensidade Sonora

A intensidade sonora pode ser calculada a partir da seguinte fórmula:

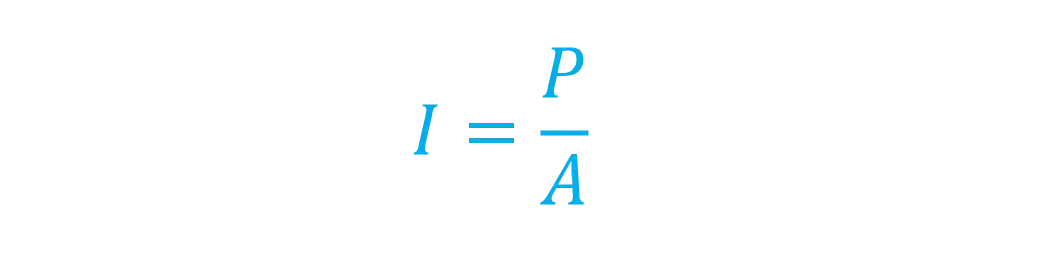
Fórmula da Intensidade Sonora
Fórmula da Intensidade Sonora

Onde é a intensidade sonora, medida em , é a potência sonora e é a área em torno da fonte até o ponto de interesse. Se considerarmos a fonte como uma fonte pontual, e como o som se propaga para todas as direções igualmente, essa área vai ser a área de uma superfície esférica:

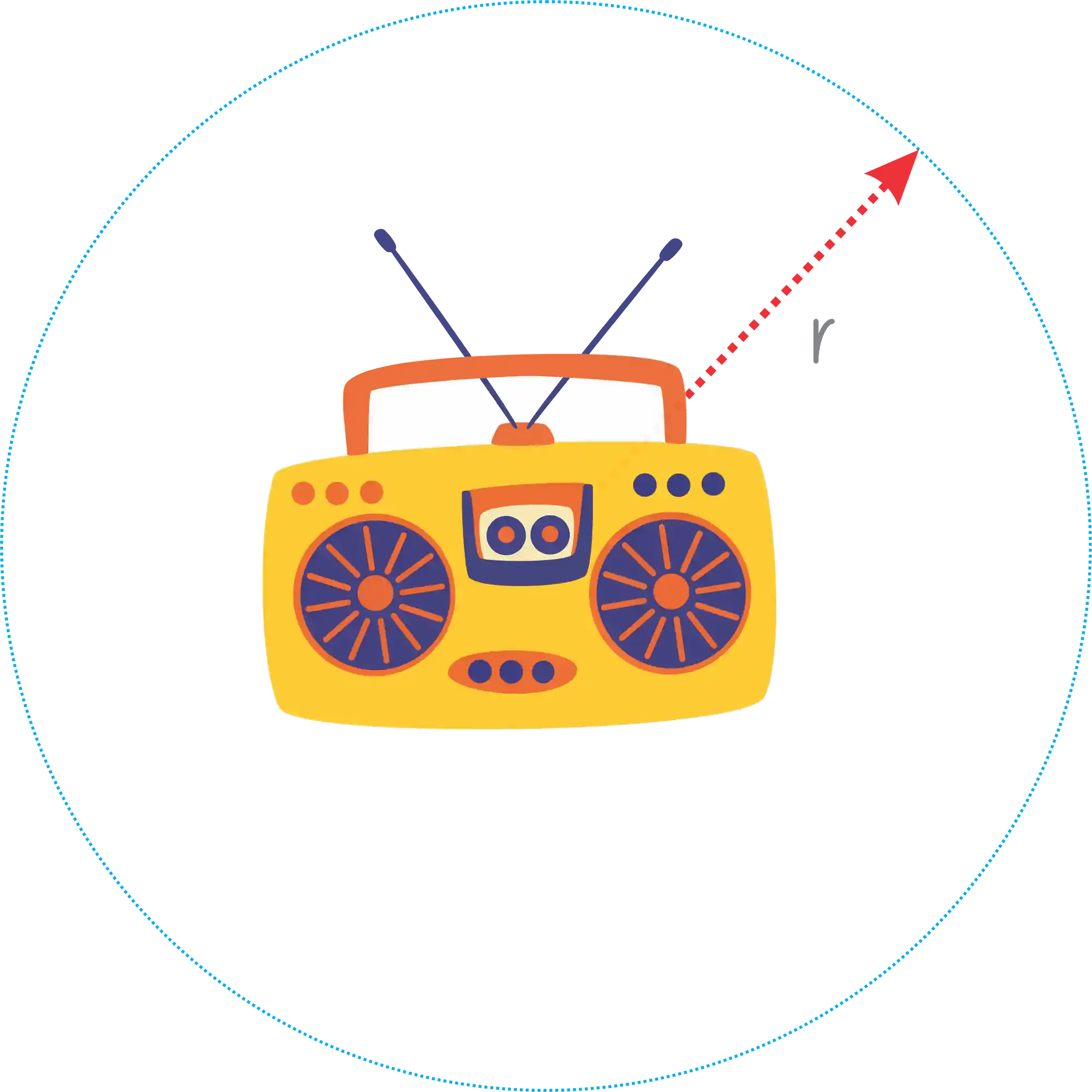
Intensidade Sonora: Fonte
Intensidade Sonora: Fonte

Nesse caso, podemos reescrever a fórmula da intensidade sonora usando a área de uma esfera:

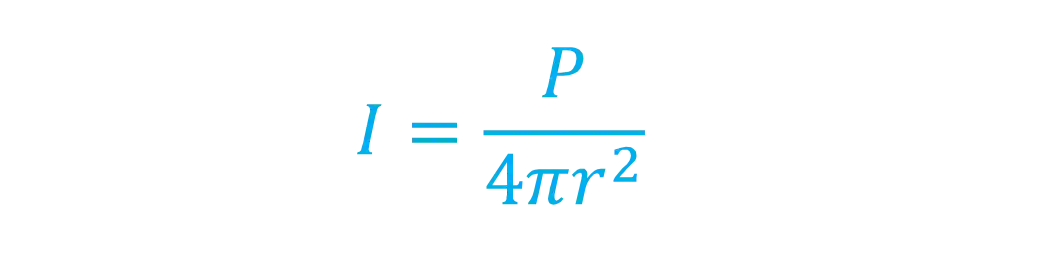
Fórmula da intensidade sonora para uma fonte pontual
Fórmula da intensidade sonora para uma fonte pontual

Beleza, mas como a intensidade sonora pode ser cobrada em exercícios?!

É o que a gente vai ver agora! Se liga nesse vídeo abaixo ou então clique aqui pra conferir nossa lista com exercícios resolvidos! 😉

Exemplo: Variação da Intensidade Sonora coma Distância

Imagina que em um certo dia você está assistindo uma videoaula irada do R.A mas precisa ir na cozinha buscar um copo d’água. Qual será a variação da intensidade sonora quando você estiver na cozinha?

Dados: , e .

Temos a fórmula da intensidade sonora>

Para calcular a variação da intensidade sonora, fazemos:

Substituindo os dados, temos:

A variação da intensidade sonora será:

Nível Sonoro

O nível sonoro é uma função logarítmica da razão entre a intensidade medida e a intensidade mínima audível e é geralmente designado por :


Quando a função logarítmica está multiplicada por 10, como está definida acima, a unidade usada é o decibel . No entanto, podemos encontrar uma definição onde a função logarítmica não está multiplicada por . Nesse caso, a unidade será o bel .

Agora vamos praticar com exercícios?


Nível Sonoro

Exercícios Resolvidos

Exercício Resolvido #1

Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 24

Uma fonte pontual de 1,0   W emite ondas sonoras isotropicamente. Supondo que a energia da onda é conservada, determine a intensidade (a) a 1,0   m e (b) a 2,5   m da fonte.

Passo 1

Já vimos que a intensidade é dada por:

I = P A

E para fontes isotrópicas a área deve ser considerada como a área de uma esfera:

A = 4 π R 2

Logo, temos:

I = 1 4 π R 2

Passo 2

  1. Aqui, R = 1,0   m :

    2. I = 1 4 π → I = 0,08 W m 2

    Passo 3

  2. Já aqui, R = 2,5   m :

I = 1 4 π   .   2,5 2 → I = 0,013 W m 2

Resposta

  1. 0,08 W m 2
  2. 0,013 W m 2

Exercício Resolvido #2

Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 26

A diferença entre os níveis sonoros de dois sons é 1,00   d B . Qual é a razão entre a intensidade maior e a intensidade menor?

Passo 1

A expressão para nível sonoro (em dB) é:

n = 10 log ⁡ I I 0

Foi dado no enunciado que:

n 1 - n 2 = 1   d B

Como o nível cresce junto com a intensidade, se n 1 > n 2 , I 1 > I 2 , e então:

1 = 10 log ⁡ I 1 I 0 - 10 log ⁡ I 2 I 0

Usando propriedade da subtração de logaritmos:

1 = 10 log ⁡ I 1 I 0 I 2 I 0 → 0,1 = log ⁡ I 1 I 2

E então:

I 1 I 2 = 10 0,1 = 1,26

Resposta

I 1 I 2 = 1,26

Exercício Resolvido #3

PUCRIO-P2-2012.1-3i a

Na figura abaixo, duas fontes sonoras F 1 e F 2 , separadas por uma distância D = 3,0   m , estão em fase e emitem ondas isotropicamente com potências P 1 = 2,5 .   π   W e P 2 = 1,6 .   π   W , respectivamente. Um ouvinte O se encontra a uma distância L = 4,0   m da fonte F 2 , como mostra a figura. Considere a velocidade do som no ar igual a 340   m / s .

a ) Calcule as intensidade e os níveis sonoros detectados pelo ouvinte O , devidos a cada uma das fontes F 1 e F 2 , separadamente.

Passo 1

a )

Para determinar a intensidade, precisamos lembrar da seguinte fórmula:

I = P s 4 . π . d 2

Onde d é a distância entre a fonte e o ouvinte.

Para a fonte 1 , temos:

I 1 = P 1 4 . π . L 2 + D 2 2

I 1 = 2,5 . π 4 . π . 4,0 2 + 3,0 2 2

I 1 = 0,025   W / m 2

Para a fonte 2 , temos:

I 2 = P 2 4 . π . L 2

I 2 = 1,6 .   π 4 . π . 4,0 2

I 2 = 0,025   W / m 2

Passo 2

Para calcular o nível sonoro, devemos lembrar da sua fórmula:

β = 10 . log ⁡ I I 0

Lembrando que I 0 = 10 - 12   W / m 2 .

Como a intensidade é a mesma para ambas as fontes, temos que:

β 1 = β 2 = 10 . log ⁡ 0,025 10 - 12  

β 1 = β 2 = 10 . ( 10,4 )

β 1 = β 2 = 104   d B

Resposta

a ) I 1 = 0,025   W / m 2 ; I 2 = 0,025   W / m 2 ; β 1 = β 2 = 104   d B

Exercício Resolvido #4

Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 17, Problema 29

O nível sonoro de uma certa fonte sonora é aumentado em 30,0   d B . Por que fator é multiplicada (a) a intensidade do som e (b) a amplitude da pressão do ar?

Passo 1

Sabemos que a expressão do nível sonoro (em dB) é dada por:

n = 10 log ⁡ I I 0

a) Se isolarmos a intensidade, temos:

I = I 0 10 n 10

Se aumentarmos o nível em 30   d B :

I ' = I 0 10 n + 30 10 → I ' = I 0 10 n 10 10 3

Chega-se então a:

I ' = 10 3 I

Passo 2

  1. Sabemos que outra relação da intensidade sonora é dada por:

I = 1 2 . ρ . v . ω 2 . A 2

No aumento do nível sonoro não alteramos ρ ,   v ,   ω , portanto I é proporcional ao quadrado de A . E o que isso significa pra gente?

Bom, já sabemos por quanto a intensidade é multiplicada no aumento do nível sonoro.

I ' = 1 2 ρ . v . ω 2 . A ' 2 = 10 3 . 1 2 ρ . v . ω 2 . A 2

Para saber de quanto foi multiplicada a amplitude, basta tirar a raiz quadrada!

A ' = 10 3   A = 31,62   A

Resposta

  1. 10 3
  2. 31,62

Exercício Resolvido #5

UNICAMP-P2-2007.2-NOT-Q3

Durante uma aula, um professor emite um som com uma potência sonora de 1,2 x 10 - 9 W . Dado que o limiar de audibilidade corresponde a I 0 = 10 - 12 W / m 2 e admitindo que o som se distribua uniformemente em todas as direções:

  1. Calcule o nível sonoro β (em d B ) que um aluno situado a 1,0 m de distância do professor detecta.
  2. Qual a distância entre o professor e o aluno, a partir da qual, se o aluno se afastar, ele certamente não ouvirá a voz do professor.
  3. Explique o que aconteceria com o valor encontrado no item a) se a frequência da voz do professor duplicasse, mantendo-se a mesma amplitude na posição do aluno. Seja β ' esse novo nível sonoro. Calcule a diferença β ' - β entre os níveis sonoros.

Passo 1

a)

O nível sonoro pode ser calculado pela fórmula:

β = 10 log ⁡ I I 0

Mas primeiro a gente tem que calcular a intensidade do som I . A intensidade do som é dada por:

I = P A = P 4 R 2 π

Onde R é a distância da fonte até o observador.

Então, pra 1 m de distância:

I = 1,2 x 10 - 9 4 π . 1 2 ≅ 10 - 10 W / m 2

O nível sonoro é:

β = 10 log ⁡ 10 - 10 10 - 12 = 20 d B

Passo 2

b)

Quando uma questão de nível sonoro te pede uma distância tal que o som não possa mais ser sentido, ela está querendo dizer que você tem que achar a distância que gera um nível sonoro igual a zero. De forma que:

β = 0   → log ⁡ I I 0 = 0 → I I 0 = 1   → I = I 0

Ou seja, esse ponto vai gerar uma intensidade igual a I 0 .

A gente sabe o valor de I 0 , então:

I 0 = 1,2 x 10 - 9 4 π R 2 = 10 - 12 → R = 1,2 x 10 - 9 4 π I 0 = 10 m

Passo 3

c)

Como I é dada por:

I = 1 2 . ρ . v . ω 2 . A 2

Se duplicarmos a frequência, quadruplicaremos a intensidade:

I ' = 4 I

E o novo nível sonoro será:

β ' = 10 log ⁡ 4 I I 0 = 10 log ⁡ 4 + 10 log ⁡ I I 0

Como β = 10 log ⁡ I I 0 , então:

β ' = 10 log ⁡ 4 + β

Então:

β ' - β = 10 log ⁡ 4

Se considerarmos log ⁡ 4 ≅ 0,6 :

β ' - β = 6   d B

Resposta

a)

β = 20 d B

b)

R = 10 m

c)

β ' - β = 6   d B

Exercícios de Livros Relacionados

Uma fonte produz uma onda senoidal de frequência angular 3000 r a d / s e amplitude 12 n m em um tubo de ar. O raio interno do tubo é 2 c m . ( a ) Qual é a taxa média com a qual a energia (soma das e
Uma onda sonora com uma frequência 300H z tem uma intensidade de 1,00μ W / m 2 . Qual é a amplitude das oscilações do ar causadas pela onda?
Em um certo ponto, duas ondas produzem variações de pressão dadas por Δ p 1 = Δ p m s e n ( ω t ) e Δ p 2 = Δ p m s e n ( ω t - ϕ ) . Nesse ponto, qual é a razão Δ p r / Δ p m , onde Δ p r é a amplitu
Uma fonte pontual emite 30,0W de som isotropicamente. Um pequeno microfone intercepta o som em uma área de0,750c m 2 , a 200m de distância da fonte. Calcule (a) a intensidade sonora nessa posição e (b
Qual é a razão entre o nível de intensidade de uma conversação normal e o nível de intensidade sonora de um murmúrio (a uma distância de 5,0 m )? (a) 10 3 (b) 2 (c) 10 - 3 (d) 1 2