Difração em Fenda Simples
Produzido por Bruno SoaresTeoria
O que é difração?
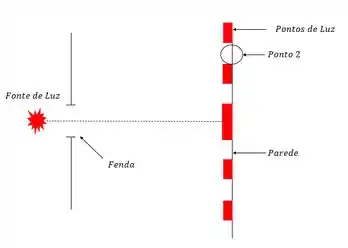
Se apontarmos um laser para uma fenda única qualquer, ele vai formar uma imagem como a que tá aí embaixo.
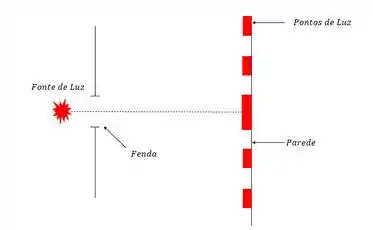
Os pontos de luz são conhecidos como franjas claras ou máximos e onde não tem luz chamamos de franjas escuras ou mínimos.
Pera aí, você tá me dizendo que uma única fonte de luz pode formar vários pontos de luz ao passar por uma fenda?
É isso mesmo e eu quero saber o seguinte, como explicar isso, pensando na propagação puramente retilínea da luz (ótica geométrica)?
Bem... não explica. Esse fenômeno é chamado difração. Ele ocorre quando a luz atinge um obstáculo que possui uma abertura (ou extremidade), e é um fenômeno puramente ondulatório.
Nesse caso, a luz se espalha e age como se fizesse uma curva (princípio de Huygens).
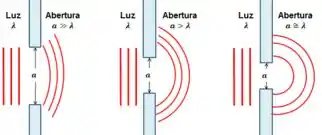
O quanto a luz se espalha depende da relação entre seu comprimento de onda e a largura da abertura. Além disso, quanto mais as ondas trafegam após atingir o obstáculo mais elas se espalham até chegar na parede.
Quando a parede está muito próxima, temos a chamada Difração de Fresnel, onde o resultado acaba se parecendo com o objeto iluminado (muda pouco em comparação com luz retilínea).
Se a parede estiver bem longe, temos a chamada Difração de Fraunhofer que foi mostrada na figura inicial, onde alguns pontos estavam iluminados e outros não.
Posição Angular das Franjas
Vamos aprender difração por uma fenda (Fraunhofer), observando os tipos de problema que podem aparecer.
O primeiro caso é encontrar o ângulo de algum ponto onde a luz não aparece. Então como encontrar o ângulo pra esse ponto 1 da figura? Sabendo que a fenda mede de largura e o comprimento da onda da luz vermelha é .
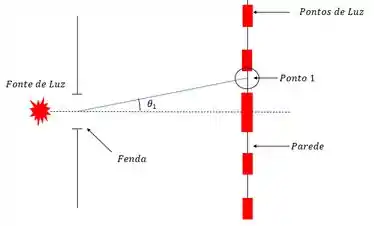
Imagine, primeiro, dois raios, conforme a figura abaixo.
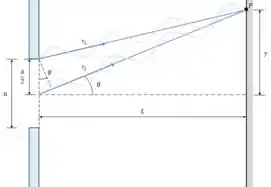
A diferença entre os dois caminhos dos raios até o ponto , responsável pela diferença de fase, é dada por:
Se essa defasagem entre os dois raios for de meio comprimento de onda, ocorre o cancelamento das ondas (interferência destrutiva).
Rearrumando temos o seguinte:
E substituindo os valores temos:
Tá beleza, mas e se me pedissem outros pontos mínimos onde a luz não aparece, tipo esse aqui?
No geral a gente vai usar a mesma equação usada no primeiro ponto só que os mínimos são múltiplos e seguem um padrão, por isso, podemos reescrever então a equação da seguinte forma.
(franjas escuras na difração, fenda simples)
Mas... de onde surgiu o ?!
O é o número do mínimo de interferência a partir do referencial que é o centro. No primeiro ponto a gente calculou o ângulo para , ou seja, o primeiro mínimo a partir do centro.
A figura agora pede a partir do centro, sendo assim:
Beleza, então se te pedirem pra calcular um ângulo de algum ponto mínimo você tá craque. E se te pedirem a posição de um ponto máximo?
Aqui basta você adicionar ao seu o valor de e a equação pra um máximo vai ficar:
E se a gente quiser a distância ao invés do ângulo?
Posição das Franjas
Ok, sabemos exatamente o ângulo de cada franja escura em relação ao centro da figura de difração. Assim, se colocarmos uma régua na figura, podemos medir... a distância. Ela não é o ângulo.
Como medir a distância do ponto 2? A qual encontramos o ângulo por último se a parede está afastada de 2 metros da nossa fenda?
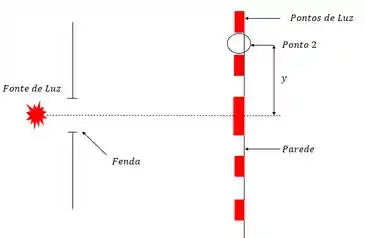
Começaremos pelas condições de mínimo:
Vamos analisar a imagem e encontrar a posição das franjas escuras usando trigonometria.
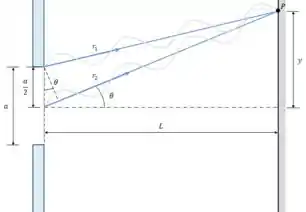
para pequenos ângulos:
E com a equação do mínimo temos:
Rearrumando teremos para cada
Que é a distância da franja escura até a franja brilhante central.
E se quiséssemos a distância de uma franja clara era só usarmos a regra usada pra posição angular de somar ao
Então vamos calcular a distância da segunda franja escura, ou seja, pra
E a franja clara de
Se a gente quisesse a distância entre franjas, nós subtraímos , de forma que:
Tipo a distância entre e .
Que? Franja negativa? Sim abaixo do centro da figura as franjas são negativas segundo o referencial!
Se liga no sinal hein!
Para franjas escuras próximas, tipo e a equação ficaria:
O quão brilhante são as luzes que vejo lá ao longe?
Cada luz que a gente vê brilha por causa da sua intensidade, a luz central é maior e mais extensa e quanto mais a gente se afasta do centro menor é esse brilho, olha como vai ficar o gráfico de intensidade das luzes conforme o ângulo aumenta.
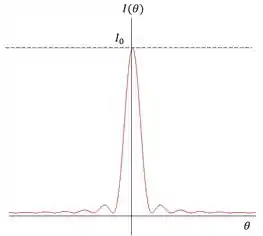
Pra intensidade da luz vale mais a pena a gente concentrar os nossos esforços em lembrar da fórmula do que deduzi-la.
Assim como quando estudamos interferência, podemos calcular a diferença de fase através da seguinte equação:
Vamos calcular a intensidade do nosso mínimo pra ver quão diferente é essa intensidade do máximo central, para o mínimo
Lembrando que pra , .
Então temos:
Ou seja, quase zero, então a gente conferiu pela intensidade que esse ponto é realmente um mínimo.
Posição Angular das Franjas
Posição das Franjas
O quão brilhante são as luzes que vejo lá ao longe?
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 137-4.
Qual deve ser a razão entre a largura da fenda e o comprimento de onda para que o primeiro mínimo de difração de uma fenda isolada seja observado para ?
Passo 1
Sabemos que os mínimos de difração são dados por:
Queremos encontrar a razão tal que o primeiro mínimo de difração seja observado para .
Passo 2
Olhando os valores possíveis de , vemos que o primeiro mínimo de difração corresponde a . Por enquanto, vamos usar .
Além disso, o seno corresponde ao nosso ângulo é .
Substituindo, temos:
Assim, a razão entre a largura da fenda e o comprimento de onda será
Passo 3
O valor corresponderia aos mínimos de difração abaixo do máximo central, ou seja, a um ângulo .
Resposta
A razão entre a largura da fenda e o comprimento de onda é .
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 143-82.
Um experimento de difração de fenda única utiliza uma luz com um comprimento de onda de , que incide perpendicularmente em uma fenda com de largura. A tela de observação está a de distância da fenda.
Qual é a distância na tela entre o centro da figura de difração e o segundo mínimo de difração?
Passo 1
A distância entre o centro da figura de difração e o mínimo de ordem quando os ângulos são bem pequenos é dada aproximadamente por:
Onde é o comprimento de onda da luz, é a abertura da fenda e é a distância entre a fenda e a tela de observação.
Passo 2
Para o segundo mínimo de difração:
E o enunciado nos diz que:
Substituindo:
Passo 3
Vamos agora tentar resolver sem a aproximação para ângulos pequenos, só para podermos comparar as respostas.
A distância angular entre o segundo mínimo de difração e o centro da figura é dada por:
Passo 4
Para achar a distância linear, usamos a tangente do ângulo:
Rearrumando:
O erro relativo de termos usado a aproximação de pequenos ângulos é de:
Ou seja, nós erraríamos por apenas . Vamos usar o valor exato na resposta final, mas lembrando que poderíamos usar o valor com a aproximação sem medo (ahn vai, é baixo, a gente pode ignorar).
Resposta
A distância do segundo mínimo de difração até o centro da tela é de .
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 137-2.
Um feixe de luz com um comprimento de onda de 441 nm incide em uma fenda estreita.
Em uma tela situada a 2,00m de distância a separação entre o segundo mínimo de difração e o máximo central é .
- Calcule o ângulo de difração do segundo mínimo.
- Determine a largura da fenda.
Passo 1
a)
Tendo a distância do segundo mínimo ao máximo central da figura de difração podemos achar o ângulo pela tangente do mesmo.
O enunciado nos diz essa distância e a distância da fenda até o anteparo .
Para transformar de radianos para graus nós usamos uma regra de 3, considerando que corresponde a :
Passo 2
b)
Já tendo o ângulo entre o centro da figura e o segundo mínimo, podemos usar a condição de interferência destrutiva para fenda de largura .
Lembrando que sendo o segundo mínimo temos e que o enunciado nos diz que a luz tem um comprimento de onda de , substituindo e rearranjando:
Resposta
a)
b)
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 137-1.
Uma fenda é iluminada com um feixe de luz que contém os comprimentos de onda e , escolhidos de tal forma que o primeiro mínimo de difração da componente coincide com o segundo mínimo da componente .
- Se , qual é o valor de ?
- Determine para que número de ordem um mínimo da componente coincide com o mínimo da componente cujo número de ordem é
- Determine para que número de ordem um mínimo da componente coincide com o mínimo da componente cujo número de ordem é
Passo 1
a)
Primeiramente, sabemos que a condição para termos um mínimo de difração é:
Além disso, o problema nos diz que o primeiro mínimo () de difração da componente coincide com o segundo mínimo () da componente , ou seja, têm o mesmo ângulo em relação ao máximo central. Assim:
Isso implica que
Como , então .
Passo 2
b)
Para achar mínimos das duas componentes que coincidem, repetimos o desenvolvimento acima, porém com diferentes ordens.
Neste primeiro caso, queremos saber qual mínimo de coincide ao mínimo de de ordem 2.
Como (visto na letra a), temos:
Passo 3
c)
Agora, queremos achar o mínimo de correspondente ao terceiro mínimo de .
Vou acelerar um pouco o procedimento, mas se igualarmos o mínimo de ordem de com o mínimo de ordem de , teremos:
Pelo fato de ser o dobro de .
Assim, teremos neste caso:
Resposta
a)
O comprimento de onda é de
b)
O número de ordem do mínimo correspondente é
c)
O número de ordem do mínimo correspondente é
Exercício Resolvido #5
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 135-36.9.
Um som de frequência sai de uma sala por uma passagem de de largura.
Em que ângulos relativamente à perpendicular à linha central da passagem alguém fora da sala não escutará nenhum som?
Considere a velocidade do som no ar de e suponha que a fonte e o ouvinte estão ambos suficientemente longe da passagem para que a difração de Fraunhofer se aplique.
Despreze os efeitos de reflexões.
Passo 1
O problema nos dá a frequência , a largura da passagem por onde o som passa, e a velocidade do som e nos pede para encontrar os ângulos de mínimos de difração.
Passo 2
Na difração, os ângulos para os mínimos de interferência podem ser encontrados a partir da equação:
Para encontrar o valor do comprimento de onda , usaremos a frequência fornecida pelo problema.
Passo 3
O comprimento de onda e a frequência estão relacionados por:
Onde:
;
;
Logo:
Passo 4
Onde:
;
;
Logo:
;
;
;
Resposta
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 137-8.
Os fabricantes de fios (e outros objetos de pequenas dimensões) às vezes usam um laser para monitorar continuamente a espessura do produto. O fio intercepta a luz do laser, produzindo uma figura de difração parecida com a de uma fenda com a mesma largura que o diâmetro do fio (Fig.36-39).
Suponha que o fio é iluminado com um laser de hélio-neônio, com um comprimento de onda de , e que a figura de difração aparece em uma tela situada a uma distância do fio. Se o diâmetro do fio é , qual é a distância observada entre dois mínimos de décima ordem (um de cada lado do máximo central) ?
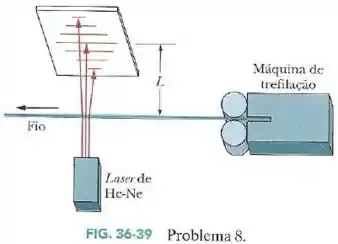
Passo 1
Neste exercício, nós queremos saber a distância entre dois mínimos de décima ordem, um de cada lado do máximo central.
Quanto maior a ordem de um dado mínimo, maior a distância angular dele até o centro da figura. Por isso, já que estamos trabalhando com o mínimo de décima ordem, é mais seguro nós não considerarmos válida a aproximação de pequenos ângulos e tentarmos resolver o exercício da forma mais exata possível.
Passo 2
Primeiramente nós encontramos a distância angular dos mínimos até o centro da figura. Isso pode ser feito pelas condições de interferência totalmente destrutiva:
O comprimento de onda da luz é de , o tamanho da “fenda” (diâmetro do fio) é e os mínimos são de ordem .
Neste caso, mesmo trabalhando com um mínimo de ordem alta, nós vemos que poderíamos ter usado a aproximação de pequenos ângulos desde o início.
Passo 3
Tendo confirmado que podemos usar a aproximação de pequenos ângulos, daqui podemos seguir o caminho que quisermos:
- Usar os dois ângulos calculados para encontrar a distância entre eles a partir da tangente ;
- Usar direto a fórmula aproximada para a distância entre dois mínimos .
Por comodidade, usarei a segunda que já nos dá direto o valor procurado, sendo a distância do fio até o anteparo de .
Apenas por desencargo de consciência, vamos calcular da forma mais exata e comprovar que ambos os caminhos dariam aproximadamente o mesmo resultado.
Substituindo os ângulos:
Ou seja, neste caso, ambos os caminhos são igualmente válidos.
Resposta
A distância observada entre os dois mínimos de décima ordem é .
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 138-11, modificado.
Uma luz monocromática com um comprimento de onda de incide em uma fenda com de largura. A distância entre a fenda e a tela é .
Considere um ponto da tela situado a de distância do máximo central. Calcule:
- O valor de nesse ponto.
- O valor de .
- A razão entre a intensidade nesse ponto e a intensidade do máximo central.
Passo 1
a)
O ângulo entre a reta que vai da fenda até o máximo central da figura de difração e a reta que vai até o ponto que queremos avaliar é .
Se olharmos essas duas retas e a distância desse ponto até o máximo central, nós temos um triângulo retângulo onde os catetos são a distância até o anteparo e a distância do ponto ao máximo central .
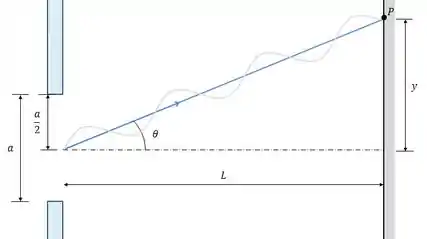
A tangente de será então:
Passo 2
b)
é a diferença de fase entre todos os raios que atingem o ponto que estamos analisando. Ela vai ser dada por:
A fenda tem uma largura de e a luz que incidente tem comprimento de onda . Substituindo esses valores junto com o ângulo encontrado no item anterior, ficamos com:
Passo 3
c)
A intensidade nesse ponto é dada por:
A razão entre essa intensidade e o máximo central vai ser
Resposta
a)
b)
c)
Exercício Resolvido #8
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 135-36.13.
Um feixe de luz vermelha de comprimento de onda igual a proveniente de um laser de hélio-neônio passa por uma fenda com largura de .
A figura de difração é observada sobre uma tela situada a uma distância de da fenda.
Defina a largura de uma franja brilhante como a distância entre os dois mínimos existentes de cada lado da respectiva franja.
- Qual é a largura da franja brilhante central?
- Qual é a largura da primeira franja brilhante situada de cada lado da franja central?
Passo 1
O problema nos dá o comprimento de onda , a distância e a largura da fenda .
a)
O problema nos diz que a largura de uma franja brilhante como a distância entre os dois mínimos existentes de cada lado da respectiva franja. No caso, para .
Assim:
Onde:
Logo:
Passo 2
Onde:
;
;
;
Logo:
Passo 3
b)
As larguras das primeiras franjas brilhantes situadas de cada lado da franja central são iguais.
O problema nos diz que a largura de uma franja brilhante como a distância entre os dois mínimos existentes de cada lado da respectiva franja. No caso, para .
Assim:
Onde:
Logo:
Passo 4
Onde:
;
;
;
Logo:
Resposta
a)
b)
Exercício Resolvido #9
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 137-7.
A distância entre o primeiro e o quinto mínimo da figura de difração de uma fenda é com a tela a de distância da fenda quando é usada uma luz com um comprimento de onda de .
- Determine a largura da fenda.
- Calcule o ângulo do primeiro mínimo de difração.
Passo 1
Neste exercício, vamos considerar desde o início a aproximação de pequenos ângulos.
Como ele só nos dá a distância entre dois mínimos, e não de um mínimo a outro, seria um tanto complicado encontrar as respostas sem essa aproximação.
A tela estando muito próxima da fenda, esperamos que essa vá ser uma boa aproximação.
Passo 2
a)
A distância entre dois mínimos, dentro da aproximação de pequenos ângulos, é dada por:
Temos a distância da fenda à tela , a distância entre o quinto mínimo e o primeiro mínimo e o comprimento de onda da luz . Rearranjando a nossa equação:
Passo 3
b)
Tendo a largura da fenda, podemos encontrar a distância angular usando a condição de interferência destrutiva.
Sendo que a aproximação de pequenos ângulos diz que
Logo:
Resposta
a)
b)
Exercício Resolvido #10
Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, pp 135-36.15
Uma fenda com largura igual a é iluminada por um feixe de raios paralelos de comprimento de onda igual a .
A figura de difração é observada sobre uma tela situada a uma distância de da fenda.
A intensidade no centro do máximo central é igual a .
- Qual é a distância sobre a tela entre o centro do máximo central e o primeiro mínimo?
- Qual é a intensidade em um ponto situado no centro do segmento que une o máximo central com o primeiro mínimo?
Passo 1
O problema nos dá a largura da fenda , o comprimento de onda , a distância entre a fenda e a tela e a intensidade para .
a)
O problema nos pede para calcular a distância sobre a tela entre o centro do máximo central e o primeiro mínimo .
Essa distância é dada por:
Onde:
;
;
;
;
Logo:
Passo 2
b)
O problema nos pede para calcular a intensidade em um ponto situado no centro do segmento que une o máximo central com o primeiro mínimo.
Esse ponto se trata da metade da distância entre o máximo central e o primeiro mínimo, logo:
A intensidade é dada por:
Onde:
Como já possuímos os valores de e, nos falta apenas descobrir o valor de para resolver o problema.
Passo 3
Analisando a figura abaixo, vemos que podemos encontrar o valor de através da seguinte relação:
Onde:
;
;
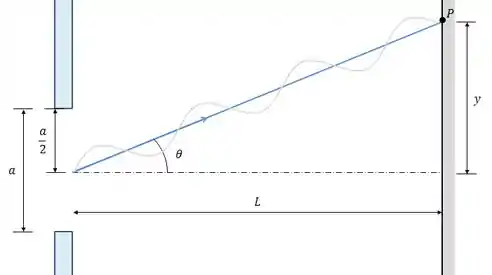
Logo:
Como então:
Passo 4
Onde:
;
;
;
Logo:
Passo 5
Onde:
;
;
;
Logo:
Resposta
a)
b)
Exercício Resolvido #11
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 138-14.
A Fig.36-41 mostra a variação do parâmetro da Eq.36-6 com o seno do ângulo em um experimento de difração de fenda única usando uma luz com um comprimento de onda de .
A escala do eixo vertical é definida por . Determine:
- A largura da fenda.
- O número total de mínimos de difração (dos dois lados do máximo central).
- O menor ângulo para o qual existe um mínimo.
- O maior ângulo para o qual existe um mínimo.
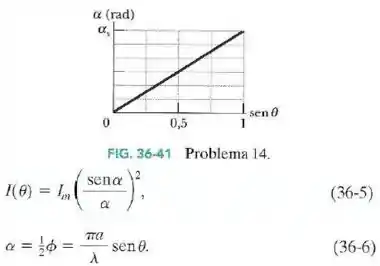
Passo 1
a)
Sabemos que
Para , temos . Além disso, o comprimento de onda da luz é de .
Rearranjando a equação:
Passo 2
b)
A condição do mínimo de difração é:
O mínimo de difração com maior ângulo possível tem que ter um ângulo menor que . Para acharmos esse mínimo, vemos qual seria o valor de para este ângulo.
O último mínimo a aparecer no anteparo será o de ordem . Assim, temos mínimos até chegar nesse.
Porém, temos que contar também os mínimos que aparecem abaixo do máximo central (ângulos negativos), que serão mais mínimos, pois a figura é simétrica.
Temos no total 6 mínimos de difração.
Passo 3
c)
O menor ângulo para o qual temos um mínimo é aquele correspondente ao primeiro mínimo .
Passo 4
d)
O maior ângulo para o qual existe um mínimo é aquele corresponde ao último mínimo do anteparo, que é o mínimo de ordem .
Resposta
a)
b)
No total teremos mínimos de difração.
c)
d)