Cinética dos Gases
Teoria
O que é isso?
Vimos que gases ideais podem ser caracterizados pelas suas propriedades macroscópicas (como pressão e temperatura), que são aquelas que nós podemos medir, sentir, visualizar. Na prática, são uma média do comportamento de zilhões de partículas.
Okay, mas por que a gente não usa uma partícula ao invés de zilhões? Parece loucura né? Tem como saber as propriedades microscópicas?
Dá pra saber a velocidade de uma única partícula? Quantas vezes por segundo uma molécula se choca com outra?
A resposta é: dá! Mas a gente vai ter que usar valores médios! =P
Chamamos isso de Teoria Cinética dos Gases.
Velocidade Quadrática Média
Imagina num cilindro de gás, várias moléculas agitadas indo de um lado pro outro cada uma com sua velocidade.
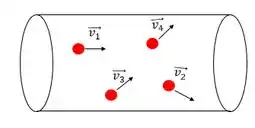
A velocidade quadrática média é a média das velocidades das partículas no sistema, no nosso desenho seria bem fácil de encontra-la já que temos só 4 partículas mas nos problemas reais são milhares de partículas super agitadas, então a gente vai achar um outro jeito de calcular essa velocidade.
A energia total de cada uma dessas moléculas é dada pelo teorema da equipartição de energia (que vamos estudar com mais detalhes depois), que diz que pra uma molécula monoatômica isso vale:
Detalhe que pra gases não monoatômicos o cálculo da energia muda, de forma geral é:
Onde pra cada situação é dado o valor da constante , porém 99% das vezes o gás é monoatômico, mas fica a dica pra quando não for.
Onde k é a constante de Boltzmann, ;
T é a temperatura do gás em Kelvin.
Como temos um gás ideal, a energia potencial é zero. Para uma única molécula de massa , temos pela conservação da energia que:
Então substituindo a energia do gás monoatômico temos:
E isolamos a nossa velocidade quadrática média.
Chamamos de velocidade quadrática média ( ou do inglês root mean square), pois vem da energia cinética, que tem a velocidade ao quadrado!
A gente ainda pode, reescrever a em função de outras paradas vamos começar usando a relação.
R é a constante dos gases ideais e o número de Avogadro. Podemos chegar em uma fórmula equivalente:
E aqui se liga:
Onde M é a massa molar do gás (quantidade de massa por número de mols), daí:
Temos ainda um terceiro jeito de se encontrar essa velocidade, vamos começar lembrando que:
Passando para o outro lado e lembrando que a densidade é dada por temos:
Daí isolamos
Substituindo na equação da velocidade quadrática média a gente tem:
Cortando e subindo , temos:
Analisando as fórmulas, vemos que quanto maior a temperatura ou maior a pressão, maior vai ser a velocidade das moléculas, como esperado.
Bora fazer um exemplo pra gente treinar, vamos encontrar a velocidade quadrática média do nitrogênio a 50, dados e
Aqui a meta é analisar qual das equações usar pra sair o mais rápido possível, temos a massa molar a constante dos gases, e a temperatura qual das equações usar? Essa aqui:
Lembrando que não é errado sair por outras mas, pra você não dar voltas é bom escolher as quais você já tem os dados, lembrando que aqui temos que converter a temperatura pra kelvin.
Daí substituindo a gente tem:
Não precisa ficar tão fissurado com as unidades, se trabalhar com Joule e Kelvin a velocidade vai sair em , como no SI.
Livre Caminho Médio
Imagine uma garrafa de com várias bolinhas de gude. Você começa a balançar essa garrafa. As bolinhas irão colidir com a parede da garrafa e entre elas, certo? Se a gente pensar numa escala microscópica é parecido com o que rola com as moléculas de gás.
O livre caminho médio é a media das distâncias que uma molécula consegue andar antes de bater, bora olhar na figura e imaginar o percurso dessa molécula aqui.
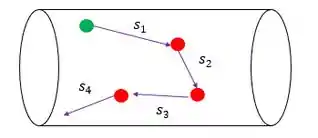
Qual seria o livre caminho médio, analisando a molécula verde? Pensando de forma simples a gente pode dizer que:
Porém quando falamos de gases, a quantidade de moléculas não é tão pequena e não faria sentido calcular assim o percurso de milhões de moléculas portanto temos uma outra forma interessante de calcular isso mais rápido.
Como Calcular?
Vamos calcular o livre caminho médio, chamado de , pela fórmula:
Onde é o volume do recipiente onde o gás está confinado, é o número de átomos ou moléculas e é o diâmetro do átomo ou molécula que compõe o gás.
Em exercicíos desse assunto, é muito comum ser pedido o diâmetro do átomo ou molécula, dado a quantidade de partículas por centímetro cúbico. Para trabalhar com esse dado, podemos reescrever a fórmula da seguinte maneira:
Frequência ou tempo das colisões
Se tivermos a velocidade das partículas podemos descobrir o tempo médio entre um choque e outro (), pois
Se dividirmos os dois lados por temos então o tempo:
Ou a frequência de choques, quantas vezes eles se chocam por segundo, se lembrarmos que:
Daí temos como relacionar também com a frequência, basta invertermos a equação:
Então, por exemplo, se tivermos uma amostra de gás hidrogênio a uma temperatura de e seu livre caminho médio nessa condição é de . Sabendo que existem cerca de 50 átomos de hidrogênio por centímetro cúbico e que o diâmetro de um átomo de hidrogênio é da ordem de . Qual a frequência de choques nessa amostra?
Massa molar do hidrogênio:
Bom, nós já temos o livre caminho médio, podemos achar a velocidade e jogar na fórmula:
Para achar a velocidade:
Com isso, achamos :
Pronto, já vimos bastante coisa, agora mãos à obra!
Livre Caminho Médio
Como Calcular?
Frequência ou tempo das colisões
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 242. x-y 18
Calcule a velocidade média quadrática de átomos de hélio a . A massa molar dos átomos de hélio é .
Passo 1
Para descobrirmos a velocidade quadrática média de um gás, vamos usar a fórmula
Substituindo os valores dados no enunciado e usando
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 242. x-y 21
Calcule a velocidade média quadrática de uma molécula de nitrogênio a . A massa molar da molécula de nitrogênio é . A que temperatura a velocidade média quadrática é metade desse valor e o dobro desse valor?
Passo 1
Para calcular a velocidade quadrática médias, vamos usar a fórmula que aprendemos
Substituindo os valores na fórmula e lembrando de passar a temperatura para kelvin e usando
Passo 2
Metade de é , então temos
Assim,
Passo 3
o dobro de é , assim
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 ,Rio de Janeiro: LTC , 2008, x-y 11
A menor temperatura disponível no espaço sideral é Qual é a velocidade média quadrática de moléculas de hidrogênio a essa temperatura?
Massa molar do
Passo 1
Essa questão é bem tranquila. Basta a gente aplicar a equação:
Precisamos só ter cuidado com uma coisa: As unidades. O valor de está expresso por unidades do SI, mas o valor da massa molar do hidrogênio não! Vamos converter:
Logo, aplicando esse valor e os do enunciado na equação:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 242. x-y 28
O livre caminho médio das moléculas de nitrogênio a e é . Nessas condições de temperatura e pressão existem . Qual é o diâmetro das moléculas?
Passo 1
O problema nos fornece o caminho livre médio , e a quantidade de mólecula por centímetro cúbico e pede o diâmetro das moléculas, certo?
Então precisamos apenas aplicar a fórmula que aprendemos
Isolando o diâmetro, temos
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 242. x-y 29
A concentração de moléculas na atmosfera a uma altitude de está em torno de . Supondo que o diâmetro das moléculas é , determine o livre caminho médio Explique se o valor previsto tem significado físico.
Passo 1
Vimos uma fórmula para calcular o livre caminho médio quando o problema fala do diâmetro e da quantidade de moléculas por centímetro cúbico, então vamos usá-la
Substituindo os valores dados pelo o enunciado, temos
Passo 2
Nessa altura a ar na atmosfera fica mais rarefeito, e por isso faz sentido físico o caminho livre médio entre as moléculas ser tão grande, pois quanto mais alto, mais rarefeito será a atmosfera e assim mais difícil ocorrer uma colisão entre as moléculas.
Resposta
Exercício Resolvido #6
PUC-RIO – 3ª Prova – 2010.2
Determine a velocidade média quadrática de uma molécula de oxigênio a . A massa molar do gás oxigênio é .
Passo 1
Para determinar a velocidade média quadrática, vamos lembrar de sua definição:
Passando a temperatura e a massa molar para o S.I, e adotando , temos:
Resposta
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 242. x-y 31
Em um certo acelerador de partículas, prótons se movem em uma trajetória circular de de diâmetro em uma câmara evacuada cujo gás residual está a e a uma pressão de Calcule o número de moléculas do gás por centímetro cúbico com esta pressão. Qual é o livre caminho médio das moléculas do gás se o diâmetro das moléculas é ?
Passo 1
Temos um gás ideal e queremos achar a quantidade de moléculas por centímetro cúbico, sabendo sua pressão e temperatura. Isso lembra uma fórmula que usamos muito a equação dos gases ideiais
Onde podemos reescrevê-la de forma a ficarmos com número de mols por volume
Sabendo que podemos achar o número de moléculas de pelo número de mols, pois
Então temos que
Agora só falta temos a pressão em para podermos resolver a questão, como
Então a nossa pressão será
Bom, chegamos no que queríamos, então vamos substituir os dados que temos e , sendo que e são constantes, assim
Convertendo pra
Passo 2
Agora é só aplicar a fórmula de caminho livre médio que aprendemos
Vamos usar agora e , pra no final ter o em metros.
Resposta
Exercício Resolvido #8
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 242. x-y 24
A e , a massa específica de um gás é . Determine para as moléculas do gás. Determine a massa molar do gás.
Passo 1
Temos que calcular a velocidade quadrática média, porém diferente dos outro exercícios temos apenas a pressão e a massa específica, pois isso vamos usar a fórmula:
Lembrando que no a massa específica é em e a pressão em , então temos que
E
Agora podemos substituir na fórmula
Passo 2
Agora que sabemos a velocidade quadrática média, podemos usar a fórmula
Para descobrirmos quanto vale a massa molar desse gás
Assim
Resposta
Exercício Resolvido #9
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 242. x-y 32
A e a uma pressão de , os caminhos livres médios do argônio e do nitrogênio são e . Determine a razão entre o diâmetro de um átomo de e o de uma molécula de . Qual é o livre caminho médio do argônio a e e a e ?
Passo 1
Como queremos a razão entre os diâmetros, vamos dividir a equação do caminho livre médio
Dividindo elas, chegamos em
Como argônio e nitrogênio esão submetidos a mesma pressão e temperatura então
Assim
Assim
Substituindo os valores dos livres caminhos médio
Passo 2
Como vimos no exercício anterior
Podemos substituir isso na equação do livre caminho médio e chegamos em
Agora, para simplificar nossas contas já que temos os dados do caminho livre médio para o caso em que e, podemos Dividir a equação do livre caminho médio no estado pela do estado .
Onde
Dividindo as equações chegamos em
Então substituindo os valores que temos
Passo 3
Utilizando da fórmula que chegamos no item anterior temos
Mas agora os estado dois mudou
Substituindo na fórmula