Exercícios de Cinética dos Gases - Lista de Exercícios Resolvida
Questão 1
A e a uma pressão de , os caminhos livres médios do argônio e do nitrogênio são e . Determine a razão entre o diâmetro de um átomo de e o de uma molécula de . Qual é o livre caminho médio do argônio a e e a e ?
Ver solução completaQuestão 2
Calcule a velocidade média quadrática de uma molécula de nitrogênio a . A massa molar da molécula de nitrogênio é . A que temperatura a velocidade média quadrática é metade desse valor e o dobro desse valor?
Ver solução completaQuestão 3
O livre caminho médio das moléculas de nitrogênio a e é . Nessas condições de temperatura e pressão existem . Qual é o diâmetro das moléculas?
Ver solução completaQuestão 4
A e , a massa específica de um gás é . Determine para as moléculas do gás. Determine a massa molar do gás.
Ver solução completaQuestão 5
Em um certo acelerador de partículas, prótons se movem em uma trajetória circular de de diâmetro em uma câmara evacuada cujo gás residual está a e a uma pressão de Calcule o número de moléculas do gás por centímetro cúbico com esta pressão. Qual é o livre caminho médio das moléculas do gás se o diâmetro das moléculas é ?
Ver solução completaQuestão 6
Determine a velocidade média quadrática de uma molécula de oxigênio a . A massa molar do gás oxigênio é .
Ver solução completaQuestão 7
A menor temperatura disponível no espaço sideral é Qual é a velocidade média quadrática de moléculas de hidrogênio a essa temperatura?
Massa molar do
Ver solução completaQuestão 8
A concentração de moléculas na atmosfera a uma altitude de está em torno de . Supondo que o diâmetro das moléculas é , determine o livre caminho médio Explique se o valor previsto tem significado físico.
Ver solução completaQuestão 9
Calcule a velocidade média quadrática de átomos de hélio a . A massa molar dos átomos de hélio é .
Ver solução completaQuestão 10
Um cilindro de oxigênio hospitalar com volume de , à temperatura ambiente (), contém à pressão de . (A massa molar das moléculas de é .)
Supondo o gás ideal, determine quantos mols de o cilindro contém.
Qual é a velocidade quadrática média das moléculas de ?
Calcule o volume médio por molécula de , e, a partir dele, estime a distância média entre essas moléculas.
Ver solução completaQuestão 11
Titã, o maior satélite de Saturno, possui uma densa atmosfera de nitrogênio (). Em sua superfície a pressão é vezes a pressão atmosférica terrestre e a temperatura é .
Quantas moléculas por métro cúbico há na atmosfera da superfície de Titã?
Qual é a velocidade quadrática media dessas moléculas? (a massa molar das moléculas de é )
Ver solução completaQuestão 12
Qual é a origem do fator na equação ?
- Ele é uma aproximação para .
- Ele é obtido pela comparação das unidades de pressão e de massa específica.
- Ele está relacionado ao número de dimensões do espaço.
- Ele surge da integração de para obter-se a média.
- Nenhuma das respostas anteriores.
Questão 13
O livre caminho médio de uma molécula de um gás diatômico a uma determinada pressão é de . De quanto será o novo livre caminho médio se dobrarmos a concentração deste gás?
Ver solução completa
Questão 14
(Capítulo 19.Exercícios – Ex. 6) Um gás passa por dois processos. No primeiro, o volume permanece constante a e a pressão cresce de até . O segundo processo é uma compressão até o volume sob pressão constante de . a) Desenhe um diagrama mostrando esses dois processos. b) Calcule o trabalho total realizado pelo gás nos dois processos.
Ver solução completaQuestão 15
Um recipiente é preenchido por uma mistura de gás Hélio (moléculas leves) e gás Oxigênio (moléculas pesadas). Um termômetro mede para essa mistura a temperatura de 22 °C. Quais moléculas de gás têm a maior velocidade média?
- É o mesmo para ambos os gases porque as temperaturas são as mesmas.
- As moléculas de Oxigênio, porque elas são diatômicas.
- As moléculas de Oxigênio, porque elas têm maior massa.
- As moléculas de Hélio, porque elas têm menor massa.
- E) As moléculas de Hélio, porque elas são monatômicas.
Questão 16
Se a temperatura de um gás ideal se duplica mantendo a pressão constante, ao atingir o equilíbrio térmico a velocidade quadrática média das moléculas:
- Cresce por um fator 4.
- Permanece constante.
- Cresce por um fator .
- Cresce por um fator 2.
- Diminui por um fator 2.
Questão 17
. A massa de um mol de oxigênio é de e de nitrogênio é de . As moléculas destes gases, em equilíbrio termodinâmico em uma mesma sala, têm:
energias cinéticas médias iguais, mas as moléculas de nitrogênio são mais rápidas em média.
energias cinéticas médias iguais, mas as moléculas de oxigênio são mais rápidas em média.
energias cinéticas médias e velocidades médias iguais.
velocidades médias iguais, mas as de oxigênio têm energia cinética média mais alta.
velocidades médias iguais, mas as de nitrogênio têm energia cinética média mais alta.
Ver solução completaQuestão 18
Um recipiente é preenchido com uma mistura de gases de hélio (moléculas leves) e oxigênio (moléculas pesadas). A temperatura dentro do recipiente é . Quais moléculas de gás têm a maior velocidade média?
A) É o mesmo para ambos os gases porque as temperaturas são as mesmas.
B) As moléculas de oxigênio porque são diatômicas.
C) As moléculas de oxigênio porque são mais pesadas.
D) As moléculas de hélio porque são menos pesadas.
E) As moléculas de hélio porque são monatômicas.
Ver solução completaQuestão 19
Um gás ideal confinado sofre um processo isobárico no qual sua temperatura diminui até que . O que acontece com o livre caminho médio das moléculas do gás nesse processo?
A) cai pela metade
B) nada, ele fica igual
C) dobra
D) aumenta mas não chega a dobrar
E) cai para um valor maior que a metade do inicial
Ver solução completaQuestão 20
Um pesquisador quer estudar o comportamento termodinâmico de sólidos através de uma simulação de computador. Ele modela um sólido como uma rede cristalina de N átomos idênticos ligados aos seus vizinhos por molas ideais. Para testar se sua simulação está bem feita, ele calcula a energia interna do seu sólido. Qual o valor que ele espera encontrar?
(a) Eint = (1/2)NkBT.
(b) Eint = NkBT.
(c) Eint = (3/2)NkBT.
(d) Eint = (5/2)NkBT.
(e) Eint = 2NkBT.
(f) Eint = 3NkBT.
Ver solução completaQuestão 21
A energia cinética molecular média de um gás pode ser determinada conhecendo-se somente:
a) O número de moléculas no gás.
b) O volume do gás.
c) A pressão no gás.
d) A temperatura do gás .
e) O volume, pressão e temperatura do gás.
Ver solução completaQuestão 22
Considere os seguintes gases comuns em nossa atmosfera: (i) Nitrogênio, diatômico com 28g/mol; (ii) Oxigênio, diatômico com 32 g/mol; e (iii) Argônio, monoatômico com 40 g/mol. Suponha que estes gases estejam em condições de volume, temperatura e pressão nas quais possam ser considerados gases ideais. Os gases estão à mesma temperatura. Responda as questões 1 e 2 abaixo. Considere uma mistura contendo massas iguais de cada um desses gases. Como se relacionam a energia cinética média de translação por molécula (ε) e a energia térmica (E) de cada gás?
A) ε N2 = ε O2 = ε Ar e EN2 = EO2 = EAr
B) ε N2 = ε O2 = ε Ar e EN2 > EO2 > EAr
C) ε N2 = ε O2 > ε Ar e EN2 > EO2 > EAr
D) ε N2 = ε O2 > ε Ar e EN2 = EO2 = EAr
E) ε N2 > ε O2 > ε Ar e EN2 > EO2 > EAr
Ver solução completaQuestão 23
Considere os seguintes gases comuns em nossa atmosfera: (i) Nitrogênio, diatômico com 28g/mol; (ii) Oxigênio, diatômico com 32 g/mol; e (iii) Argônio, monoatômico com 40 g/mol. Suponha que estes gases estejam em condições de volume, temperatura e pressão nas quais possam ser considerados gases ideais. Os gases estão à mesma temperatura. Considere as seguintes afirmativas:
(I) As moléculas destes gases possuem a mesma velocidade quadrática média.
(II) As moléculas de Argônio tem, em média, velocidade menor que as de Oxigênio, que são em média, por sua vez, mais lentas que as moléculas de Nitrogênio.
(III) O gás que possui as moléculas com a maior energia cinética translacional média é o Argônio, pois possui maior massa molar.
A(s) afirmativa(s) CORRETA(S) é(são):
a) I
b) I e II
c) II
d) III
e) I e III
Ver solução completaQuestão 24
A concentração de um gás ideal (número de moléculas por volume) no interior de um reservatório é mantida constante, enquanto sua temperatura varia. Se a temperatura do gás dobra, o livre caminho médio irá:
a) O livre caminho médio não irá variar nessas condições.
b) Dobrar de seu valor inicial.
c) Reduzir à metade do seu valor inicial.
d) Reduzir a um quarto do seu valor inicial.
e) Não podemos afirmar o que vai acontecer, pois depende do número de graus de liberdade que o gás possui.
Ver solução completaQuestão 25
Um balão de contém de hélio a . Sabendo que a massa molar do hélio é de , a velocidade quadrática média de um átomo de hélio nestas condições é de:
- /s
Questão 26
Uma caixa isolada termicamente contém dois compartimentos separados por uma membrana fina. Os dois compartimentos contêm o mesmo gás monoatômico, porém nas condições indicadas na figura ao lado. Sendo a velocidade quadrática média e a energia térmica total, podemos afirmar:
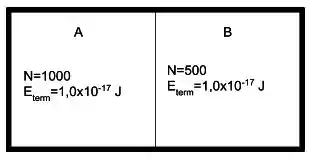
- ,
- ,
- ,
- ,
- ,
Questão 27
Se quatro moléculas estao se movendo com uma velocidade escalar de 2 respectivamente, a velocidade quadrática média das moléculas é aproximadamente:
Questão 28
Dos cinco gases ideais, todos com o mesmo número de moléculas, e com velocidades médias v e diâmetros moleculares d mostrados a seguir, qual é o gás com maior número de colisões por unidade de tempo?
Escolha uma:
Questão 29
Aquece-se uma certa massa de gás ideal a volume constante desde . A razão entre a energia cinética do gás a é mais bem expressa por:
- 3/4
- 27/127
- 4/3
- 1/2
- 1
Questão 30
Um feixe de moléculas idênticas de massa m e velocidade está direcionado para uma parede, em um ângulo com a normal à parede. O feixe possui n moléculas por unidade de volume e atinge a parede sobre uma área dA, como mostrado na figura. Qual é a pressão que o feixe exerce sobre a parede?
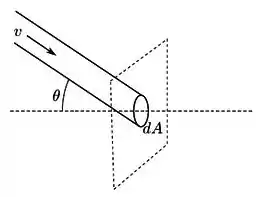
(a) .
(b).
(c) dA.
(d) .
(e).
Ver solução completaQuestão 31
Analise as afirmações abaixo.
I) A pressão dos gases se deve à variação da energia cinética das moléculas ao se chocarem com as paredes do recipiente.
II) Se as moléculas de gás de hidrogênio e oxigênio, em volumes distintos, têm mesma velocidade média quadrática média podemos afirmar que a temperatura do hidrogênio é maior.
III) A pressão dos gases se deve à variação de momento das moléculas ao se chocarem com as paredes do recipiente.
IV) A pressão dos gases se deve à força de repulsão entre as moléculas.
V) Se as moléculas de gás de hidrogênio e oxigênio, em volumes distintos, têm mesma velocidade média quadrática média podemos afirmar que a temperatura do oxigênio é maior.
São verdadeiras:
- II e IV.
- III e V
- II, III e IV
- Apenas III
- Apenas V
- II e V
Questão 32
Considere uma sala com as dimensões de e inicialmente com as janelas e portas fechadas, de modo que não há troca de moléculas.
- Determine o número de moléculas de ar na sala à pressão atmosférica e a
- Determine a massa de ar, assumindo que o ar consiste de moléculas diatômicas de massa molar
- Determine a
- Considere agora uma outra sala com as mesmas dimensões situada numa cidade a de altitude. Nessa altitude, a pressão atmosférica é próxima a Sendo a temperatura ambiente os mesmos , o valor das moléculas é maior, menor ou igual ao calculado em Explique.
Constantes:
Ver solução completaQuestão 33
Um gás de moléculas de nitrogênio () ocupa um volume à temperatura de . Sabe-se que existem no volume ocupado pelo gás. Considere o gás ideal (dado: de tem massa igual a ).
- Determine o número de mols da amostra.
- Determine a energia cinética média (translação + rotação) por molécula do gás.
- Determine, a partir da energia cinética média de translação, a velocidade quadrática média das moléculas do gás.
- Esboce o diagrama do processo termodinâmico e obtenha, em função de , e , o trabalho realizado pelo gás e o calor fornecido ao gás nesse processo.
O gás, nas mesmas condições iniciais acima, é agora submetido a uma expansão em que a pressão aumenta linearmente com o volume. A pressão e o volume no estado final são duas vezes maiores que no inicial ( e ).
Dados:
Ver solução completaQuestão 34
Dois recipientes separados de gás são isolados termicamente do exterior, mas divididos por uma parede fina que é boa condutora de calor (fig). Os dois recipientes são rígidos. Um mol de gás Hélio ) a 0°C é injetado no recipiente direito, e um mol de gás Nitrogênio a 100°C é injetado no recipiente esquerdo. Qual será a temperatura após o equilíbrio térmico ser atingido?
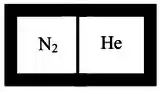
A)
B)
C)
D)
E)
Ver solução completaQuestão 35
Determine a velocidade média quadrática de uma molécula de oxigênio a . A massa molar do oxigênio é .
Ver solução completaQuestão 36
Enquanto 0,305 mol de um gás ideal passam por uma compressão isotérmica a , de trabalho é realizado sobre ele pelo meio ambiente. a) Se a pressão final é , qual é a pressão inicial? (b) Desenhe um diagrama do processo.
Ver solução completaQuestão 37
Um gás ideal é mantido em um recipiente rígido. Quando sua temperatura é 100 K, o caminho livre médio das moléculas de gás é λ. Qual será o caminho livre médio das moléculas a 400 K?
A)
B)
C)
D)
E)
Ver solução completaQuestão 38
Três cilindros, I, II e III fechados por um êmbolo móvel, contém amostras idênticas de um mesmo gás ideal. A força F que o êmbolo exerce sobre o gás é ajustada de modo que a pressão e o volume iniciais do gás no interior de todos os cilindros sejam Pa e Va respectivamente. Então o gás contido em cada cilindro sofre um processo distinto descrito abaixo e ilustrado no diagrama PV da Figura ao lado. Todos os processos terminam à mesma temperatura T2.
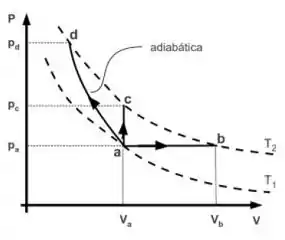
I) O gás do cilindro I é aquecido, e o volume da câmera é alterado, mantendo-se o valor da força F inalterado.
II) O gás do cilindro II é aquecido mantendo-se a posição do êmbolo inalterada.
III) O êmbolo comprime o gás do cilindro III suficientemente rápido para que o calor trocado entre o gás e sua vizinhança seja desprezível.
Qual a relação correta entre as variações das energias internas?
A) ΔE ab
B) ΔE ac
C) ΔE ad =ΔE ac
D) ΔE ad = ΔE ab = ΔE ac
E) ΔE ac
Ver solução completaQuestão 39
Uma caixa contém uma mistura de gás hélio (moléculas leves) e gás oxigênio (moléculas pesadas). Um termômetro dentro da caixa marca 22°C. Qual molécula tem energia cinética média maior?
A) É a mesma para ambas as moléculas já que a temperatura é a mesma
B) As moléculas de oxigênio porque elas são diatómicas
C) As moléculas de oxigênio porque elas são mais pesadas
D) As moléculas de hélio porque elas são mais leves
E) As moléculas de hélio porque elas são monoatómicas
Ver solução completaQuestão 40
Complete a seguinte afirmação: A pressão exercida por um gás ideal monoatômico sobre as paredes do recipiente que contém é proporcional
- à energia cinética média dos átomos por unidade de volume
- à energia cinética média dos átomos e ao volume do recipiente
- à energia cinética média dos átomos, independentemente do volume do recipiente
- à energia térmica do gás, independentemente do volume do recipiente
- ao momento linear médio por unidade de volume
Questão 41
Quando a pressão de um gás ideal diminui isotermicamente até o seu volume dobrar, a velocidade quadrática média das suas moléculas:
a) cai por um fator
b) aumenta por um fator
c) permanece constante
d) dobra
e) cai pela metade.
Ver solução completaQuestão 42
Qual dos valores abaixo está mais próximo do livre caminho médio de uma molécula de um gás rarefeito de nitrogênio a pressão de e a temperatura ambiente? Sabe-se que na pressão atmosférica e na temperatura ambiente, o livre caminho médio dessa molécula é aproximadamente.
Dados:
Ver solução completaQuestão 43
Se a temperatura de uma quantidade fixa de um gás ideal é aumentada, então necessariamente:
- a pressão do gás vai aumentar.
- o volume do gás irá aumentar.
- a velocidade média das moléculas do gás irá aumentar.
- o livre caminho médio irá aumentar.
- todas as opções acima estão corretas.
Questão 44
Segundo a teoria cinética, um gás é constituído por moléculas que se movimentam desordenadamente no espaço do reservatório onde o gás está armazenado. As colisões das moléculas entre si e com as paredes do reservatório são perfeitamente elásticas. Entre duas colisões sucessivas, as moléculas descrevem um movimento retilíneo uniforme a energia cinética de translação das moléculas é diretamente proporcional à temperatura do gás. Com base nessas informações, considere as seguintes afirmativas:
1- As moléculas se deslocam todas em trajetórias paralelas entre si.
2- Ao colidir com as paredes do reservatório, a energia cinética das moléculas é conservada.
3- A velocidade de deslocamento das moléculas aumenta se a temperatura do gás for aumentada.
Assinale a alternativa correta.
- Somente a afirmativa 1 é verdadeira.
- Somente a afirmativa 2 é verdadeira.
- Somente a afirmativa 3 é verdadeira.
- Somente a afirmativa 1 e 2 são verdadeiras.
- Somente a afirmativa 2 e 3 são verdadeiras.
Questão 45
1 - Um gás ideal é comprimido devagar e isobaricamente até a metade de seu volume original. Se a velocidade média quadrática (rms) das moléculas do gás era v, a nova velocidade, após a compressão, é:
Questão 46
. Um gás ideal composto de mol de moléculas diatônicas de massa molar com energia interna é mantido em um recipiente de volume . Calcule a velocidade quadrática média e a pressão nas paredes do recipiente .
Dados
e
. e
. e
. e
. Nenhuma das alternativas
. e
. e
. e
. e
Ver solução completaQuestão 47
Para elevar de para a temperatura de um mol de He (hélio, monoatômico) mantido a volume constante, gasta-se uma quantidade de calor . Para realizar o mesmo procedimento com um mol de (hidrogênio, diatômico) gasta-se uma quantidade de calor . Sejam e as energias cinéticas de translação médias de cada molécula de hélio e hidrogênio, respectivamente, à temperatura . Podemos afirmar que:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 48
Um reservatório contém dois moles do gás , monoatômico e com massa molar , a uma temperatura . Um outro reservatório, idêntico ao primeiro, contém dois moles do gás , diatômico e com massa molar , também a temperatura . Os gases são aquecidos até que ambos atinjam a mesma temperatura . Nestas condições, se comportam como gás ideal. Considere as seguintes afirmações:
I. A energia cinética média de translação das moléculas de é a mesma que das moléculas de , tanto a temperatura como a temperatura .
II. A quantidade de calor fornecida ao para elevar sua temperatura de para foi menor que a necessária para o .
III. A variação da energia interna do é igual a da energia interna do , ao elevar suas temperaturas de para .
IV. O valor médio do quadrado da velocidade das moléculas de é maior que o valor médio do quadrado da velocidade das moléculas de He, tanto a temperatura como a temperatura .
As afirmações corretas são as seguintes:
- I, II e IV
- I e II
- I, II e III
- I e IV