Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Distribuição de Velocidades

Ver Todos os Exercícios

Teoria

Distribuição de velocidades

Beleza, então já sabemos calcular a velocidade quadrática média das moléculas de um gás.

Mas e se quiséssemos saber a velocidade de cada uma das moléculas de um gás?

Como as partículas possuem diferentes velocidades, para representar de forma correta as velocidades, foi criada a função f v , chamada de distribuição de Maxwell-Boltzmann. Que é a porcentagem de partículas que estão naquela velocidade ( f ,   e i x o   y ) versus a velocidade ( v ,   e i x o   x ).

Isso nós podemos ver pelo gráfico de distribuição de velocidades, como esse aqui:

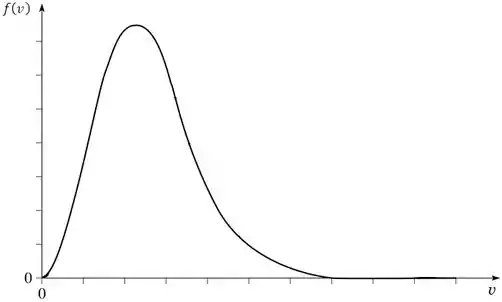
Repare que se somarmos todas as as probabilidades de todas as velocidades temos que encontrar 100%. Matematicamente, a área abaixo da curva tem que dar 1:

∫ 0 ∞ f v d v = 1

Essa curva vem de uma equação bem complicadinha:

f v = 4 π m 2 π k T 3   v 2 e - m v 2 2 k T

Mas não se assuste! Pois em geral, nós só vamos querer saber duas coisas:

  • Qual é a velocidade mais provável;
  • Como esse gráfico varia com a temperatura.

Velocidade mais provável – v m p

A velocidade mais provável é aquela onde a derivada da curva é zero, ou seja, é a velocidade relativa a um pico.

Graficamente:

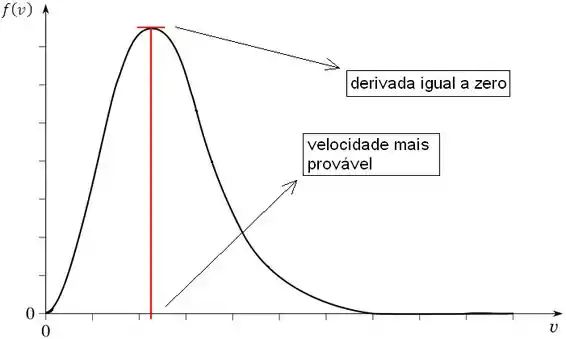
Se for dada a equação da curva, basta calcular a derivada em relação a v e igualar a zero:

d f d v = 0

Que dá, na distribuição de Maxwell-Boltzmann:

v m p = 2 k T m

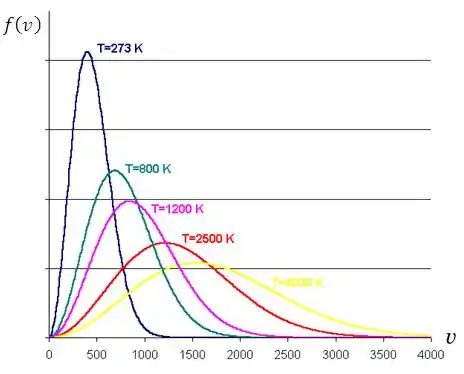
Como o gráfico varia com a temperatura

O que precisamos saber sobre a variação com a temperatura é:

  • Quanto maior a temperatura, mais baixo é o pico e mais larga é a curva.
  • Quanto menor a temperatura, mais alto é o pico e mais estreita é a curva.

Podemos ver esse efeito pelo gráfico:

Então, podemos esquematizar isso da seguinte forma:

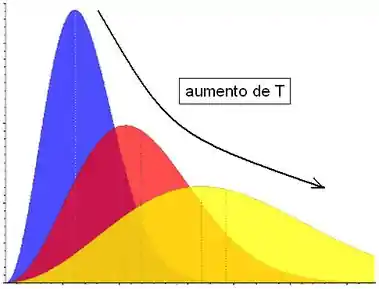
Quanto maior a temperatura, maiores vão ser as velocidades que as moléculas vão conseguir alcançar (gráfico mais para direita).

E como a área embaixo do gráfico tem que ser sempre igual a 1, então quando maior a temperatura, menor vai ser a altura do pico.

Beleza?

Relação entre a velocidade média, quadrática média e a velocidade mais provável

A velocidade média é dada pela fórmula:

v m = ∫ 0 ∞ v   f v d v

Que na equação de Maxwell-Boltzmann dá:

v m = 8 k T π m

A velocidade quadrática média pela fórmula:

v q m = ∫ 0 ∞ v 2   f v d v   = 3 k T m

E a velocidade mais provável, como acabamos de ver, é dada pela fórmula:

v m p = 2 k T m

Repare que, como

3 > 8 π ~ 2,5 > 2

Então:

v q m > v m > v m p

Às vezes, vão te pedir pra achar uma das velocidades e vão te dar o valor de outra. Daí, é só você lembrar da relação entre elas, que é:

v m p = v q m 2 3 = v m 2 . π

Lembrando que, dado um grupo finito de partículas, podemos calcular sua velocidade média e velocidade quadrática média através das fórmulas convencionais:

v m = ∑ i = 0 n v i n

E

v q m = ∑ i = 0 n v i 2 n

Partiu exercitar?

Velocidade mais provável – v m p

Como o gráfico varia com a temperatura

Relação entre a velocidade média, quadrática média e a velocidade mais provável

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , Rio de Janeiro: LTC , 2008, x-y 09

As moléculas de um gás com seis partículas têm velocidades representadas pelos vetores:

v → 1 = 20 i ^ + 30 j ^   m / s

v → 2 = - 40 i ^ + 70 j ^   m / s

v → 3 = - 80 i ^ - 10 j ^   m / s

v → 4 = 60 i ^ - 20 j ^   m / s

v → 5 = - 50 j ^   m / s

v → 6 = 40 i ^ - 20 j ^   m / s

Determine:

a v → m e d ;

b v m e d ;

c v r m s .

Passo 1

a   Para determinar o vetor velocidade média, precisamos somar cada termo em x e em y separadamente e dividir pelo número de moléculas, vamos começar com os termos em x :

v m e d x = [ 20 - 40 - 80 + 60 + 40 ] ( i ^ ) 6 = 0

Em y , temos:

v m e d y = [ 30 + 70 - 10 - 20 - 50 - 20 ] ( j ^ ) 6 = 0

Portando, temos:

v → m e d = 0

Passo 2

b Para determinar a velocidade escalar média, temos que calcular o módulo da velocidade de cada uma das moléculas:

v 1 = 20 2 + 30 2 = 1300 ≈ 36,1

v 2 = ( - 40 ) 2 + 70 2 = 6500 ≈ 80,6

v 3 = ( - 80 ) 2 + ( - 10 ) 2 = 6500 ≈ 80,6

v 4 = 60 2 + ( - 20 ) 2 = 4000 ≈ 63,2

v 5 = ( - 50 ) 2 = 2500 ≈ 50

v 6 = 40 2 + ( - 20 ) 2 = 2000 ≈ 44,7

Somando e dividindo por 6 , acharemos a média!

v m e d = 36,1 + 80,6 + 80,6 + 63,2 + 50 + 44,7 6 = 59,2   m / s

Passo 3

c   Para determinar a velocidade quadrática média, precisamos lembrar da seguinte relação:

v r m s = ∑ i = 0 n v i 2 n

Ou seja:

v r m s = v 1 2 + v 2 2 + v 3 2 + v 4 2 + v 5 2 + v 6 2 6

v r m s = 1300 + 6500 + 6500 + 4000 + 2500 + 2000 6

v r m s = 3800

v r m s = 61,6   m / s

Resposta

a v → m e d = 0

b   v m e d = 59,2   m / s

c v r m s = 61,6   m / s

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 242. x-y 33

Dez partículas estão se movendo com as seguintes velocidades: quatro a 200   m / s , duas a 500   m / s   e quatro a 600   m / s . Calcule suas velocidades a   médias e b   média quadrática. c   v r m s é maior que v m é d ?

Passo 1

a   A fórmula da velocidade média para um sistema com número finito de partículas é

v m = ∑ i = 0 n v i n

Então temos

v m = 4.200 + 2.500 + 4.600 10

v m = 420   m / s

Passo 2

b   Já a fórmula da velocidade quadrática média é

v q m = ∑ i = 0 n v i 2 n

Assim,

v q m = ( 4.200 2 + 2.500 2 + 4.600 2 ) 10

v q m = 458,25   m / s

Passo 3

c   Como

v r m s = v q m

Então temos que

v r m s > v m

Resposta

a v m = 420   m / s

b   v q m = 458,25   m / s

c   S i m

Exercício Resolvido #3

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 243. x-y 36

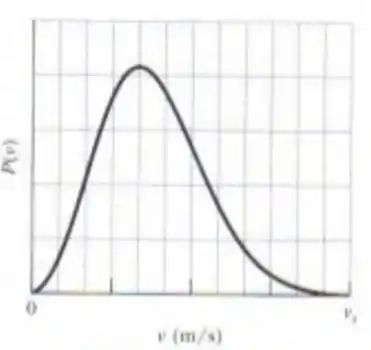
A figura abaixo mostra a distribuição de probabilidade da velocidade das moléculas de uma amostra de nitrogênio. A escala do eixo horizontal é definida por v s = 1200   m / s . Determine a   a temperatura do gás e b   a velocidade média quadrática das moléculas.

Dado: massa molar do nitrogênio M = 28   g / m o l

Passo 1

a   Par determinarmos a temperatura, precisamos descobrir qual é a velocidade mais provável, e faremos isso atráves do gráfico, a abcissa do ponto mais alto é o valor da velocidade mais provável.

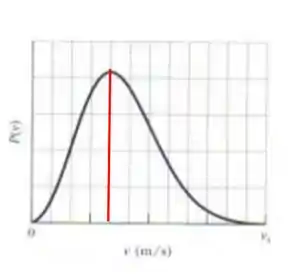
Para descobrir o ponto no eixo x que a reta vermelha representa, vamos ter que descobrir quanto cada quadrado vale.

Para isso vamos dividir o valor de v s pela quantidade de quadrado até v s , assim temos

v q u a d r a d o = v s n

Como temos 12   quadrados

v q u a d r a d o = 1200 12

v q u a d r a d o = 100   m / s  

Então como a reta vermelha está no quarto quadrado, temos que

v m p = 4.100  

v m p = 400   m / s  

Passo 2

Agora que sabemos a velocidade mais provável, podemos utilizar a fórmula dela para descobrirmos a temperatura

v m p = 2 k B T m

Como não sabemos a massa m da amostra apenas a massa molar M = 28   g / m o l ,

Podemos usar que

k B = R N a

Então

v m p = 2 R T M

Isolando a temperatura agora, chegamos em

T = 1 2 . v m p 2 . M R

Substituindo pelos valores que temos

T = 1 2 . 400 2 . 28.10 - 3 8,3

T = 270   K

Passo 3

c   Para isso vamos usar a relação entre as velocidade

v p = v q m 2 3

v q m = v p . 3 2

v q m = 400 . 1,5

v q m = 489,89   m / s

Resposta

a   T = 270   K

b   v q m = 489,89   m / s

Exercício Resolvido #4

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 2 , 8º ed. Rio de Janeiro: LTC , 2008, pp 243-38

Dois recipientes estão à mesma temperatura. O primeiro contém gás à pressão p 1 , de massa molecular m 1 e velocidade média quadrática v r m s 1 . O segundo contém gás à pressão 2,0 . p 1 , de massa molecular m 2 e velocidade média v m é d 2 = 2,0 . v r m s 1 . Determine a razão m 1 / m 2 .

Passo 1

O problema nos deu uma relação entre a velocidade média do gás 2 e a velocidade quadrática média do gás 1 então vamos escrever essa relação

v m é d 2 = 2,0 . v r m s 1

Substituindo pelas fórmulas que conhemos temos

8 k B T π m 2 = 2 . 3 k B T m 1

Onde m representa a massa molecular da substância que constitui o gás.

Cortando e tirando as raízes, chegamos em

m 1 m 2 = 3 2 . π

m 1 / m 2 ≅ 4,7

Resposta

m 1 / m 2 ≅ 4,7

Exercício Resolvido #5

UFRJ – 1ª Prova – 2014.2

A figura mostra duas curvas representando possíveis distribuições esfericamente simétricas de velocidades, em três dimensões, das moléculas de uma M E S M A   amostra de gás segundo a distribuição de velocidades de Maxwell.

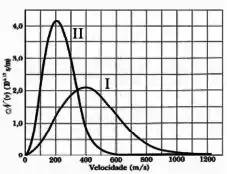
Considere as seguintes afirmativas:

I A curva I demonstra a situação coma temperatura mais alta.

I I Apesar das curvas serem diferentes, as áreas sob cada curva são iguais.

I I I A fração de moléculas com velocidade superior à 300 m / s é maior para a curva I I .

I V Em ambas as curvas a velocidade mais provável para uma molécula escolhida ao acaso é menor que as respectivas velocidades médias.

As afirmações corretas são:

a   I ,   I I   e   I I I .

b   I ,   I I   e   I V .

c   I ,   I I I   e   I V .

d   I   e   I V .

e   Todas.

Passo 1

Vamos analisar cada afirmação:

I - Correta, quanto maior a temperatura, mais achatada vai ser a curva!

I I - Correta! Essa é um pouco mais difícil de entender, mas vamos lá:

As funções de distribuição de velocidades têm no eixo y , probabilidades. São funções de probabilidade, ok?

Então, são sempre números quebrados: 0,3 , 0,4 , 0,5 .

Se quisermos calcular a área sob a curva, o que acharemos?

Acharemos a soma de todas as probabilidades da amostra! E qual é a soma de todas as probabilidades? 100 % , ou 1!

Então, não importa o formato da curva, sempre dará 1. Ou, matematicamente:

∫ f v = 1

Onde f ( v ) é a função de distribuição das probabilidades.

Passo 2

I I I - Essa é bem tranquila. Dê uma olhada no gráfico. Achou o ponto que tem velocidade 300   m / s ?

Então, trace um linha vertical assim:

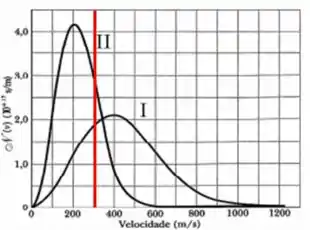
Agora veja a área abaixo do gráfico 2 e a área abaixo do gráfico 1, analisando apenas as partes dos gráficos que estão depois da linha vermelha.

Como vimos, a área sob o gráfico nos dá a probabilidade total. Como a área de 2 é menor que a área de 1, a probabilidade total também de 2 também é menor.

Uma probabilidade maior acaba levando a um maior número de moléculas, então, essa afirmativa é falsa. Na verdade, a fração maior pertence ao gráfico 1.

Passo 3

I V - Verdade! Basta olhar na nossa teoria a relação entre a velocidade mais provável de um gás e a sua velocidade média. A relação é:

v p = v q m 2 3

Como

2 3 < 1   → v p < v q m  

Então a velocidade mais provável de uma molécula de um gás é sempre menor que a sua velocidade média.

Resposta

b

Exercício Resolvido #6

UNICAMP – 2ª Prova – 2007.2

A distribuição de velocidades escalar para as moléculas de um mol de certa substância é dada pela função:

P v = - 6 v 2 + 6 v   s e   0 < v < 1,0   k m / s                 0               s e   0 > v   e   v > 1,0   k m / s

a   De acordo com essa distribuição de velocidades, qual é a velocidade mais provável?

b   Qual a velocidade quadrática média das moléculas?

c   Tratando a substância como um gás ideal monoatômico de massa molar M = 20 g , calcule a temperatura da substância em K para esta distribuição.

Dados:

k = 1,38 × 10 - 23   J / K

N A = 6,02 × 10 23

Passo 1

a   Bom, P v é uma função probabilidade. Então, a velocidade mais provável vai ser aquela que tiver a maior probabilidade em P v , isso é, vai ser aquela que vai gerar um pico no gráfico de P v .

Mas como você pode ver, P ( v ) tem dois intervalos: de 0 a 1 a função é uma parábola e de 1 pra cima o valor do gráfico é 0. Então, o gráfico com as duas partes ficará assim:

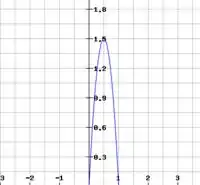
Montando o gráfico:

Basicamente só precisamos desenhar a parábola. Descobrindo as raízes:

P v = 0   ↔   - 6 v 2 + 6 v = 0   ↔ v - v + 1 = 0 ↔ v = 0   ou v = 1

Show? São as duas raízes.

Botamos lá encima.

Daí para achar a velocidade mais provável é só pegar a velocidade que gera o pico da parábola. Como ver isso? Bem, o pico da parábola fica bem no meio da parábola...

Então, como as raízes são 0 e 1 , o pico ficará no meio delas. No caso:

v p = 0,5   k m / s

E essa é a velocidade mais provável (:

Passo 2

b   Vamos nos lembrar da relação entre a velocidade quadrática média e a a velocidade mais provável:

v p = v q m 2 3 → v q m = v p 3 2

Então:

v q m = 0,5 . 3 2 ≅ 0,61   k m / s

Passo 3

c   Vamos usar o valor da velocidade mais provável e a formula que usa a temperatura:

v p = 2 k T m

Dai é só isolar T :

v p 2 . m 2 k = T

Só que esse m é a massa de uma molécula. Precisamos calcular esse m já que não deram pra gente. Mas como nos deram a massa molar e a constante de Avogadro:

m = M N A = 20 x 10 - 3 k g / m o l 6,02 × 10 23 / m o l ≅ 3,32 x 10 - 26   k g

Jogando tudo na equação:

T = v p 2 m 2 k

T = 500 2 ⏟ 500 m / s = 0,5 k m / s . 3,32 x 10 - 26 2.1,38 x 10 - 23

T ≅ 300,7 K

Resposta

a   v p = 0,5   k m / s

b   v q m ≅ 0,61   k m / s

c   T ≅ 300,7 K

Exercícios de Livros Relacionados

A 20° C e a uma pressão de 750t o r r , o livre caminho médio do argônio ( A r ) é λ A r = 9,9.10 - 6c m e o livre caminho médio da molécula de nitrogênio ( N 2 ) é λ N 2 = 27,5.10 - 6c m . (a) Determ
Um gás ideal sofre uma compressão adiabática de p = 1,0a t m , V = 1,0.10 6L , T = 0,0 ° C para p = 1,0.10 5 a t m , V = 1,0.10 3L . (a) O gás é monoatômico, diatômico ou poliatômico? (b) Qual é a tem
A velocidade mais provável das moléculas de um gás quando está a uma temperatura T 2 é igual à velocidade média quadrática das moléculas do gás quando está a uma temperatura T 1 . Calcule a razão T 2
A que temperatura a velocidade média quadrática (a) do H 2 (hidrogênio molecular) e (b) do O 2 (oxigênio molecular) é igual à velocidade de escape da Terra (Ver tabela 13 - 2 )? A que temperatura a ve
A figura mostra a distribuição de probabilidade da velocidades das moléculas de uma amostra de nitrogênio. A escala do eixo horizontal é definida por v s = 1200m / s . Determine (a) a temperatura do g