SUB de Física 1 da UTFPR - 2022.2
Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades (Figura 1). A barra possui de comprimento e a massa de , enquanto as bolas possuem cada uma e podem ser tratadas como partículas pontuais. Ache o momento de inércia desse sistema em relação a cada um dos seguintes eixos:
c) um eixo paralelo à barra e que passa por ambas as bolas

Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades (Figura 1). A barra possui de comprimento e a massa de , enquanto as bolas possuem cada uma e podem ser tratadas como partículas pontuais. Ache o momento de inércia desse sistema em relação a cada um dos seguintes eixos:
d) um eixo paralelo à barra e a uma distância de dela.

Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades (Figura 1). A barra possui de comprimento e a massa de , enquanto as bolas possuem cada uma e podem ser tratadas como partículas pontuais. Ache o momento de inércia desse sistema em relação a cada um dos seguintes eixos:
b) um eixo perpendicular à barra e que passa por uma das bolas

Uma pedra esférica de raio , uniforme e maciça e parte do repouso e rola para baixo de uma colina de 30,0 m de altura e inclinação de , como indica a figura 3. A metade superior da colina é áspera o suficiente para fazer a pedra rolar sem deslizar, mas a metade inferior está coberta de gelo e não há atrito.
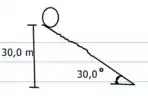
a) Calcule a aceleração da pedra na parte áspera.
b) Calcule a velocidade escalar de translação da pedra quando ela atinge a metade da colina.
c) Calcule a velocidade escalar de translação da pedra quando ela atinge a base da colina.
Ver solução completaUma barra uniforme possui duas pequenas bolas coladas às suas extremidades (Figura 1). A barra possui de comprimento e a massa de , enquanto as bolas possuem cada uma e podem ser tratadas como partículas pontuais. Ache o momento de inércia desse sistema em relação a cada um dos seguintes eixos:
a) um eixo perpendicular à barra e que passa pelo seu centro

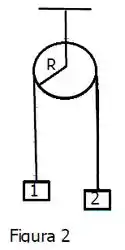
Dois blocos com massas e estão conectados um ao outro por meio de uma corda com massa desprezível que passa por uma polia de massa com formato de um disco rígido de raio (Figura 2). Encontre a aceleração dos blocos e as tensões na corda. (Assuma que não há deslizamento entre a corda e a polia.)