Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Triplas

Ver Teoria
Exercício 41235678910

Enunciado

Calcule a integral tripla

∭ T x 2 d V

Em que T é o tetraedro sólido com vértices 0,0 , 0 , 1,0 , 0 , 0,1 , 0 e 0,0 , 1

Passo 1

Opa, tudo bom?

Vamos lá, temos que achar aquela integral que ele pediu. Vamos começar entendendo como é a cara desse tetraedro. Vamos colocar os pontos no 3 D e ver como vai ficar essa bagunça.

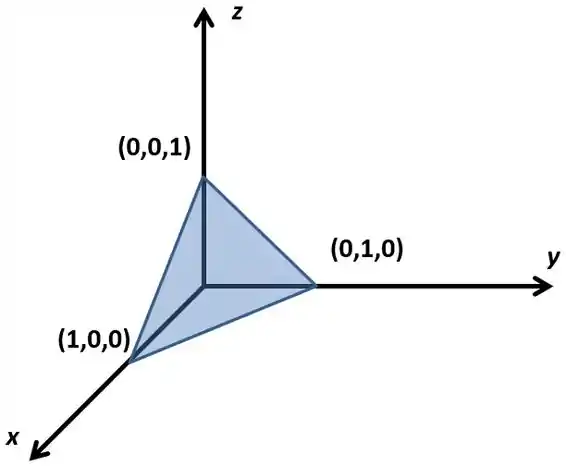
Pela figura conseguimos perceber que o z vai de 0 ao plano, e x y vão ficar limitados a região D que é a base desse tetraedro. A primeira coisa a fazer é achar a equação do plano, a equação do plano vai ser

a x + b y + c z = d

Substituindo os pontos vamos ter, primeiro 1,0 , 0

a = d

Depois 0,1 , 0

b = d

Agora 0,0 , 1

c = d

Então vamos ter

d x + d y + d z = d

Dividindo os dois lados por d , temos:

x + y + z = 1

Isolando z , temos

z = 1 - x - y

Então z vai de 0 até z = 1 - x - y

A região T vai ficar

T = x , y , z ∈ R 3 x , y ∈ D ; 0 ≤ z ≤ 1 - x - y

Falta acharmos D

Passo 2

Agora vamos desenha no plano x y aquela região D

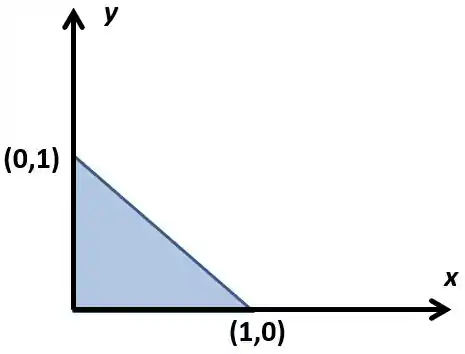
Aqui podemos fazer duas coisas ou limitar x de 0 até a reta ou limitar y de 0 até a reta.

Vamos limitar y . O detalhe aqui é que uma variável vai ser limitada por funções e outra vai ser limitada por números.

Repara que vamos ter y indo de 0 até aquela reta, e x indo de 0 à 1 , falta achar a equação dessa reta que passa por 1,0 e 0,1

A equação da reta é

y = a x + b

Então, substituindo 1,0 na equação, vamos ter

0 = a + b

Agora substituindo 0,1 na equação vamos ter

1 = b

Isso nos diz que

a = - b = - 1

E a equação da reta vai ser

y = - x + 1

Vamos reescrever a região T agora

T = x , y , z ∈ R 3 0 ≤ x ≤ 1 ; 0 ≤ y ≤ - x + 1 ; 0 ≤ z ≤ 1 - x - y

Passo 3

Vamos ver agora como fica a nossa integral

∭ T x 2 d V = ∫ 0 1 ∫ 0 - x + 1 ∫ 0 1 - x - y x 2 d z d y d x

Vamos resolver essa integral

∫ 0 1 ∫ 0 - x + 1 ∫ 0 1 - x - y x 2 d z d y d x

Passo 4

Integrando primeiro em relação a z , temos:

∫ 0 1 ∫ 0 - x + 1 x 2 z 0 1 - x - y d y d x

Substituindo os valores em z , ficamos com

∫ 0 1 ∫ 0 - x + 1 x 2 1 - x - y d y d x =

∫ 0 1 ∫ 0 - x + 1 x 2 - x 3 - y x 2 d y d x

Passo 5

Agora integrando em relação a y ficamos com

∫ 0 1 x 2 y - x 3 y - x 2 y 2 2 0 - x + 1 d x =

Substituindo os valores em y , temo

∫ 0 1 x 2 - x + 1 - x 3 - x + 1 - x 2 - x + 1 2 2 d x =

Podemos dar uma ajeitadinha hehe

∫ 0 1 - x 3 + x 2 + x 4 - x 3 - x 2 x 2 - 2 x + 1 2 d x =

∫ 0 1 - x 3 + x 2 + x 4 - x 3 - x 4 - 2 x 3 + x 2 2 d x =

∫ 0 1 - x 3 + x 2 + x 4 - x 3 - x 4 2 + x 3 - x 2 2 d x =

E isso nos dá:

∫ 0 1 x 4 2 - x 3 + x 2 2 d x

Passo 6

Show, bora integrar esse monstrinho em relação a x

x 5 10 - x 4 4 + x 3 6 0 1 =

1 10 - 1 4 + 1 6 =

6 - 15 + 10 60 =

1 60

Aqui vale um comentário rápido, o gabarito que achamos dessa prova está errado, o resultado final dele é 1 / 24 , mas eu fiz essa integral, que ficou como a do gabarito no Mathematica e o valor deu esse que achamos, eles devem ter errado alguma conta por lá, pode confiar nessa resposta.

Resposta

1 60

Exercícios de Livros Relacionados

a) Resolva o sistema u = 3x + 2y, v = x + 4y , para x e y em termos de u e v. Em seguida, encontre o valor do jacobiano ∂(x, y)/∂(u, v).b) Encontre a imagem pela transformação u = 3x + 2y, v = x +4y d
Calcule as integrais nos Exercícios 7-20.int_1^e int_1^(e^2) int_1^(e^3) (1)/(x y z) d x d y d z
Calcule as integrais nos Exercícios 7-20.int_0^1 int_0^1 int_0^1 (x^2 + y^2 + z^2) d z d y d x
Calcule as integrais nos Exercícios 7-20.int_0^((pi)/(6)) int_0^1 int_(- 2)^3 y s e n (z) d x d y d z
Calcule a integral ∫ 0 4 ∫ x = y 2 x = y 2 + 1 2 x - y 2 d x d y do Exemplo 1 diretamente pela integracao com relacao a x e y para confirmar que seu valor e 2.