Determine a massa do sólido limitado por , , , , cuja densidade no ponto é o produto das coordenadas.
Passo 1
Oiiiii, vamos seguir com nossos estudos uhul!
O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por . Vale lembrar que:
Onde é o diferencial de massa e o de volume. Integrando ambos os lados na região em que o sólido está contido, temos que:
Passo 2
Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.
Temos o plano (que é um plano qualquer) limitado por , e .
Para desenhar esse plano, podemos encontrar os pontos em que ele corta os eixos , e , fazendo, respectivamente, , e .
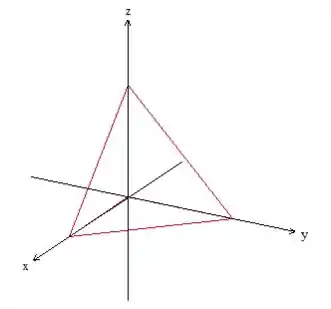
Para você ver mellhor, o sólido é esse aqui:
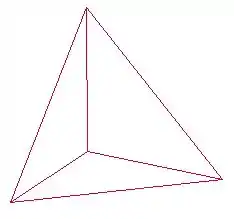
Passo 3
Agora vamos escrever matematicamente essa região. Vamos Escrevê-la como tipo I, limitada em por funções e no plano por uma área .
Na variável , o sólido é limitado embaixo pelo plano e em cima pelo plano , então, podemos escrever:
Depois nos preocupamos com essa região , ok?
Passo 4
Agora vamos levar isso aí para a integral
Agora vamos olhar só para essa integral em relação a
Integrando isso dai em relação a , temos
Substituindo os valores dos limites, temos
Agora, colocando isso na nossa integral em relação à região temos:
Passo 5
Agora vamos escrever matematicamente essa região , que é a projeção do sólido no plano . Olhando o sólido de cima, temos isso aqui.
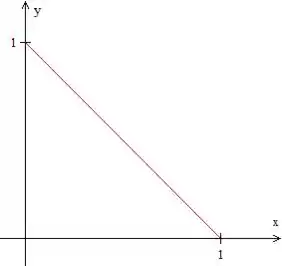
A região de que estamos falando é esse triângulo aí. Para encontrar essa reta, basta fazer na equação do plano:
Essa reta é onde o plano corta o plano . Então, podemos escrever como região do tipo I, entre funções e entre números, temos:
Levando para a integral:
Passo 6
Agora vamos resolver isso aí, começando a olhar pela integral de dentro (em relação a
Vamos então fazer a substituição simples:
Derivando em relação a :
Lembre-se de que nessa integração é visto como constante.
Fazendo a distributiva, temos que
Integrando isso daí em relação a temos:
Substituindo os valores dos limites de integração, ficamos com
Podemos ajeitar isso dai, colocando em evidencia em
Opa, podemos juntar os e somar os expoentes, ficando com
Colocando isso na nossa integral de fora, lembrando que temos multiplicando ela, ficamos com:
Ajeitando o denominador, ficamos com
Tirando as constantes, ficamos com
Passo 7
Ufa, agora que a gente ajeitou essa integral, vamos partir pra cima dela, fazendo uma substituição simples:
Temos então:
Dando um jeitinho nesses sinais de menos e fazendo a distributiva, ficamos com:
Resolvendo essa integral, temos que
Agora, fazendo a substituição, temos