Exercícios de Vigas Compostas - Lista de Exercícios Resolvida
Questão 1
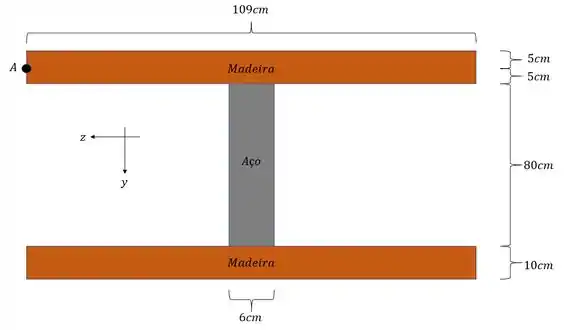
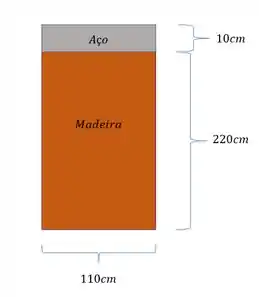
uma peça de madeira foi reforçada com uma barra de ferro como mostras a figura. Usando seus conhecimentos sobre vigas compostas e sabendo que o modulo de elasticidade da madeira é dado por e determine a tensão na extremidade do aço e na interface aço madeira. O momento fletor que age sobe essa peça é de 15KN.m. observe os eixos usados.
Questão 2
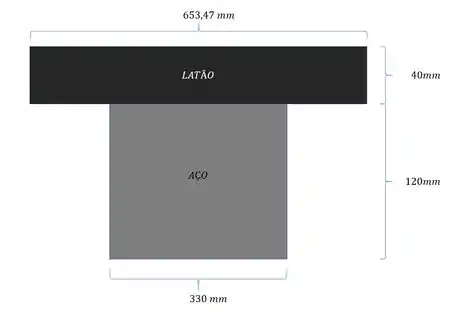
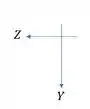
Projetou-se uma passarela com seção transversal como o mostrado na figura. Sabendo que nessa seção da passarela existe a ação de um momento fletor de intensidade 235 KN.m determine o valor da tensão normal na extremidade do latão, na junção latão aço, na junção aço alumínio e na extremidade do alumínio. Atente-se ao sinal arbitrado.
Questão 3
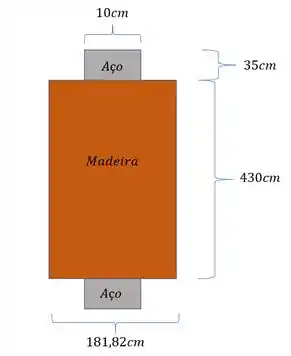
A viga de madeira abaixo foi reforçada com duas hastes de aço como mostrado na figura. Sabendo que a seção aqui mostrada sofre a ação de um esforço de flexão de modulo 127KN.m determine o valor da tensão normal que aparece na extremidade das barras de aço e na interface Aço-madeira. Usar e . Atenção ao eixo utilizado.
Questão 4
A viga composta é feita de aço A-36 e latão vermelho C83400 e tem a seção transversal mostrada na figura. Se for submetida a um momento , determine a tensão máxima no latão e no aço. Determine também a tensão em cada material na junção entre eles.
Dados: , .
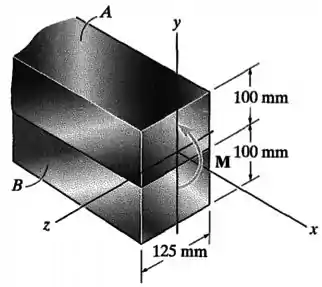
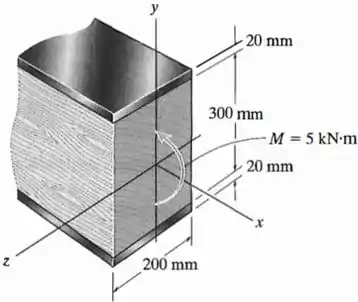
Questão 5
As partes superior e inferior da viga de madeira são reforçadas com tiras de aço, como mostra a figura. Determine a tensão de flexão máxima desenvolvida na madeira e no aço se a viga for submetida a um momento fletor . Trace um rascunho da distribuição de tensão que age na seção transversal. Considere , .
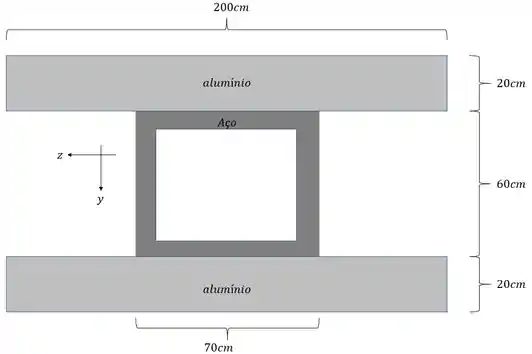
Questão 6
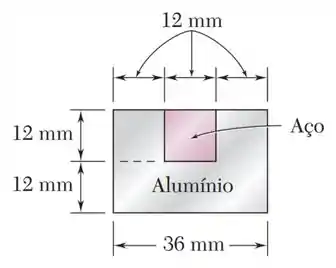
Um tubo de aço é responsável por fazer o transporte de petróleo e outros matérias líquidos em uma determinada região. Para reforça-lo foram usadas barras de alumínio como as mostradas na figura. Sabendo que essa seção foi submetida a um esforço fletor de módulo ,determine o valor da tensão máxima normal que ocorrerá na viga composta.
Questão 7
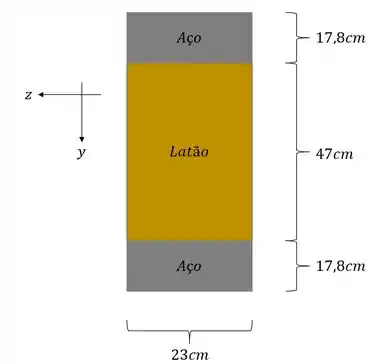
Deseja-se reforçar uma barra de latão usando duas barras de aço como mostradas na figura. Sabendo disso determine o valor da tensão normal máxima sofrida por essa peça que sofre a ação de um momento fletor de intensidade .
Questão 8
Calcule o valor da tensão normal no ponto A indicado da viga composta.