Massa e aceleração
Produzido por Pablo RicardoTeoria
Vamos, enfim, começar a conectar os dois grandes assuntos que estávamos estudando: As forças e os movimentos.
Agora pense na tirinha abaixo:

A Mônica exerceu uma força nos outros personagens e, por isso, eles se movimentaram. O que aconteceu?
A força exercida gerou uma aceleração. Vamos entender isso melhor?(:
2° Lei de Newton
O enunciado da segunda Lei de Newton é:
“Lei II: A mudança de movimento é proporcional à força motora imprimida, e é produzida na direção de linha reta na qual aquela força é aplicada.”
A mudança de movimento é expressa pela aceleração. Já a proporção com a força é assegurada pela massa.
Matematicamente falando:
Ou vetorialmente:
Bom, até agora fizemos uma revisãozinha de coisas que talvez você já tenha visto. Agora, vamos relembrar mais algumas coisinhas que você vai precisar pra fazer os exercícios:
Tópicos especiais
- Corpos conectados
- Plano inclinado
- Atrito
Uma primeira coisa importante a se falar é sobre corpos que se movem conectados. Por exemplo: corpos conectados por uma corda:
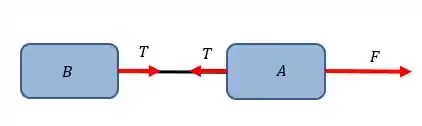
Como e estão presos um ao outro, podemos dizer que:
E:
O que isso significa? Significa que, para efeitos de cálculo, podemos dizer que são um corpo só. Assim, podemos calcular a aceleração do conjunto da seguinte forma:
E:
Devemos relembrar as coordenadas no plano inclinado. Para uma caixinha em um plano inclinado, possuindo um peso
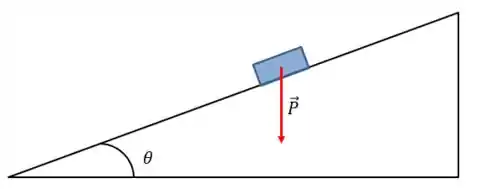
Podemos decompor a força peso em uma componente ao longo do plano inclinado e uma componente perpendicular a esse:
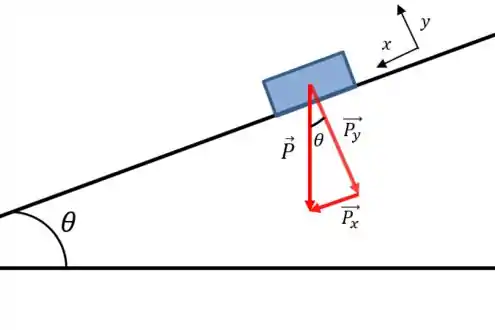
Onde:
Show de bola?
Temos dois casos: O atrito estático e o atrito cinético. A força de atrito estático máxima é dada por:
Caso um corpo esteja sofrendo a ação de uma força , o corpo passará a se mover e o atrito passará a ser cinético. A força de atrito cinético é dada por:
Nesse caso, a resultante das forças é dada por:
E é isso. Foi apenas uma pequena revisão. Vamos fazer exercícios agora (:
2° Lei de Newton
Tópicos especiais
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 94, 3/1
Durante um teste de frenagem, o carro com motor traseiro é parado a partir de uma velocidade inicial de em uma distância de . Se é sabido que todas as quatro rodas contribuem igualmente para a força de frenagem, determine a força de frenagem em cada roda. Suponha uma desaceleração constante para o carro de .

Passo 1
O sistema do problema pode ser representado por:
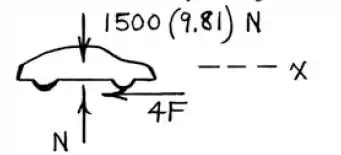
Passo 2
Para calcular a aceleração do carro, basta a gente usar Torriceli:
Só que
E precisamos converter
Além disso:
Assim:
Passo 3
Sabemos que as quatro forças são responsáveis pela aceleração:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 94, 3/5
O caminhão de puxa o reboque de . Se o conjunto parte do repouso em uma estrada horizontal com uma força de tração de entre as rodas do caminhão e a estrada, calcule a tração na barra de engate horizontal e a aceleração do veículo.
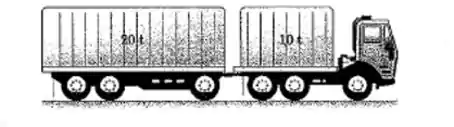
Passo 1
O sistema pode ser representado por:
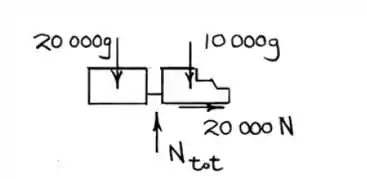
Podemos começar calculando a aceleração do conjunto como um todo:
O que fizemos? Como há um link entre os corpos, podemos considera-lo como um corpo só. Assim:
Passo 2
Para achar a tensão, basta considerarmos apenas o corpo traseiro separadamente:
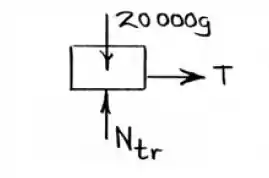
Sendo que esse corpo possui a mesma aceleração do conjunto, assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 95, 3/7
Calcule a aceleração vertical do cilindro de para cada um dos dois casos ilustrados. Despreze o atrito e a massa das polias.
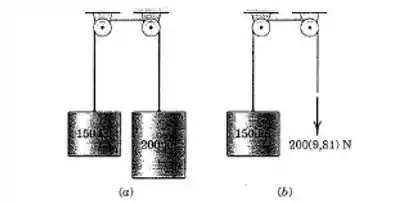
Passo 1
a)
Podemos representar o sistema assim:
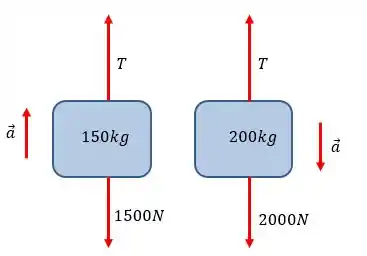
Do primeiro corpo:
Do segundo:
Somando:
Passo 2
b)
Nesse caso, o sistema pode ser representado por:
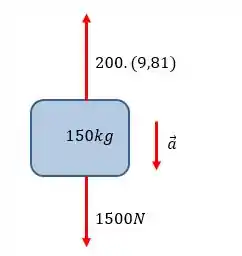
Assim:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 94, 3/2
O caixote de está parado quando a força é aplicada. Determine a aceleração resultante do caixote se , e .
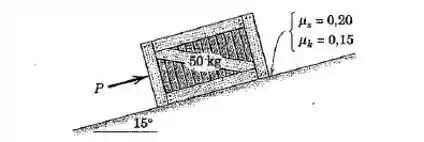
Passo 1
O sistema da figura vamos pode ser descrito por:
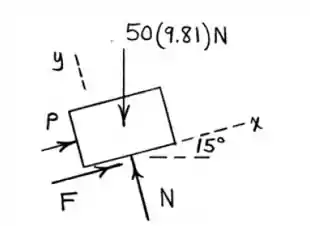
Temos a força , a força de atrito , a força normal e o peso .
Passo 2
a)
Para , vamos ter o seguinte equilíbrio no eixo perpendicular ao plano:
E a resultante na direção vale quanto? Vamos, primeiro, calcular o módulo da força de atrito estática máxima:
E quanto vale a componente do peso? Vale
Como podemos ver, a força peso na direção do plano inclinado tem valor maior do que . Assim, ocorrerá deslizamento e o atrito atuante será cinético:
Passo 3
b)
O equilíbrio vertical continuará o mesmo, já que atua na direção do plano:
Agora vamos analisar a força resultante na direção do plano:
Lembra da força de atrito máxima? Vale:
Como:
A força não consegue vencer a força de atrito: Não há deslocamento:
Passo 4
c)
Vamos fazer a mesma coisa:
E:
Como:
Vai haver movimento, dado por:
Resposta
a)
b)
c)
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 97, 3/23
Se os coeficientes de atrito estático e dinâmico entre o bloco de e o carrinho de têm ambos essencialemente o mesmo valor de , determine a aceleração de cada parte para e .
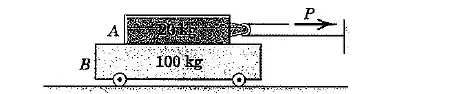
Passo 1
a)
Vamos primeiro analisar o bloco Temos duas forças atuando nesse corpo:
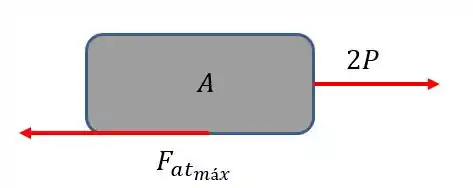
Por que vale Porque existe uma roldana, o que duplica a força.
E quanto vale
Basta usarmos:
Onde é o módulo da força normal que exerce em . Essa força, no caso, é o peso de
Assim:
E assim:
Perceba que:
Passo 2
Vamos assumir que ocorre deslizamento: que tem uma aceleração diferente de e que, por isso, se desloca sobre . Nesse caso, não podemos considerar os dois corpos como um só. Assim:
Vamos calcular a aceleração de
Agora vamos calcular a aceleração de
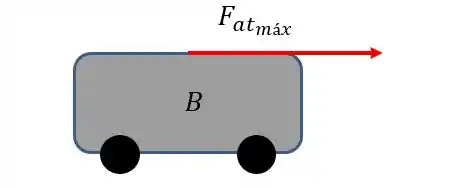
só sofre a ação da força , já que não possui atrito com o solo( já que possui rodinhas). Assim:
Agora veja:
Ou seja, o bloco se desloca em cima de
Passo 3
b)
Nesse caso, o continua sendo o mesmo. No entanto:
Sendo assim, como a força não é suficiente para vencer a força de atrito, não ocorre o deslizamento. Isso quer dizer que podemos tratar o conjunto dos dois corpos como um só:
Assim:
Resposta
a)
b)
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 94, 3/6
Um esquiador parte do repouso sobre uma encosta com no instante de tempo e registra o tempo quando passa um ponto de coeficiente de atrito dinâmico entre a neve e os esquis. Percorrendo 20m a partir daí. Despreze a resistência do vento. Encontre o coeficiente de atrito dinâmico entre a neve e os esquis.
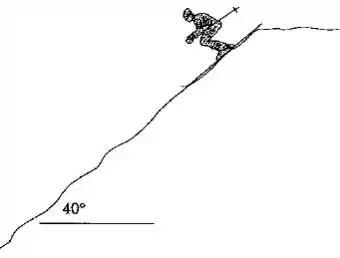
Passo 1
Beleza, quais são as forças que agem no esquiador? A força peso e a força de atrito. Podemos esquematizar o sistema assim:
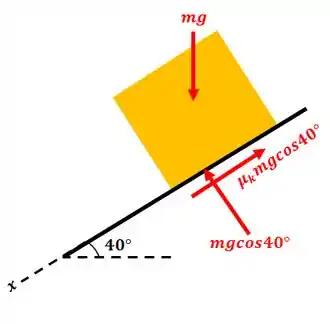
Passo 2
Vamos calcular a aceleração do homem:
Passo 3
Para uma aceleração constante, no entanto, temos:
Como ele parte do repouso, a sua velocidade inicial é ...
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Dinâmica, 6° ed. RJ: LTC, 2009, 96, 3/17
A esfera de aço está suspensa na estrutura acelerada pelas duas cordas e . Determine a aceleração da estrutura que fará com que a tração em seja o dobro daquela em .
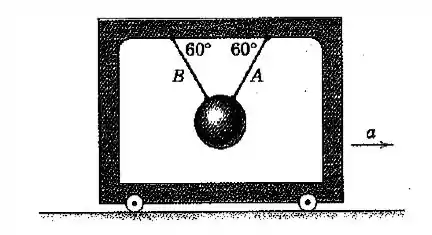
Passo 1
Podemos representar o sistema assim:
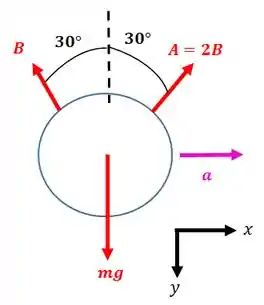
Decompondo na direção e fazendo o equilíbrio:
Passo 2
Decompondo as forças na direção e fazendo o equilíbrio, temos que:
Assim, jogando na primeira equação: