Corpos Compostos
Produzido por Pablo RicardoTeoria
Introdução
Você já aprendeu a calcular o centróide de áreas, volumes ou massa de algumas figuras.
Mas as figuras eram simples. Concordo que não eram necessariamente fáceis, mas não tinha nenhum corpo mirabolante.
Agora lhe apresento com o que lidaremos neste tópico:
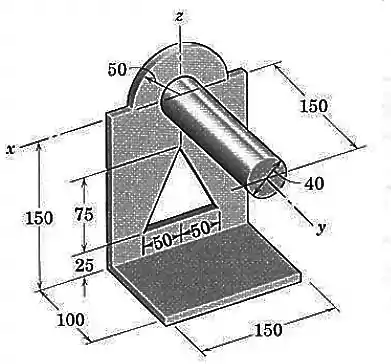
Perceba que esta figura é composta de várias formas geométricas conhecidas: tem um cilindro, um retângulo, uma metade de circunferência, um buraco em forma de triângulo...
Agora vamos aprender a lidar com isso aí! Partiu?
Calculando os centros de corpos compostos
Quando você se deparar com um corpo formado por várias figuras geométricas conhecidas (ele é chamado de corpo composto) podemos ser dividido-lo em suas partes conhecidas e achar o centróide de cada um delas.
Para calcular as coordenadas do centróide de um corpo composto, basta a gente usar os somatórios abaixo:
O que está dentro do somatório é a coordenada do centróide de cada parte que compõem o corpo e o representa a área dessas figuras conhecidas.
Também tem as coordenadas e :
Essas fórmulas acima são para o centróide de áreas, mas se você quiser achar o centróide para volumes e linhas é só trocar o por de volume ou de comprimento!
Corpos com Furos
Se o corpo apresentar um furo e esse furo tiver um formato conhecido como este do exemplo abaixo que tem uma forma de triângulo:
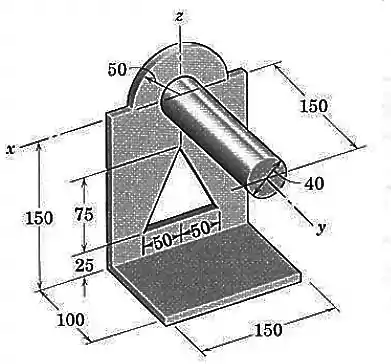
Devemos tratar a área do triângulo como negativa, pois ueremos retirá-la da nossa área total. Então, se a área vale , nós colocamos no somatório !
Exemplo
Para fazer os cálculos, facilita muito fazer esta tabela aqui:
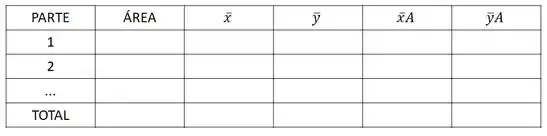
Não esqueça de colocar tudo na mesma unidade.
Vamos calcular a coordenada do centroide desta figura aqui:
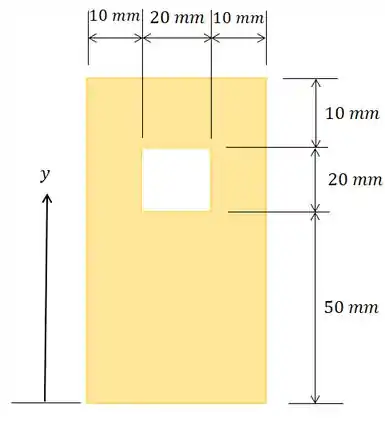
Primeira passo que temos que fazer é identificar as figuras conhecidas e nomeá-las:
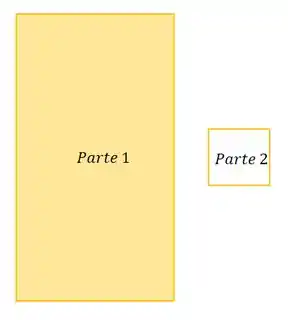
Segundo passo é calcular a área de cada parte:
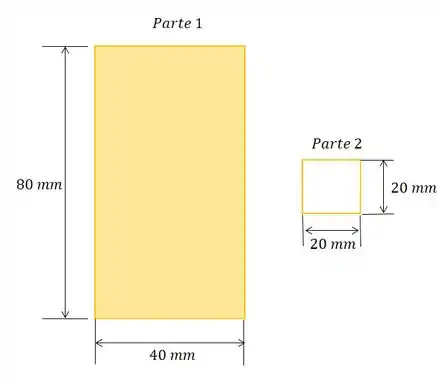
Mas não esqueça que a é um furo, logo sua área deve ser negativa. Então, a nossa tabela fica assim:
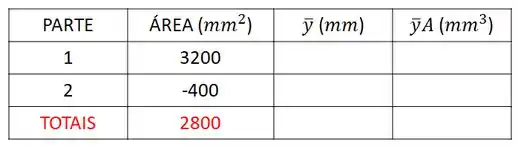
Repare que como não estamos calculando a coordenada , foram tiradas duas colunas da tabela.
Terceiro passo é identificar as coordenadas da cada uma das partes que forma a figura e ir completanto a tabela:
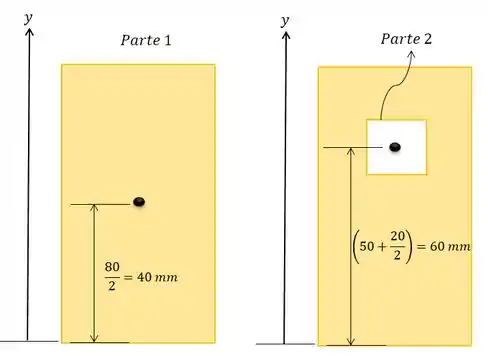
Repare que o centróide do retângulo fica no seu centro geométrico, ou seja, na metade da sua altura. Então, vamos completar a nossa tabela com a coordenada de cada parte:
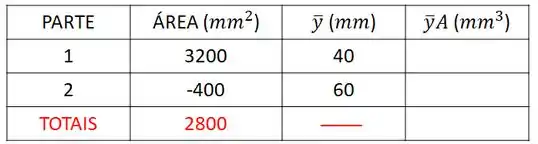
Quarto passo é multiplicar a área de cada parte por sua respectiva coordenada :
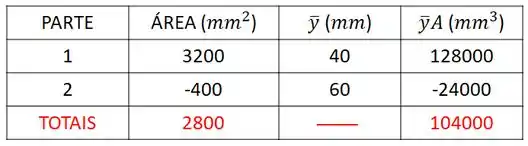
Quinto passo é só aplicar a fórmula agora:
Sabendo que:
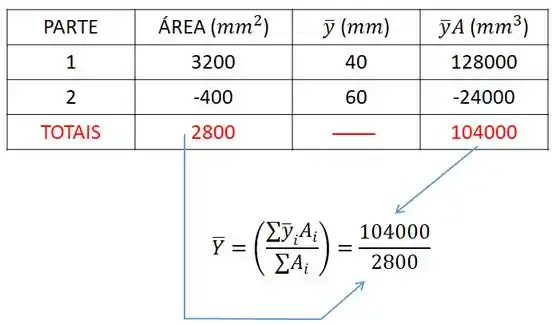
Então:
DICA: se uma figura for simétrica, o centroide sempre vai estar em cima do eixo de simetria da figura!
Então, é isso que vamos fazer nos exercícios!
Bora praticar! ![]()