Centros e Centróides
Teoria
Introdução
Na maioria das questões de mecânica você tem uma estrutura e precisa saber onde posicionar a força peso, não é mesmo?
Se você tem uma figura geométrica simétrica e homogênea, como um quadrado, você sabe que tem que colocar a força peso no seu centro geométrico:
E se você tem uma figura diferente como esta aqui:
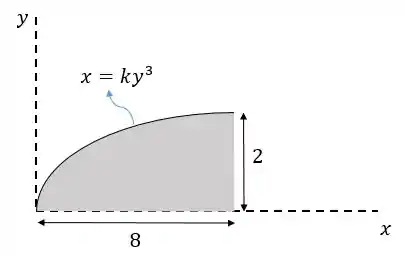
Onde posicionar a força peso?
É isso é o que vamos aprender nesse tópico: como calcular centros de corpos e até mesmo
Partiu?
Centro de gravidade
Centro de gravidade é o local onde o peso de um corpo está uniformemente distribuído. Por exemplo, no corpo humano o centro de gravidade é mais ou menos no umbigo!
Show de bola! Mas na mecânica o conceito de centro de gravidade não é tão utilizado assim. Nós vamos falar mais sobre centro de massa e centroide (que é o centro geométrico).
Por que disso?
O centro de gravidade leva em conta o campo gravitacional, enquanto o centro de massa leva em conta apenas a distribuição da massa pelo corpo. Como em 99,9999% dos problemas de mecânica envolvem campos gravitacionais uniformes, então o centro de massa e centro de gravidade coincidem.
Centro de massa
Na mecânica é muito importante saber o centro de massa de algumas figuras como: o retângulo, o triângulo e o círculo. Além disso, é importante saber calcular esse centro para outros formatos, como o nosso problema em questão:
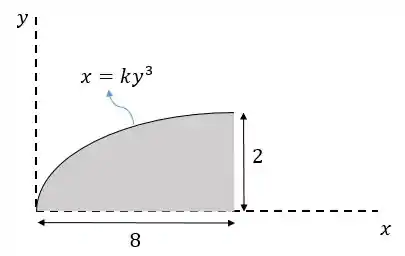
Antes de fazermos esse problema, vamos focar em situações mais corriqueiras e menos complexas, como o retângulo e o triângulo.
Centroide
Quando falamos de figuras geométricas a gente também não precisa ficar pensando em termos de massa, porque normalmente a massa está distribuída uniformemente pelo corpo. Dessa forma, o centroide (que é o centro geométrico, ou baricentro) é o próprio centro de massa, que é o próprio centro de gravidade (no caso de campo gravitacional uniforme).
Então na maioria esmagadora das vezes nós podemos pensar da seguinte forma:
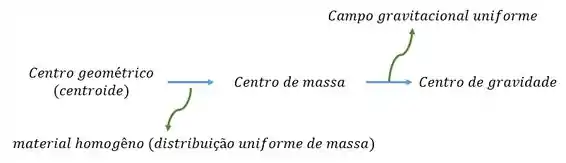
- Centro de massa de um retângulo.
- Já no caso de um triângulo nós vamos ter que o centroide está localizado no encontro das alturas. Perceba que o importante aqui é lembrar da relação .
Se nós tivermos um retângulo seu centroide estará localizado exatamente no meio da altura e da base:
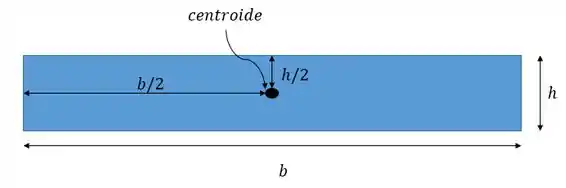
Acredito que não tenha nenhum mistério até aqui.
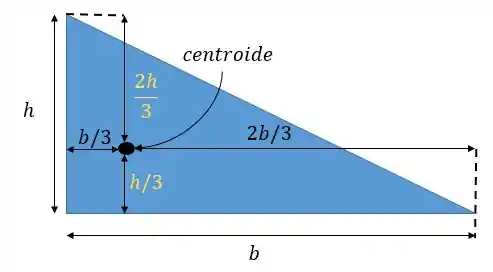
Esses dois centroides são os mais utilizados com certeza. Mas agora acho que já da para resolver o nosso problema inicial vocês não acham?
Resolvendo com integral
Vamos olhar novamente o nosso probleminha:
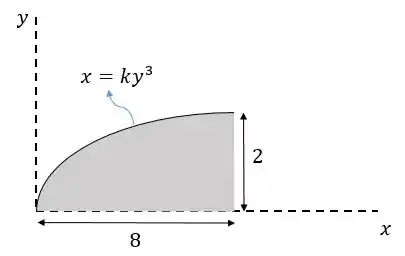
Temos de achar o centro de massa desse corpo (ou centroide, ou centro de gravidade. Como temos uma figura homogênea e um campo gravitacional uniforme então fica tudo no mesmo local).
Talvez vocês se lembrem que é possível calcular o centro de massa de um sistema com de partículas da seguinte forma:
Quando a gente transforma isso em integral vamos ter:
Mas como a gente tá falando de uma figura geométrica e nem temos a massa, então vamos colocar em função da área:
E temos também a coordenada do centro de massa:
Onde cada termo e é o centroide de cada retângulinho infinitesimal. Olha só:
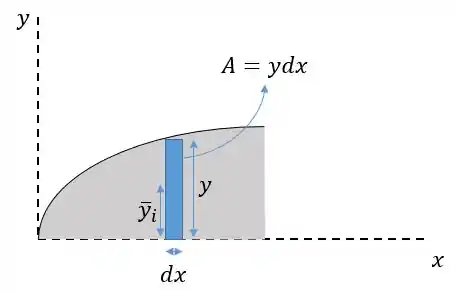
Com esse retângulo vertical a gente pode achar a coordenada vertical do nosso centroide, mas é importante saber a área. Então vamos calcular a área cinza primeiro:
Faz sentido né? o variando de até , agora só falta achar uma equação para . Se
Então:
Logo,
Pessoal, vamos achar o valor de para ficar mais fácil. No ponto o valor de é: . Portanto:
Substituindo na nossa equação:
Resolvendo:
Agora vamos calcular o ponto do centroide:
Substituindo o que já temos:
Aí aqui é importante prestar ATENÇÃO. é a própria altura do retângulo infinitesimal, só vamos transformar de para para resolver a equação. Já é o centroide do retângulo infinitesimal. Sendo assim,
Fazendo a substituição que já havíamos feito antes:
Então nossa integral será da forma:
Reorganizando:
Resolvendo, lembrando que os limites continuam sendo de a :
Então no nosso desenho o centro de massa vai ficar em algum ponto em cima da linha vermelha:
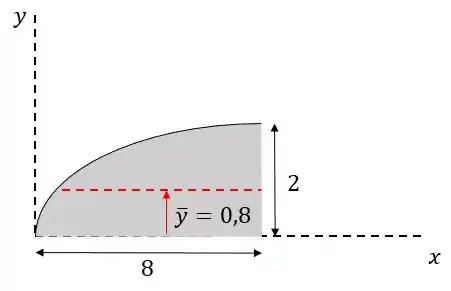
Repare que sabemos apenas a altura, não sabemos a posição . Para isso vamos fazer de forma análoga o cálculo da integral para dessa vez utilizando barrinhas horizontais:
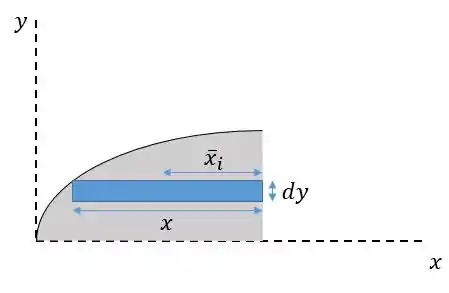
Agora o termo de área é dado por:
Perceba que invertemos né? É legal perceber que não precisamos calcular a área toda novamente. Então a nossa equação vai ficar da forma:
O termo depende de da seguinte forma (aqui já vamos considerar ):
Mas e o termos ? Ele vai ser metade de :
Substituindo na equação:
Reorganizando e lembrando que a integral agora vai de até temos:
Resolvendo:
Maaaass tem um detalhe, esse valor de é quando medimos o centroide a partir do ponto então a localização do centroide é:
Prontinho!!! Achamos o nosso ponto exato do centro de massa:
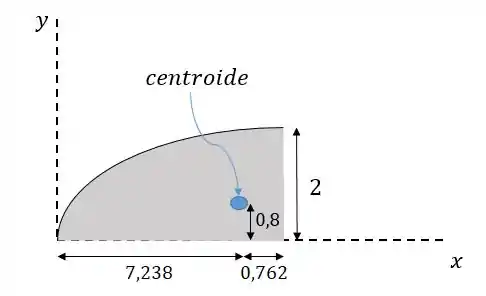
Pessoal, só pra finalizar essa parte vou deixar uma tabelinha aqui com outras integrais úteis.
Outros tipos de centros
Centro de massa
Centroide
Resolvendo com integral
Outros tipos de centros
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 184, 5/6
Determine as coordenadas do centróide da área sombreada.
Passo 1
Legal, o nosso primeiro passo é descobrir quem é
Para isso, perceba que para temos , então vamos pegar a equação da curva e substituir isso nela:
Assim, a equação da curva pode ser escrita assim:
Passo 2
Agora vamos calcular a área da região sombreada, vamos calcular a área a partir de retângulos horizontais infinitesimais, que tem a base igual a e altura igual a , como mostrado:
Observe que a área de cada retângulo é dada por:
Dessa forma vamos ter a área da figura como a integral desses retângulos:
Sabendo que é:
Vamos substituir isso dentro da nossa integral e resolver sabendo que varia de zero até :
Agora que temos a área vamos achar os centroides, lembrando que temos de achar o centroide para ambos os eixos e isso pode ser feito através das seguintes equações:
Passo 3
Agora vamos achar o Para isso, usamos:
O dentro desta integral indica a distância horizontal de cada retângulo infinitesimal que criamos até o nosso eixo, assim:
Isso porque sabemos que o centróide de um retângulo fica na metade do seu comprimento. Então, vamos ter que:
E ficamos então com:
Vamos resolver só a parte de cima da equação, para não ficar confuso:
Lembrando que , então:
Pronto, achamos a parte de cima da nossa equação:
Passo 4
Agora vamos calcular :
O é a distância vertical de cada retângulo infinitesimal até o eixo horizontal.
Sabendo que e , temos que:
Vamos novamente resolver só a parte de cima da equação e sabendo que varia de zero até , temos:
Pronto, agora podemos achar sabendo que já calculamos a área desta figura no :
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 184, 5/7
Determine a coordenada do centróide da área sob a curva senoidal mostrada.
Dica:
Passo 1
Vamos usar aqui novamente a nossa relação:
Passo 2
Nós podemos começar calculando a área
Mas quem é vale:
Mas sabemos a equação da curva:
Substituindo isso na equação de , temos que:
Então, sabendo que varia de zero até , a área fica:
Aplicando os limites até
Passo 3
Agora vamos calcular a parte de cima da equação de :
Perceba que , nesse caso, se refere à distância vertical do centroide de cada retângulo que criamos até o eixo horizontal.
Então:
Lembrando que , então podemos escrever:
O intervalo de integração de vai de zero até , então:
Aplicando a dica que foi dada no enunciado da questão:
Aqui eu usei a fórmula:
Assim:
Passo 4
Por fim, só aplicar:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 184, 5/29
Localize o centróide da área sombreada entre as duas curvas.
Passo 1
Em primeiro lugar, vamos escrever ambas as equações em função de . A primeira já está:
E a segunda equação fica assim:
Show de bola?
Passo 2
Agora vamos calcular a área da figura:
Perceba que a área vai ser o somatório tendendo ao infinito, ou seja, uma integral, dos pequenos retângulos. A área de cada retângulo, por sua vez, é dada por:
Mas o limite superior do retângulo é dado pela equação e o limite inferior pela equação , então podemos escrever que é a diferença entre as funções:
Como varia de zero até , podemos dizer que a área é:
Assim:
Agora podemos usar as duas relações abaixo:
Passo 3
Vamos então calcular primeiro .
O dessa equação, no caso, é o próprio já que a distância de cada retângulo infinitesimal até a origem é justamente
Lembrando que , então:
Resolvendo isso, temos que:
Passo 4
Agora vamos calcular :
Como estamos lidando agora com a componente vertical, cada vai ser a média das funções:
Assim:
E sabemos que , então:
Lembra disso aqui:
Vamos usar isso para os termos dentro da integral:
Ficamos com isso aqui:
Passo 5
Pronto! Agora é só aplicar:
E:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 188, 5/35
Calcule a distância medida desde a base até o centróide do volume do cone truncado.
Passo 1
Vamos desenhar um esquema do cone:
Repare que a orientação de aponta para baixo.
Depois voltaremos para ele. Vamos agora calcular o volume.
Para isso vamos criar um círculo de raio e espessura infinitesimal :
Agora, para se calcular , temos que escrever uma função em função de .
Passo 2
Note que o contorno do cone é uma reta. Vamos girar a figura para facilitar a visualização:
Perceba que cresce conforme cresce, sendo o , e o
Assim, sendo:
Para , temos que
E quando , temos que
Assim:
Passo 3
Show de bola. Agora podemos calcular o volume, sabendo que e que:
Obs: Perceba que o limite inferior é pois se trata de um tronco de cone que começa em e termina em .
Resolvendo esta integral, temos que:
Aplicando os limites:
Passo 4
Para calcular , temos que aplicar:
Temos que calcular , sabendo que e que, então:
Passo 5
Assim:
E como ele tá pedindo a altura da base até o centroide:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 188, 5/22
Determine a coordenada do centroide da área sombreada.
Passo 1
Vamos começar definindo as funções:
Para temos que, então:
Substituindo o valor de na equação da curva, vamos ter que:
Isolando , vamos ter que:
A outra função é uma reta:
Para temos que , então:
Para temos que , então:
Então ficamos com:
Passo 2
A área será dada por:
Repare que o elemento é dada pela diferença entre as duas funções, assim:
Então:
Passo 3
Agora vamos calcular a coordenada de :
Como já calculamos a área, vamos calcular agora o termo :
Pra calcular o que aparece dentro da integral, temos que usar sempre o , que é a média entre as funções:
Sabendo que , temos que:
Resolvendo esta integral, temos::
Então, a coordenada é:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 188, 5/205
Determine as coordenadas e do centróide da área sombreada.
Passo 1
Estamos procurando as coordenadas eda área da figura. Uma das equações nós sabemos:
Quanto vale ? Sabemos que quando o valor de também é , então vamos substituir isso na nossa equação:
Dessa maneira, ficamos com esta equação aqui:
Mas e a equação da reta? Vamos ter que descobrir... Sabemos que uma equação da reta genérica tem a seguinte equação:
E que quando temos que , então vamos substituir isso na nossa equação genérica:
E perceba também que quando temos que , vamos substituir isso novamente na nossa equação genérica:
Agora temos um sistema:
Como sabemos que , vamos substituir isso na primeira equação do sistema:
E vai valer:
Então, a equação da reta fica:
Passo 2
Para achar o , vamos usar as equações em função de já que assim vai ficar mais fácil:
E:
Vamos criar retângulos para fazer a integração de modo que será:
Passo 3
Vamos começar calculando a área da região sombreada. A área que está entre as duas curvas acima vai ser dada por:
Sabendo que varia de até , vamos ter que:
Podemos dividir isso em três integrais para facilitar a resolução:
Passo 4
Agora vamos resolver o termo de cima na nossa equação de :
O dentro da integral é a distância do centróide de cada retângulo até o eixo horizontal:
Sabendo que:
Então, será:
Separando em três integrais, vamos ter que:
Então, a nossa coordenada será:
Passo 5
Vamos calcular agora a coordenada . Para isso, vamos calcular o termo de cima da fórmula:
O dentro da integral é a distância do centróide do retângulo que criamos para integrar até o eixo vertical. Essa distância é a média entre as duas funções, assim:
Vamos ter que será:
Sabendo que continua o mesmo:
Então:
Repare que usamos a propriedade que diz que:
Substituindo as funções de e , temos que:
Agora sim podemos calcular a coordenada :
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 188, 5/36
Determine a coordenada do centro de massa da casca esférica, que tem espessura uniforme, mas fina.
Passo 1
Podemos representar a esfera por uma imagem bidimensional da mesma:
Perceba que, para uma pequena variação , existe uma pequena área superficial relacionada.
Agora vamos começar a pensar em termos de massa: uma quantidade infinitesimal de massa será dada por:
Perceba que é a espessura da “fatia” infinitesimal da esfera e que é a circunferência.
Opa, mas veja só isso: de acordo com o nosso desenho, podemos escrever: , né?
Então:
Show de bola, agora já sabemos que temos que integrar isso daí pra conseguirmos a massa.
Passo 2
Beleza, vamos integra isso em
Mas qual é o intervalo de integração? Bom, o ângulo varia desde zero até o ângulo final que gera aquele espacinho de
Esse ângulo final pode ser calculado pela tangente do triângulo final formado:
Quanto vale o cosseno desse ângulo?
Assim:
Show?
Agora já podemos aplicar:
Passo 3
Analogamente ao que fizemos com , podemos escrever na forma:
Então:
Lembrando que:
Podemos escrever:
Integrando:
Passo 4
Aplicando a nossa equação de :
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 188, 5/211
O corpo afilado tem uma seção transversal horizontal circular. Determine a altura de seu centro de massa, acima da base do sólido homogêneo.
Passo 1
Neste exercício queremos achar o centro de massa, então vamos usar essa fórmula aqui:
Para isso, temos que definir o que será o nosso . Mas para isso você precisa lembrar que o cálculo da massa de um corpo que tem uma massa específica é:
Onde é o volume do corpo. Se derivarmos ambos os lados dessa equação, vamos ter que:
Então, o que precisamos definir na nossa figura é um elemento de volume . Para isso, vamos criar cilindros de espessura infinitesimal. Vendo de frente nossa figura fica assim:
Repare que é a equação da reta que limita o lado direito da nossa figura.
Mas estamos criando cilindros de espessura bem pequena, assim:
Então, o volume deste cilindro fica assim:
Onde é a altura e é o raio. Mas como temos uma espessura bem pequena, nosso volume será bem pequeno também:
Agora vamos substituir na nossa equação de :
Elevando o termo de dentro dos parênteses ao quadrado, temos:
Passo 2
Nosso próximo passo é achar a equação da reta que limita o lado direito da nossa figura. Para isso, sabemos que uma equação da reta genérica tem o seguinte formato:
E quando temos que , então a nossa equação fica:
E quando temos que e agora a nossa equação fica:
Então, a equação da reta fica:
Passo 3
Agora vamos substituir a equação da reta que acabamos de achar na nossa equação de :
Vamos colocar para fora dos parênteses:
Passo 4
Agora vamos achar a massa do nosso corpo e para isso temos que resolver a integral:
Como é constante vamos passá-lo para fora da integral. E sabemos que varia de até , então:
Vamos dividir isso e três integrais para facilitar:
Resolvendo estas integrais, temos que:
Passo 5
Agora vamos achar o termo de cima na nossa equação:
Repare que o de dentro da integral é a distância do centroide do cilindro que criamos até o eixo horizontal:
Ou seja, vamos calcular :
Vamos passar o termo que é constante para fora da integral:
Vamos separar em três integrais sabendo que varia de até :
Passo 6
Pronto, agora é só substituirmos na fórmula para achar a coordenada de :
Então, a altura do centro de massa do sólido é: