Teorema de Pappus
Produzido por Pablo RicardoTeoria
E aí, seja bem vindo ao Responde Aí!
Os teoremas de Pappus (ou Teoremas de Papo) nos ajudam a achar a área e o volume dos sólidos de revolução.
Quer entender melhor de onde vieram essa fórmulas, e aprender como usar os Teoremas de Pappus? Então é só ficar aqui nessa aula com a gente!
Sólidos de revolução
Existem certos corpos que podem ser obtidos pela rotação de uma figura em torno de um eixo. Esse é o caso de um toróide:

Se olharmos uma seção do toróide vemos um círculo, não é mesmo?
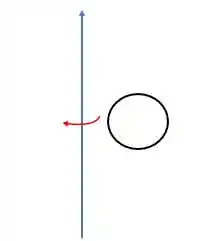
Perceba que se girarmos esse círculo em torno do eixo
Mas como a gente calcula a área de superfície e o volume desse toroide? Imagina só o trabalhão que deve ser aplicar uma integral nisso daí?!
Mas graças aos Teoremas de Pappus, a gente pode calcular a geometria de sólidos de revolução com facilidade.
Teorema de Pappus para a área superficial
Para achar a área superficial de um corpo que seja gerado através da rotação de uma figura em relação a um eixo que não intercepte esta figura, iremos usar esta fórmula aqui:
Onde:
- O
é a distância do centroide da figura que vai girar até o eixo em torno do qual ela está girando; - O
é o perímetro, ou contorno, da figura vai girar.
Se estivéssemos calculando a área da superfície do toroide, o
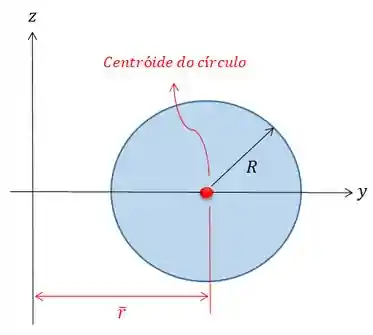
E como
Beleza?
Então, lembre-se: você sempre vai calcular primeiro o centróide da figura, por meio dos métodos que já vimos, e depois calcular o seu perímetro.
Teorema de Pappus para o Volume
Se quisermos calcular o volume, vamos usar esta fórmula aqui:
Onde
- O
continua sendo a distância do centróide da figura até o eixo em torno do qual a figura gira. - O
é a área da região que vai gerar o sólido.
No nosso exemplo do toróide, o seria a área do círculo que ao girar em torno do eixo forma o sólido:
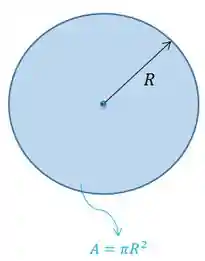
Teoremas de Pappus: Caso Geral
E se quisermos gerar um corpo rodando-o apenas
Claro que sim! Nesse caso, usamos as fórmulas:
O
Viu só! Os Teoremas de Pappus são fáceis de aplicar e super úteis!
Mas pra garantir aquele 10, que tal ver um vídeo sobre o Teorema de Pappus?!