Teoria
Introdução
Imagine que você queira puxar uma caixa bem pesada pelo chão:

Inicialmente é necessário fazer uma força bem grande para esta caixa se mover, não é mesmo?
Por que temos que fazer tanta força para tirar a caixa da inércia? Isso ocorre porque existe uma força que é contrária ao movimento chamada atrito.
Nesse tópico vamos aprender sobre dois tipos de atrito: o atrito estático e o atrito dinâmico.
Partiu?
Atrito Estático
O atrito estático é aquela força contrária ao movimento que surge antes do corpo entrar em movimento, daí o seu nome ser atrito estático.
Este tipo de atrito pode variar de zero até o máximo valor antes do corpo entrar em movimento, ou seja, quando o corpo está na iminência de se movimentar.
Nas questões de atrito o que precisamos saber é a força máxima () que se pode aplicar antes do corpo entrar em movimento e para isso vamos usar esta fórmula aqui:
Onde:
- é o coeficiente de atrito estático e isso geralmente é dado no enunciado;
- é a força normal, ou seja, aquela força que surge sempre que há contato do corpo com a superfície de apoio.
Atrito Dinâmico
O atrito dinâmico () é aquele atrito que surge após o corpo entrar em movimento, daí o seu nome ser atrito dinâmico.
Para calcular o seu valor, que agora vai ser constante, vamos utilizar esta fórmula aqui:
Onde:
- é o coeficiente de atrito dinâmico e geralmente é dado no enunciado;
- é a força normal devido ao contato do corpo com a sua superfície de apoio.
Atrito Estático versus Atrito Dinâmico
Já reparou que é preciso muito mais força para colocar um corpo em movimento do que para manter o seu movimento? Isso ocorre porque a força de atrito dinâmico é menor do que a força de atrito estático.
Podemos visualizar isto neste gráfico:
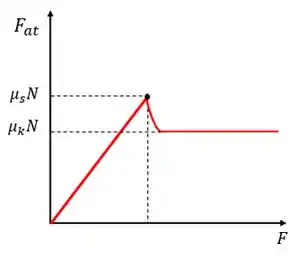
No eixo horizontal temos uma força que é aplicada no corpo e no eixo vertical temos a força de atrito que surge como consequência disso.
Ao aumentarmos a força aplicada, aumentamos a força de atrito até que ela atinge um máximo () depois o atrito diminui até o patamar do atrito dinâmico () e fica constante.
Observação: existe uma breve região de transição entre o atrito estático e o dinâmico, mas nos exercícios você pode desconsiderá-la. Então, se o atrito for maior que o estático, considere-o como atrito dinâmico e pronto.
É estático ou é dinâmico?
Voltando ao nosso bloquinho... E se um problema te der uma força e te pedir para calcular o valor da força de atrito?
Vamos dizer que os seguintes dados são mencionados: , e .
Quando aplicamos uma força puxando o bloquinho surge uma outra força contrária ao movimento que é a força de atrito :
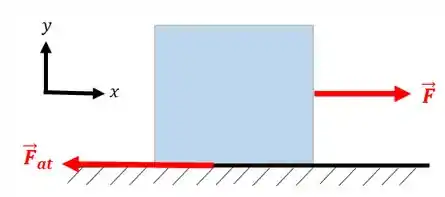
Neste tipo de problema vamos admitir inicialmente que o atrito é estático, ou seja, o corpo está parado. Então, vamos fazer o equilíbrio de forças:
Observação: nós também admitimos um sentido para o atrito. Caso o resultado da etapa acima der negativo, inverta o sentido da força de atrito e tudo certo!
Agora vem o teste: será que a força de atrito está realmente na região estática? Para saber isso você precisa calcular a força de atrito máxima.
Mas antes é necessário saber a força normal . Podemos fazer isso usando o equilíbrio vertical:
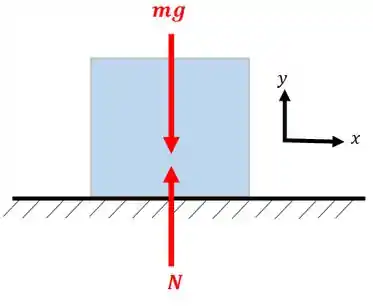
Sabendo que o peso do bloquinho é:
Então:
Pronto, agora podemos calcular a força de atrito estático máxima:
Opa, nesse caso:
já que
Então, realmente o corpo está parado e o atrito estático tem valor igual a:
Show de bola?
Agora vamos aumentar um pouco a força para ver o que acontece... Vamos fazer :
Nesse caso:
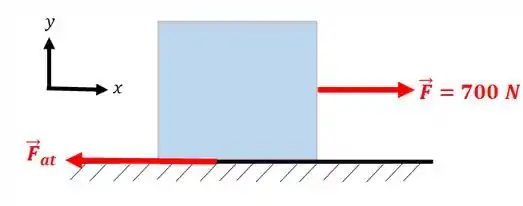
De novo vamos partir do princípio que o atrito é estático e que o corpo está parado:
Como o peso do bloquinho não mudou, o seu peso continua o mesmo. Desse modo, a força de atrito estático máxima também não muda:
Mas desta vez a força que aplicamos gerou um atrito maior que o atrito estático máximo:
já que
Então, o atrito na verdade é dinâmico e não estático como supomos inicialmente.
E como se calcula o atrito dinâmico? É só usarmos a nossa equação:
Ou seja, neste último caso que fizemos o atrito é dinâmico, pois o corpo vai estar em movimento e seu valor é:
Sacou?
Vamos fazer uns exercícios pra entendermos melhor!