Energia Potencial
Teoria
Introdução
Você já ouviu falar que energia nunca pode ser destruída? Isso porque ela só pode ser transformada ou transferida...
Vamos supor que você ame esporte radical e vá praticar bungee jump!
Quando você está laaaá em cima, você tem uma energia que é associada a sua altura. E quando você começa a descer, a sua energia é transformada em movimento.
No caso do bungee jump, você é amarrado a uma corda elástica, então quando você estica totalmente a corda é como se você estivesse esticando um elástico. Dessa forma, esta corda faz um movimento de vai e vem até que a energia se dissipe totalmente!
Podemos dizer, então, que energia potencial é a capacidade que um corpo tem de realizar alguma ação.
Vamos aprender sobre a energia associada a uma altura e a energia associada a um corpo de propriedades elásticas. Então, bora começar!!!
Energia potencial: gravitacional e elástica
A energia potencial gravitacional está relacionada à altura que algum objeto que possui massa tem com relação a um referencial. Então, para que possamos medir alguma altura devemos primeiro atribuir um referencial nulo para alguma posição:
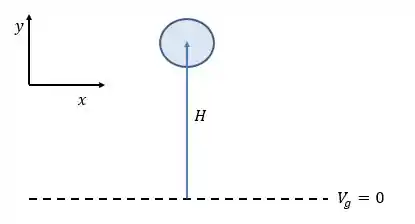
A altura é medida em relação a linha onde que é o nosso referencial. É importante perceber que também é preciso adotar um sentido para medição. Com o eixo apontado para cima, alturas acima de são positivas e alturas abaixo, negativas.
Bom, a fórmula geral para se calcular a energia potencial gravitacional é:
Onde é a distância do centro de gravidade do corpo até a linha em que .
No caso da energia potencial elástica (), devemos proceder da mesma forma: adotamos uma origem para que possamos calcular os deslocamentos de um certo corpo. Assim:
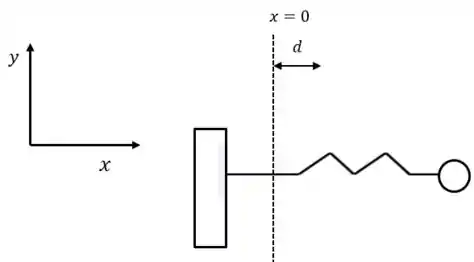
E a energia é dada por:
Observação: algumas vezes o enunciado vai te dizer que a mola já está esticada em ou . Nesse caso, vamos ter que:
Onde é o deslocamento inicial e é o deslocamento adicional que você vai calcular.
Equilíbrio
Para que um sistema esteja em equilíbrio temos que satisfazer as seguintes condições:
Ou:
Ou, de forma geral:
Onde é o que varia na função (pode ser um ângulo, um comprimento na horizontal, na vertical, etc)!!!
Então, por exemplo, se a função for igual a:
O que devemos fazer é derivar esta expressão com relação à variável da equação (neste caso é ):
E depois igualar o resultado a zero:
Então, essa será a posição de equilíbrio!
Tipos de estabilidade
Além de determinar o ponto de equilíbrio, esse método nos permite determinar qual é a condição de equilíbrio: se é um equilíbrio instável, estável ou indiferente.
Vamos primeiro falar um pouco sobre cada um deles:
- Equilíbrio instável:
- Equilíbrio estável:
- Equilíbrio Indiferente:
Um sistema está em equilíbrio instável quando existe o equilíbrio, porém, ao se aplicar qualquer força o sistema sai do equilíbrio. Podemos dar o exemplo da bolinha abaixo:
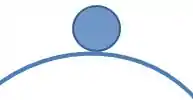
Nesse caso, o sistema não perde o equilíbrio por qualquer coisa. Se você aplicar uma força, o sistema tenderá a voltar ao equilíbrio, como no caso de uma bolinha em uma região funda:
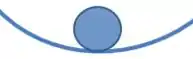
Nesse caso, se existir a ação de uma força em um sistema, ele nem terá uma tendência a retornar ao equilíbrio nem sair dele. É o caso, por exemplo, de uma bolinha em chão plano:
Para se determinar qual é o tipo de equilíbrio, basta a gente calcular a derivada segunda da função e substituir nesta expressão da segunda derivada o valor que achamos para a posição de equilíbrio no passo anterior.
Por fim é só verificar o sinal do resultado final que achamos seguindo estas condições aqui:
Então, nestes tipos de questões você deve:
- Adotar um referencial onde a energia potencial gravitacional será zero;
- Achar a equação da energia potencial total;
- Derivar a equação da energia potencial total e igualar a zero para achar a posição de equilíbrio;
- Derivar a equação da energia potencial mais uma vez e analisar se o resultado é igual, maior ou menor que zero para classificar o tipo de equilíbrio.
Partiu praticar?
Equilíbrio
Tipos de estabilidade
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 308, 7/35
A energia potencial de um sistema mecânico é dada por , onde é a coordenada de posição associada ao único grau de liberdade. Determine a posição, ou as posições, de equilíbrio e a condição de estabilidade do sistema de cada posição de equilíbrio.
Passo 1
Nosso primeiro passo é derivar com relação à a expressão da energia mecânica:
Depois vamos igualar a zero:
Repare que a nossa equação é do segundo grau, então teremos duas posições de equilíbrio!!!
Para determinar essas posições de equilíbrio devemos igualar a equação que achamos à zero:
Podemos escrever a nossa equação dessa forma aqui:
Então, os valores de que tornam a nossa equação igual a zero são:
E essas são as posições de equilíbrio que estávamos procurando!!!
Passo 2
Agora vamos ver se essas condições são de equilíbrio estável ou instável. Para isso temos que derivar mais uma vez a nossa expressão de energia:
Agora temos que substituir os valores de que achamos para a posição de equilíbrio nesta equação aí de cima:
Como nosso resultado é maior que zero, então estamos na condição do equilíbrio estável:
E para , temos que:
Como obtemos um resultado menor que zero, então estamos na condição do equilíbrio instável:
Assim: quando será uma condição estável e quando teremos uma condição instável.
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 308, 7/36
A barra uniforme de massa e comprimento é sustentada no plano vertical por duas molas idênticas com rigidez e comprimidas de um comprimento na posição vertical, . Determine a rigidez mínima que garantirá uma posição de equilíbrio estável com Pode-se considerar que as molas atuam na direção horizontal durante um pequeno movimento angular da barra.
Passo 1
Podemos desenhar melhor esse problema assim:
Onde é o centro de gravidade da nossa barra!
Nós temos duas molas, não é mesmo? Quando a barra se deslocar em radianos, uma mola será comprimida e a outra será distendida. Assim, podemos dizer que existem duas energias potenciais elásticas uma para cada mola.
Para a mola que será esticada, vamos ter que:
Mas quanto vale ? Repare que é o comprimento inicial da mola que foi dito no enunciado que é mais o quanto a mola esticou que pelo nosso desenho vale , então:
E para a mola que será comprimida teremos que o é o comprimento inicial da mola que também é menos o quanto a mola comprimiu que é o mesmo , então:
Não podemos esquecer da energia potencial gravitacional:
Lembrando que é a altura do centro de gravidade da barra!!!
Então, a nossa energia potencial total será a soma destas três formas de energias que achamos:
Passo 2
Agora precisamos derivar a nossa equação da energia total:
Repare que precisamos usar a regra da cadeia!
Será que a posição é uma posição de equilíbrio, como diz o enunciado? Para verificar isso temos que substituir na equação que acabamos de achar:
Então, é uma posição de equilíbrio!!!
Passo 3
Agora vamos verificar a estabilidade e para isso precisamos derivar duas vezes a nossa equação da energia total:
Passo 4
Para que o equilíbrio seja estável, devemos ter:
Então, vamos achar o valor de mínimo para que isto aconteça quando :
Então, o menor valor possível para a rigidez da mola deve ser igual a:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 308, 7/38
O pequeno cilindro de massa e raio está confinado a rolar sobre a superfície circular de raio . Usando os métodos desta seção, prove que o cilindro é instável no caso e estável no caso
Passo 1
Vamos considerar que é o nível de energia potencial nula no nosso sistema. Então, podemos desenhar o caso assim:
A energia potencial gravitacional do cilindro é calculada pela seguinte fórmula:
Onde é a distância vertical do centro de massa do cilindro até o nosso ponto onde a energia potencial é nula:
Então:
Com isso conseguimos calcular a energia potencial gravitacional do cilindro:
Passo 2
No outro caso temos o seguinte:
E a altura do centro de gravidade do cilindro?
Por que está negativo? Porque a altura está abaixo da nossa referência que é quando .
Dessa forma, a energia potencial gravitacional será:
Passo 3
Vamos testar os dois casos. Para isso temos que derivar a equação da energia potencial.
Vamos começar com o caso . Sabemos que a energia potencial gravitacional neste caso é:
Então, a derivando isso com relação a vamos ter que:
Para termos equilíbrio precisamos igualar esta equação a zero, então:
O é zero em duas situações, quando:
Neste caso, tem que ser rejeitado porque não faz muito sentido. É como se a massa estivesse dentro da curva onde o cilindro se encontra.
Agora temos que derivar de novo para analisar a estabilidade:
Agora vamos substituir nesta expressão que acabamos de achar:
Repare que o resultado será negativo, então ele será sempre menor que zero e isso caracteriza a situação do equilíbrio instável!
Passo 4
Vamos fazer o mesmo processo para o segundo caso. A equação da energia potencial que achamos foi:
Agora vamos derivar ela com relação à :
Para termos equilíbrio precisamos igualar esta equação a zero, então:
O é zero em duas situações, quando:
Novamente vamos descartar a solução !
Agora temos que derivar de novo para analisar a estabilidade:
Agora vamos substituir nesta expressão que acabamos de achar:
Repare que o resultado será positivo, então ele será sempre maior que zero e isso caracteriza a situação do equilíbrio estável!
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 308, 7/39
A barra uniforme de massa e comprimento é articulada em relação a um eixo horizontal que passa pela sua extremidade e está presa a uma mola de torção, que exerce um torque sobre ela, onde é a rigidez da mola, expressa em unidades de torque por radianos, e é a deflexão angular em relação à vertical, medida em radianos. Determine o valor máximo de para o qual o equilíbrio na posição é estável.
Passo 1
A energia potencial associada à mola é dada por:
Repare que trocamos o por , pois neste caso temos rotação da mola!
E a energia potencial gravitacional da barra?
Bom, vai ser dada pelo produto da massa, da gravidade e da altura do centro de gravidade:
Para achar a altura do centro de gravidade vamos usar trigonometria:
Então:
Substituindo na nossa fórmula, vamos ter que:
Passo 2
A energia total será a soma das energias que achamos:
Passo 3
Agora temos que derivar com relação a a expressão da energia total que achamos:
Passo 4
Para que em exista uma equilíbrio devemos ter que:
Vamos ver se esta condição já foi satisfeita:
Então, a condição para ter equilíbrio foi satisfeita!
Passo 5
E para que este equilíbrio seja estável precisamos atender a esta condição aqui:
Então, vamos ter que derivar novamente a nossa expressão da energia total:
Agora vamos ver qual a condição para termos o equilíbrio estável:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 309, 7/41
Duas barras idênticas estão soldadas em um ângulo de e são articuladas em , como mostrado. A massa do apoio é pequena em comparação à massa das barras. Investigue a estabilidade da posição de equilíbrio mostrada.
Passo 1
Vamos considerar a massa das duas barras juntas igual a . Então, cada barrinha terá a metade desta massa:
Não se esqueça que a massa do apoio é desprezível!!!
Vamos primeiro determinar o centro de gravidade do conjunto usando esta fórmula aqui:
Repare que é:
Então, vamos ter que:
Passo 2
A força de reação está sendo aplicada em . Assim, vamos calcular a energia potencial do corpo em relação ao ponto :
Esse é a distância vertical do centro de gravidade até o ponto que é a nossa referência:
Então, vamos ter que:
Repare que o sinal negativo é porque estamos indo contra o sentido do eixo que criamos!
Agora podemos calcular a energia potencial do corpo em relação ao ponto :
Passo 3
Agora vamos calcular a derivada da energia potencial em relação ao ângulo:
Para vamos ter que:
Agora vamos derivar mais uma vez a equação que achamos:
Para vamos ter que:
Então, a estrutura está estável!!!
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 319, 7/45
Um dos requisitos críticos no projeto de uma perna artificial é prevenir que a junta do joelho flambe sob carga quando a perna está esticada. Como uma primeira aproximação, simule a perna artificial como duas barras leves com uma mola de torção em seu ponto de união. A mola realiza um torque , que é proporcional ao ângulo de inclinação na junta. Determine o valor mínimo de que garantirá estabilidade da junta do joelho para .
Passo 1
O sistema pode ser representado assim:
Mas repare que temos um triângulo com dois lados iguais a , então o triângulo é isósceles e tem dois ângulos iguais:
Repare que o maior ângulo do nosso triângulo isósceles é igual a:
E sabendo que a soma de todos os ângulos internos de um triângulo deve ser igual a , vamos ter que:
Beleza?
Então, teremos o seguinte sistema:
Vamos considerar o nosso referencial de energia potencial gravitacional nula como indicado na figura!!!
Passo 2
Temos duas energias potenciais...
A primeira é a energia potencial gravitacional:
O é a distância da massa até o nosso referencial, no nosso caso vamos ter que:
Então:
E a segunda é a energia potencial elástica:
Então, para acharmos a expressão da energia total é só somarmos cada uma das energias:
Passo 3
Agora precisamos derivar esta equação com relação ao ângulo :
Repare que tivemos que aplicar a regra da cadeia nesta derivada!
Para achar a posição de equilíbrio, temos que igualar a equação que achamos a zero:
Para obtermos zero como resultado, o valor de deve ser zero. Então, a nossa posição de equilíbrio é:
Passo 4
Agora queremos saber o valor mínimo de para que o equilíbrio seja estável. Então, vamos ter que derivar duas vezes a nossa equação da energia potencial total:
Repare que tivemos que aplicar a regra da cadeia nesta derivada!
Sabemos que nossa posição de equilíbrio é , então vamos substituir isso na equação que acabamos de achar:
Para que o equilíbrio seja estável vamos ter que:
Então, o valor mínimo de será:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 310, 7/51
Uma extremidade da mola de torção está presa ao chão em e a outra extremidade está presa ao eixo em . A rigidez à torção da mola elástica é o torque necessário para torcer a mola de um ângulo de um radiano. A mola resiste ao momento em torno do eixo, causado pela força de tração no cabo enrolado ao redor do tambor de raio . Determine o valor de equilíbrio de medido a partir da posição tracejada, na qual a mola não está torcida.
Passo 1
O sistema pode ser representado pelo desenho abaixo:
Passo 2
Temos duas energias potenciais...
A primeira é a energia potencial gravitacional:
E a segunda é a energia potencial elástica:
Então, para acharmos a expressão da energia total é só somarmos cada uma das energias:
Passo 3
Agora precisamos derivar esta equação com relação ao ângulo :
Como o sistema está em equilíbrio precisamos igualar a zero a equação que acabamos de achar:
A distância que a corda andou corresponde ao comprimento :
Substituindo isso na expressão que achamos, vamos ter que:
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 310, 7/50
O sistema formado por uma barra leve articulada, a massa da extremidade e a mola, de rigidez são mostradas em sua posição de equilíbrio. O parâmetro é uma fração situada na faixa . Mostre que o sistema é estável para todos os valores de na faixa permissível.
Passo 1
Vamos primeiro usar o equilíbrio de momentos para descobrir o deslocamento da mola, , para a situação em que o ângulo vale
Temos:
Mas sabemos que a força elástica é calculada pela seguinte equação:
Assim:
Onde é a distensão da mola quando a barra está na horizontal
Passo 2
Agora vamos analisar o problema para um caso em que
Veja que o nível zero da energia potencial está no centro de giro da barra, ou seja, no ponto . Assim, a energia potencial da massa será:
Onde é a distância do centro de gravidade da massa até o nosso ponto de referência que é onde , então:
Repare que o sinal é negativo, pois o centro de gravidade está abaixo do nosso referencial!
Então, a energia potencial gravitacional será:
Já a energia potencial da mola, será:
Onde é o comprimento da mola quando a barra está na horizontal mais o quanto ela esticou que é :
Então, a energia potencial elástica é:
Agora somamos a energia potencial gravitacional e a elástica para acharmos a energia potencial total ():
Arrumando isso melhor, vamos ter que:
Passo 3
Agora temos que derivar esta equação que achamos:
Para que haja equilíbrio, devemos igualar o que achamos a zero:
Para que nossa expressão seja zero, devemos ter que:
Ou seja, em há equilíbrio. Partimos do caso geral e descobrimos que é a posição de equilíbrio.
Passo 4
Vamos derivar duas vezes a expressão da energia total:
E precisamos substituir para vermos o que acontece:
Como é sempre maior que zero da mesma forma que e também serão, então podemos dizer que:
para