Forças em Duas Dimensões
Produzido por Pablo RicardoTeoria
Introdução
Você já brincou de cabo de guerra? Nessa brincadeira existem duas equipes dispostas em linha reta, cada um deve dar o seu máximo para puxar o seu lado da corda e a equipe que fizer a maior força vence:
Esse o conceito mais intuito de força que temos. E é justamente sobre esta grandeza que vamos tratar neste tópico.
Então, partiu?
Componentes e projeções: Eixos retos
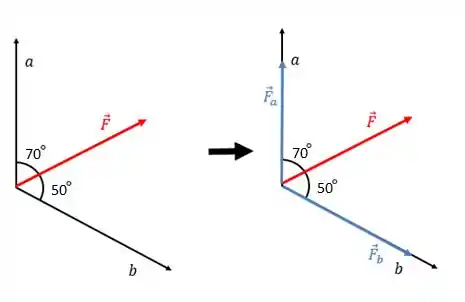
Primeiramente vamos falar sobre forças em apenas duas dimensões. Isso quer dizer que os vetores que representam essas forças possuem apenas duas componentes:
- Componentes
- Projeções
- Componentes
- Projeções
Eixos retos são eixos que fazem entre si, por exemplo, os eixos . Pra decompor uma força nesses eixos, basta trabalhar com senos e cossenos:
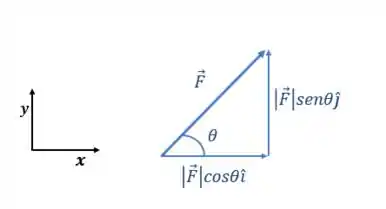
A forma correta de se escrever as componentes de uma força é escrevendo o módulo dela vezes o cosseno ou seno do ângulo, tudo isso seguido do vetor unitário. No caso dos eixos , usamos .
Não faça isso:
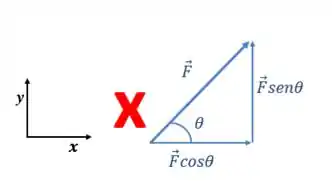
Afinal de contas, seria um vetor vezes um escalar. Isso não altera a direção de um vetor.
Para se calcular uma projeção em um eixo, basta você multiplicar o módulo do vetor pelo cosseno do ângulo que o vetor faz com esse eixo. E a direção? Bom, a direção da projeção será exatamente a mesma direção do eixo:
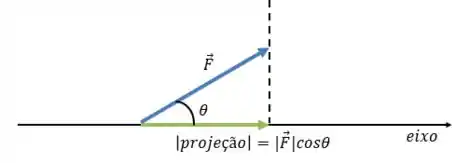
Essa é a forma de geral de se calcular a projeção em um eixo qualquer, não necessariamente o ou , mas lembre-se de sempre contar o ângulo no sentido horário, ok?
Componentes e projeções: Eixos com qualquer angulação
Quando os eixos possuem um ângulo entre eles que é diferente de como, por exemplo, , a coisa fica um pouco mais complicada. Nesse caso, temos que usar a lei dos senos.
A lei dos senos nos diz que, para um triângulo qualquer, temos a seguinte relação entre os lados e os ângulos:
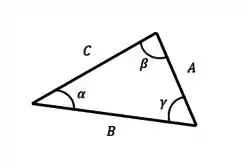
O bizu é você sempre dividir o lado pelo ângulo que tá “mirando” esse lado. Por exemplo, :
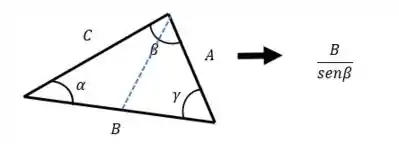
Mas como vamos usar isso em forças? Bom, nós vamos tentar formar esses triângulos com os vetores das componentes. Vamos ao exemplo de eixos que fazem entre si:
Queremos descobrir os módulos de . Sabemos que faz um ângulo de e de com os eixos e , respectivamente, e que as componentes estão em cima desses eixos.
Pra montar o nosso triângulo, basta a gente deslocar o vetor da componente para fechar o triângulo:
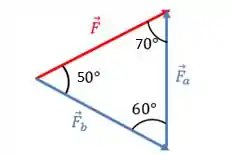
Show! Agora é só montar a equação:
E assim a gente descobre !!!
Em relação às projeções, não existem mudanças em relação aos eixos retos. Basta fazer a mesma coisa de sempre.
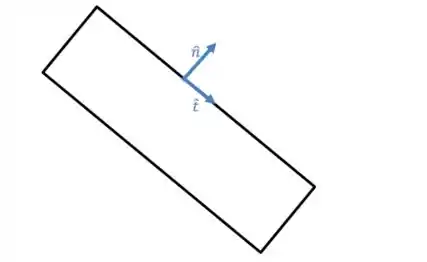
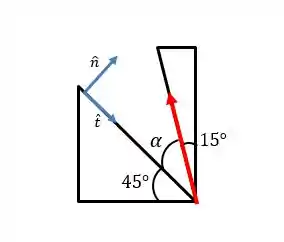
Componentes na direção normal e tangencial
Esse é um tipo especial de componentes retangulares. Muitas vezes o problema define uma direção perpendicular à superfície de um objeto (que vamos chamar de direção normal ) e uma direção tangencial () a ele, como na figura abaixo:
Com assim? Imagine que uma força esteja sendo aplicada em um carro:
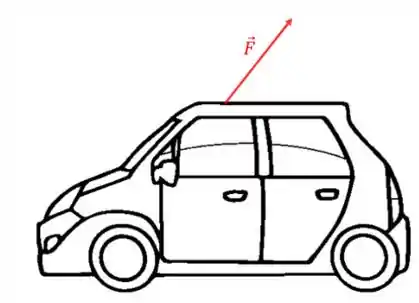
Podemos pensar que essa força é originada do vento, por exemplo.
E se você quiser saber qual componente dessa força é tangencial à superfície do carro? Ou seja, a “parte da força” que “escorrega”, ou “raspa” a superfície do carro?
Essa é a componente tangencial da força:
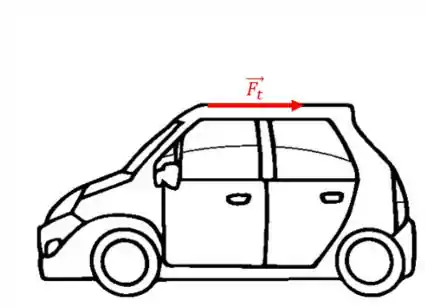
Costumamos denotar ela por .
E a componente normal? Bom, essa é a componente que é perpendicular à superfície. Ela é responsável por tracionar (puxar) ou comprimir(apertar) a superfície do corpo e geralmente a chamamos de
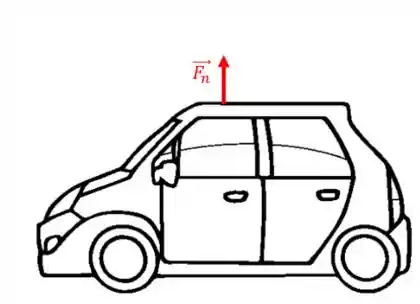
Quando representamos as duas, estamos representando uma força na direção normal e tangencial de um corpo:
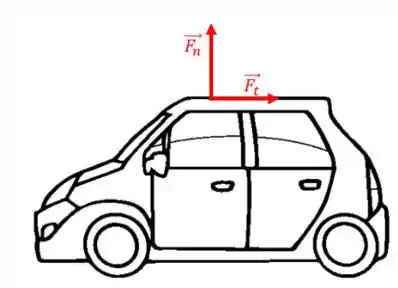
Nesse caso, vale tudo o que vimos para eixos retos. Os vetores unitários que representam as direções normal e tangencial são, geralmente, chamados de .
Escrevendo o vetor força por meio de sua linha de ação
Outra forma de se escrever o vetor de uma força é através dos pontos em que a linha de ação da força passa. Essa forma a gente vai usar bastante na parte da matéria.
Por exemplo, digamos que a linha de ação de uma força passe pelos pontos e
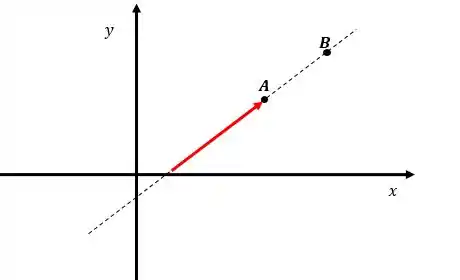
- O nosso primeiro passo é descobrir quem é o vetor que representa a direção. Para isso, basta a gente subtrair as coordenadas dos dois pontos:
- Agora vamos normalizar o vetor. O que isso quer dizer? Quer dizer vamos dividir o vetor pelo seu próprio módulo:
- E, por fim, você vai escrever o vetor força multiplicando o módulo da força, que geralmente é dado no enunciado desse tipo de questão, pelo vetor normalizado:
Exemplo: se tivermos as seguintes coordenadas para os pontos e , então:
Show?
Ah, e se a força estiver indo de para Nesse caso, devemos mudar o vetor para:
E fazer a mesma coisa que fizemos antes.
Onde, é o vetor normalizado.
No exemplo que fizemos antes, teríamos isso aqui:
Assim:
Por exemplo, digamos que a força seja de . Então:
Resultantes
Pra calcular a resultante de duas forças, nós temos que somar os dois vetores que representam as forças. Se tiver mais de dois vetores temos que fazer a mesma coisa.
Aí você já sabe, né? Podemos usar ou a soma de componentes ou a regra do paralelogramo, como vimos no tópico de vetores:
ou
No caso da regra do paralelogramo, caso a gente tenha mais de dois vetores, vamos ter que aplicar a regra de dois em dois vetores.
Por exemplo: aplique a regra nos vetores e , ache a resultante e depois aplique a regra em
E é isso. Vamos praticar um pouco agora?
Componentes e projeções: Eixos com qualquer angulação
Componentes na direção normal e tangencial
Escrevendo o vetor força por meio de sua linha de ação
Resultantes
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 25.2/4
A linha de ação da força de passa pelos pontos , como mostrado na figura. Determine os componentes escalares e de
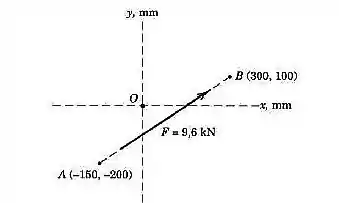
Passo 1
Primeiro vamos descobrir quem é o vetor que representa a direção . Para isso, vamos subtrair as coordenadas dos dois pontos:
Passo 2
Nosso próximo passo é achar o módulo deste vetor, ou seja, o seu tamanho. Para isso, temos que:
Passo 3
Agora vamos normaliza-lo! Isso vai ser importante na etapa de representação da força e, além disso, vai nos dar um vetor adimensional e unitário que representa a direção. Para isso, vamos dividir o vetor pelo seu módulo:
Passo 4
Agora, podemos escrever a força multiplicando-a pelo vetor normalizado:
Perceba que eu coloquei a força em Newtons, não em
Assim, os componentes escalares são:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 25.2/6
A força de é aplicada à extremidade da viga em Expresse como um vetor em termos de e j.
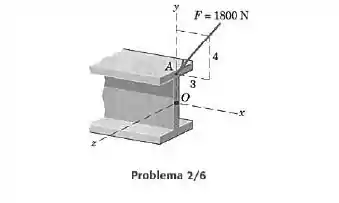
Passo 1
Podemos fazer da seguinte forma: Vamos calcular qual é o ângulo que a força faz com o eixo Depois vamos calcular as componentes escalares e e, por fim, escrever a força em função delas e dos vetores unitários.
Passo 2
O enunciado nos deu uma figura e, nessa figura, existe um triângulo. O ângulo que a força faz com o eixo é semelhante ao ângulo que o triângulo possui:
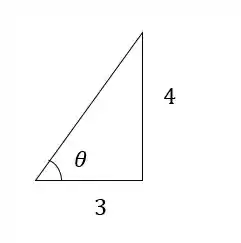
A tangente desse ângulo vale:
Assim, o ângulo vale:
Passo 3
Agora podemos calcular o módulo das componentes da força nos eixos (perceba que tais componentes estão orientadas no sentido negativo de seus eixos):
Passo 4
Assim:
Resposta
Exercício Resolvido #3
E J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 27.2/17
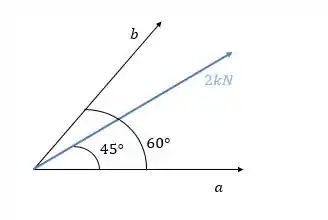
Determine as componentes da força de ao longo dos eixos oblíquos e . Determine as projeções de sobre os eixos e
Passo 1
Vamos começar pela projeção mais fácil: A do eixo , Vamos lembrar que vamos projetar o vetor ao longo do eixo , como se fosse a sombra desse vetor.
Como sabemos exatamente qual é o ângulo que a força faz com o eixo , podemos simplesmente multiplicar a força pelo cosseno desse ângulo:
Isso pode ser mostrado visualmente como:
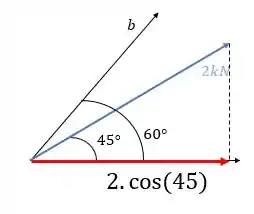
Essa força em vermelho é uma das componentes da força de ! Componente nada mais é do que dividir um vetor em outros eixos, olha só um caso geral:
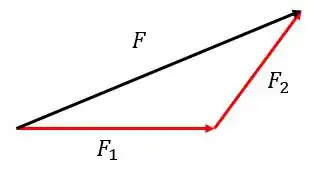
Aqui a força dividi-se em duas componentes e . Observe também que a soma dessas componentes é a própria força .
Passo 2
Já pra calcular a projeção da força no eixo , basta a gente perceber que o ângulo que a força faz com esse eixo vale
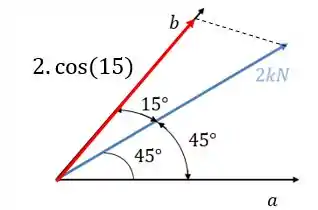
Podemos olhar também apenas as partes importantes para esse caso:
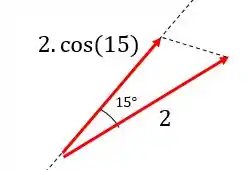
Afinal de contas, . Assim, podemos dizer que a projeção de no eixo vale:
Passo 3
Para achar as componentes, vamos usar a lei dos senos, já que os eixos não são os eixos
As componentes da força nas direções estão representadas abaixo:
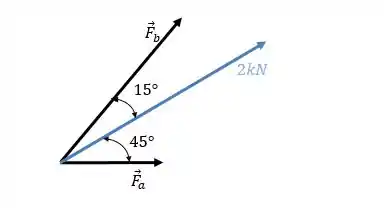
Perceba que componente e projeção são termos distintos, a soma das componentes sempre vai dar o vetor original!! Enquanto a soma das projeções (das sombras) irá dar um valor diferente da força (pelo fato dos eixos não serem perpendiculares)
Se deslocarmos o vetor (que é a componente de em ), mantendo a sua direção e sentido, formamos o seguinte triângulo:
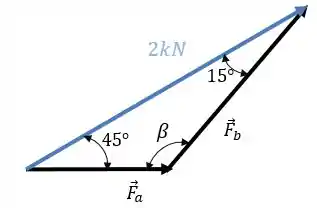
Não sabemos quanto vale , mas como a soma dos ângulos internos de um triângulo é sempre igual a
Assim:
Pela lei dos senos:
Assim:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 27.2/18
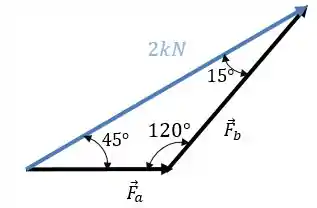
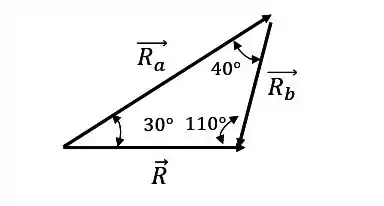
Determine os componentes retangulares e da força ao longo dos eixos não retangulares e . Determine também a projeção ortogonal de sobre o eixo .
Passo 1
As componentes que queremos achar e a força podem ser vistas abaixo:
Passo 2
Se deslocarmos o vetor , sem mudar a sua direção e sentido, podemos formar o seguinte triângulo:
Nós não sabemos o ângulo , mas sabemos que a soma dos ângulos internos de um triângulo é sempre igual a , então:
Assim:
Passo 3
Show de bola! Agora vamos aplicar a nossa famosa lei dos senos: Pra cada lado do triângulo, escolha o ângulo que lhe é oposto e monte a equação:
Como sabemos o valor de , basta a gente isolar o que não sabemos:
Passo 4
A projeção de sobre o eixo é mais fácil de se fazer. Basta multiplicar o módulo de pelo cosseno do ângulo que a força faz com o eixo
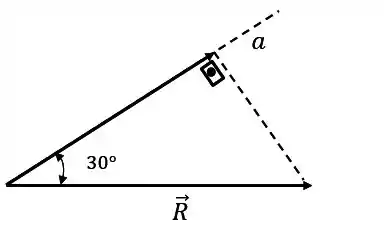
Assim:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 27.2/19
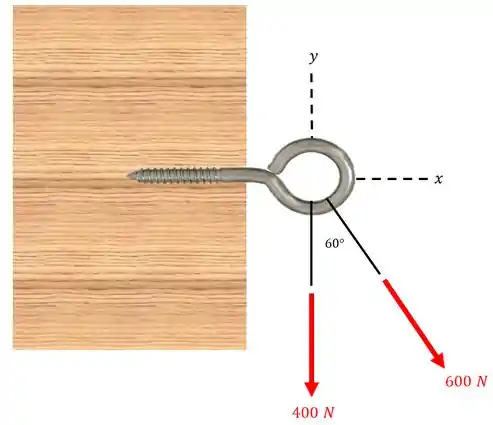
Determine a resultante das duas forças mostradas.
- Aplicando a regra do paralelogramo.
- Somando as componentes escalares.
Passo 1
Finalmente vamos usar a nossa querida regra do paralelogramo!!
Nesse caso, é claro, vamos encontrar apenas o módulo da força resultante.
Aplicando a regra:
Passo 2
Agora vamos decompor as forças em suas componentes escalares.
A força de é claramente vertical e aponta no sentido negativo de , assim:
Já a força de precisa ser decomposta segundo o triângulo abaixo:
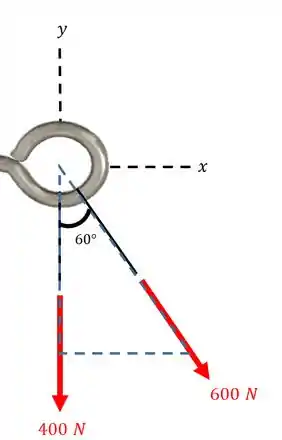
A força faz um ângulo de com o eixo , nesse caso. Mas isso não nos atrapalha, não é mesmo? É Só notar que a componente horizontal será e a vertical . Assim:
Assim, a força resultante será:
E o módulo:
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 26.2/13
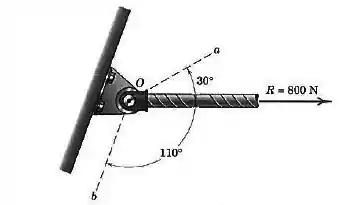
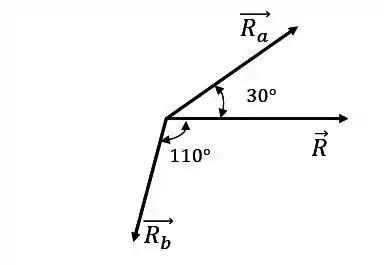
As duas forças mostradas atuam no ponto da barra dobrada. Determine a resultante das forças.
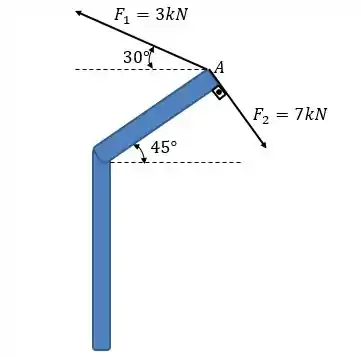
Passo 1
Nessa questão você quer saber a resultante das forças que atuam em , ou seja, a soma das forças.
A forma mais fácil de se fazer isso, novamente, é pela soma das componentes das forças. Então, nosso primeiro trabalho vai ser escrever essas forças em termos de vetores
Passo 2
Vamos analisar primeiro a força de
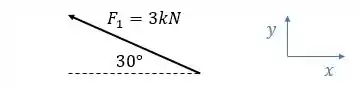
A força faz um ângulo de com o sentido negativo do eixo ( o que corresponderia a com o sentido positivo do eixo).
Assim, a componente horizontal do vetor será negativa. Podemos dizer que a força pode ser escrita por:
Passo 3
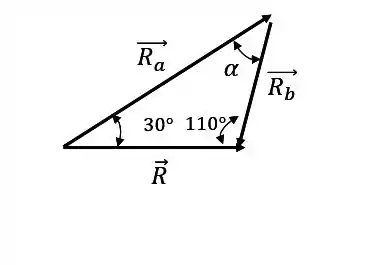
Agora vamos olhar para a força de o ângulo que ela faz com o eixo positivo não está explicito, mas podemos calculá-lo:
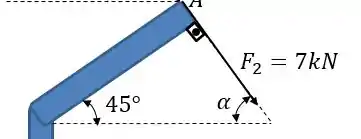
A soma dos ângulos internos de um triângulo tem que dar , certo? Então:
Assim, o ângulo vale . Perceba que: a força aponta para baixo, logo, a componente vertical é negativa.
Ela aponta para frente, logo a componente horizontal é positiva.
Assim:
Passo 4
A resultante será:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 26.2/11
O componente da força vale . Determine o componente (normal) e o módulo de
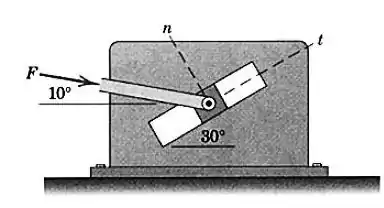
Passo 1
O sistema de forças pode ser representado por:
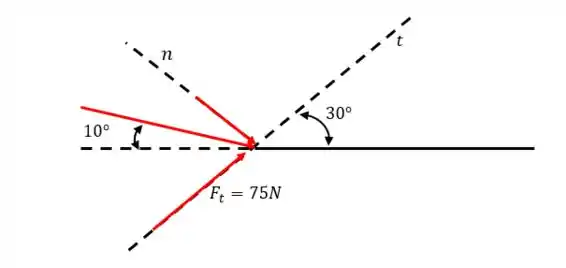
Nós só sabemos quanto vale a componente tangencial da força e queremos saber quanto vale a componente normal e o módulo da força total.
Passo 2
Vamos analisar os ângulos:
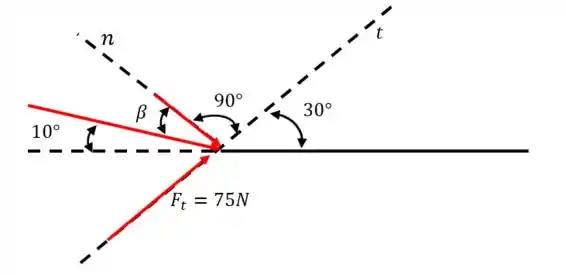
Não sabemos quanto vale , mas como a soma dos ângulos na figura tem que ser igual , podemos dizer que:
Passo 3
Agora, se arrastarmos o vetor tangencial, podemos formar o seguinte triângulo:
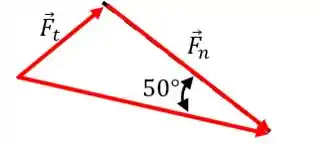
Pela definição de tangente, podemos escrever:
E a direção? Pela figura, a componente normal está orientada no sentido negativo do eixo normal. Assim:
Passo 4
De novo no triângulo anterior, perceba que a relação entre o módulo da força e o módulo da componente normal é dada por:
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 29.2/27
Os cabos de sustentação eestão presos no topo da torre de transmissão. A força trativa no cabo vale . Determine a força trativa necessária no cabo , tal que o efeito resultante das duas trativas nos cabos seja uma força direcionada para baixo no ponto Determine o módulo dessa força.
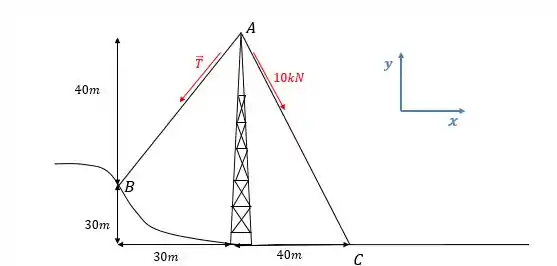
Passo 1
Primeiro vamos escrever as forças em componentes . Para isso, perceba que existem triângulos retângulos na figura que nos irão ajudar a achar os ângulos que as forças fazem com o eixo
Para força de , temos o triângulo:
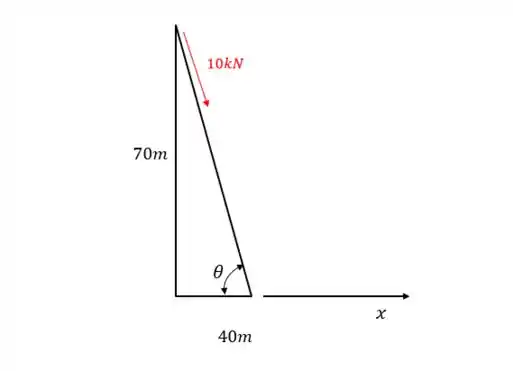
Assim, chamando a força de , ela poderá ser escrita como:
Perceba que eu coloquei o sinal de negativo, pois a força aponta para baixo, já que estamos analisando o ponto e ele está sendo puxado para baixo (chamamos isso de tração).
Pra achar o ângulo, basta fazermos:
Assim, a força será:
Passo 2
E a força Bom, nesse caso, o triângulo representativo que temos é:
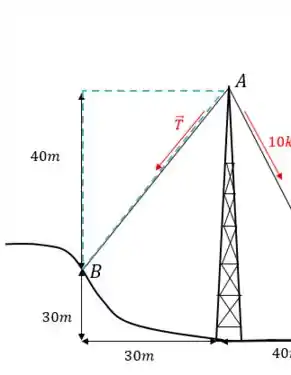
Ou seja:
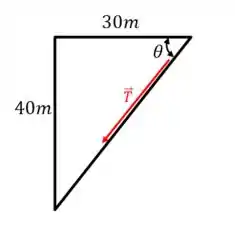
O ângulo vale:
E já que a tensão aponta no sentido negativo do eixo
Passo 3
Agora vem a parte que precisamos raciocinar mais: se a força resultante deve apontar apenas para baixo, ela não deve possuir uma componente na direção , certo?
Como vamos somar a força e a força de , podemos dizer a soma das componentes dessas forças em é nula:
E esse é o módulo da força necessária.
Passo 4
Para achar a resultante , basta a gente somar as componentes das forças:
E ela aponta para baixo, como era esperado!!!
O módulo dessa força vale:
Isso porque ela só possui uma componente.
Resposta
Exercício Resolvido #9
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 26.2/12
Uma força de módulo é aplicada ao ponto da barra , como mostrado. Determine os componentes e de
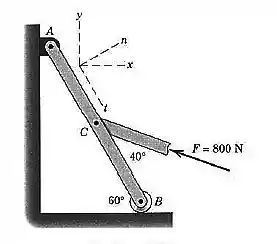
Passo 1
Precisamos descobrir quais são os ângulos que a força de faz com os eixos e.
Para isso, vamos ter que usar um pouco de geometria, como fizemos antes.
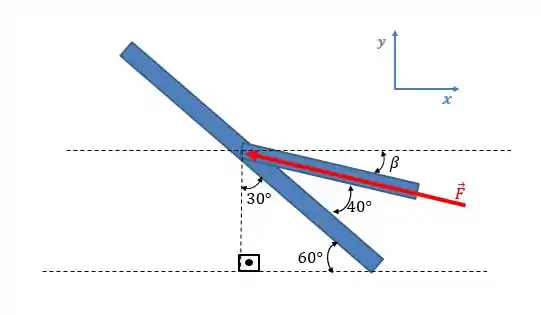
Vamos interpretar o desenho: o triângulo inferior tem dois ângulos agudos: e. O ângulo de foi dado no enunciado e o de foi calculado levando-se em consideração que o triângulo é retângulo:
Mas o ângulo que nos interessa é o ângulo . Para calculá-lo, basta você perceber que a soma dos ângulos de , e tem que dar . Assim:
Passo 2
Com esse ângulo, fica fácil descobrir as componentes
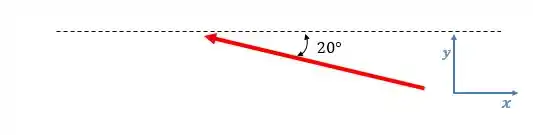
Assim, as componentes e , em módulo, serão:
Como dá pra ver pelo vetor, a componente aponta no sentido contrário do eixo . Assim, podemos escrever a força como:
Passo 3
E as componentes tangencias e normais? Essas são mais fáceis nesse problema pois o ângulo de é tudo que precisamos:
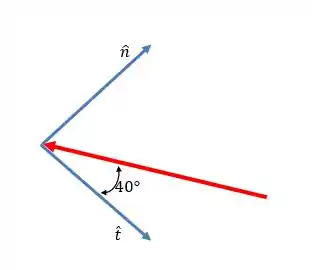
Assim:
E os sentidos? Dá para ver, pela figura, que ambas as componentes são contrárias aos sentidos positivos dos eixos. Assim, a força pode ser escrita assim:
Resposta
Exercício Resolvido #10
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 28.2/26
No projeto de um robô para colocar, sem folga, a pequena parte cilíndrica em um furo circular, o braço deve exercer uma força de na peça, paralelamente ao eixo do furo, como mostrado. Determine as componentes da força que a peça exerce sobre o robô ao longo dos eixos paralelo e perpendicular ao braço e paralelo e perpendicular ao braço .
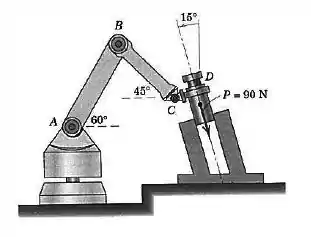
Passo 1
Essa questão vai nos dar um pouco mais de trabalho. O primeiro passo é perceber o que está sendo pedido: as componentes normais e tangenciais em cada trecho.
a)
Vamos desenhar dois triângulos que vão nos ajudar quais são os ângulos que a força faz com os eixos do trecho
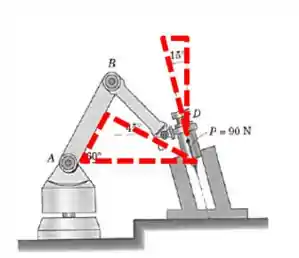
Agora vamos olhá-los separadamente, marcando os eixos e a força:
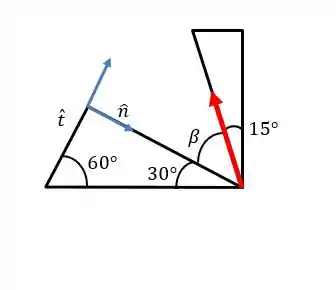
Perceba que o ângulo de está ali porque o primeiro triângulo é retângulo, assim como o segundo.
Outra coisa: Percebeu que a força tem o sentido contrário da força do enunciado? Isso acontece porque estamos analisando a força que a peça faz na estrutura, ou seja, é a reação da força do enunciado.
Passo 2
Para decompor a força, precisamos descobrir quanto vale o ângulo . Olhando a figura do passo anterior, dá para ver que a soma dos ângulos tem que dar , assim:
Agora ficou fácil:
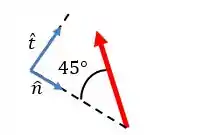
Podemos escrever a força como:
Passo 3
b):
Bora desenhar os triângulos na figura de novo:
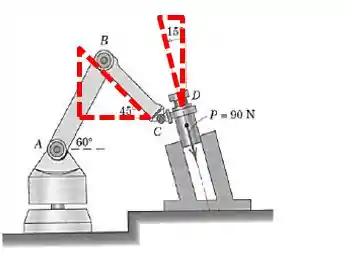
Analisando os triângulos separadamente e marcando a força e os eixos:
Quanto vale Já sabe, só se ligar que a soma dos ângulos tem que dar
Passo 4
Agora ficou fácil! Só fazer a decomposição usando o ângulo:
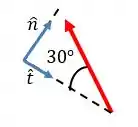
Assim:
Resposta
a)
b)