Momentos em Duas Dimensões
Produzido por Pablo RicardoTeoria
Introdução
Você já tentou fechar uma porta empurrando pela parte mais próxima as dobradiças?

Tem que fazer uma força danada, não é mesmo?
Em compensação quando você empurra a porta pela maçaneta não é necessário fazer tanta força. Por que isso ocorre?

Repare que quando você empurra a porta perto da dobradiça, você está aplicando uma força a uma distância bem pequena do eixo em torno do qual a porta gira, não é mesmo? E quando você aplica uma força na maçaneta essa distância aumenta.
Qual a relação entre a intensidade da força e a distância do ponto de aplicação? É justamente isso que vamos aprender neste capítulo. Partiu?
Momento
Além da capacidade de movimentar um corpo em uma direção, uma força também possui a capacidade de girar um corpo em relação a um eixo. Essa tendência de provocar rotação se chama momento () e o seu módulo é calculado pela seguinte equação:
Onde, é a intensidade da força aplicada e é chamado braço de alavanca que é a distância perpendicular ao eixo de rotação até qualquer ponto da linha de ação da força.
O momento é dado em unidade de força vezes a unidade de distância, sendo a que unidade mais usada é .
O momento é um vetor perpendicular ao plano do corpo que se está analisando e para definir seu sentido usamos a regra da mão direita, como veremos mais adiante.
Vamos ver um exemplo: imagine que você aplique uma força na maçaneta da porta:
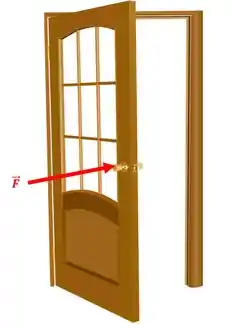
O eixo de rotação da porta é na dobradiça junto da parede:
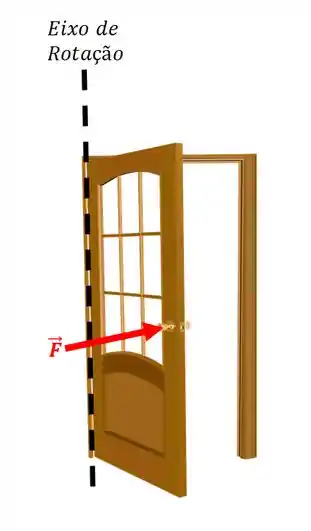
Então, o módulo do momento dessa força com relação ao eixo de rotação será:
Onde a é distância do ponto onde a força foi aplicada (maçaneta) até a dobradiça da porta:
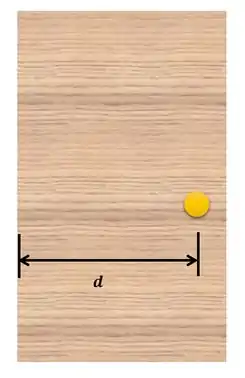
Momento pelo Teorema de Varignon
Esse é o método que você vai usar mais! Além disso, sem dúvida é o mais fácil e útil.
O teorema de Varignon nos diz que se uma força é definida por duas componentes:
O momento total daquela força, em relação a um ponto, é igual à soma dos momentos de cada componente:
Vamos ver outro exemplo prático: uma força atua numa aresta de uma caixa.
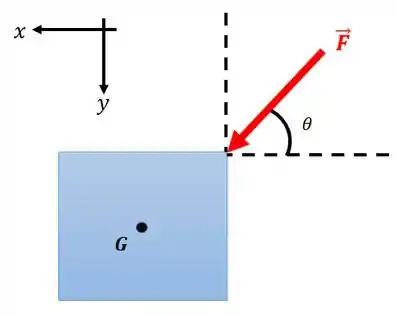
Essa força tende a girar a caixinha em torno do seu centro de gravidade . Mas para calcular o momento que esta força faz com relação ao ponto seria mais complicado, pois a força está inclinada.
Então, o que vamos fazer é decompor esta força nos eixos e . Essa força pode ser decomposta em duas componentes:
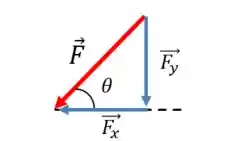
E para calcular o momento de cada força?
Primeiro você precisa definir um sentido positivo de giro para o momento: horário ou anti-horário. Vamos combinar aqui que o sentido positivo será o anti-horário.
Feito isso, multiplique o valor de cada componente pela sua respectiva distância perpendicular à linha de ação da força até o ponto .
Vamos com calma. Vamos fazer primeiro para a componente no eixo :
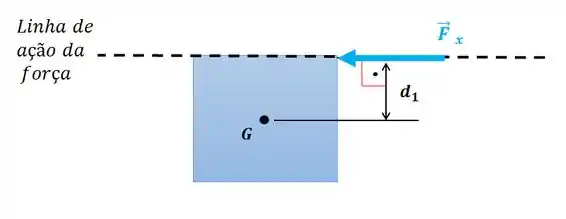
O momento da componente com relação ao ponto será:
O sinal do momento é definido pela regra da mão direita. Para isso, coloque os dedos da palma da sua mão direita no sentido que a setinha da força aponta e faça o movimento de girar em torno do ponto :
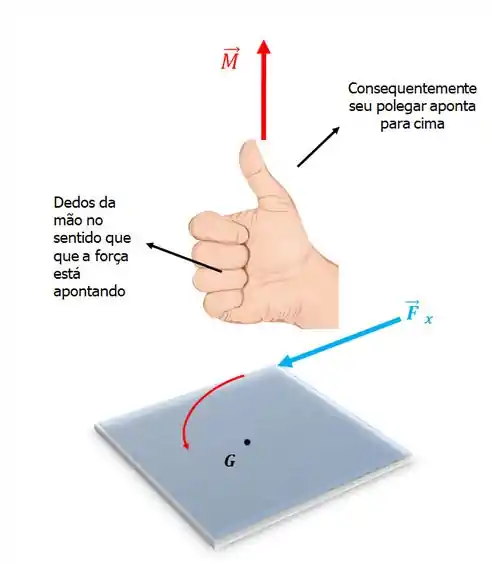
Perceba que a sua mão tende a fazer o movimento sugerido pela seta vermelha na figura acima. Ou seja, a força faz o bloco girar no sentido anti-horário, logo ela é positiva segundo a nossa convenção de sinais.
Agora a componente no eixo :
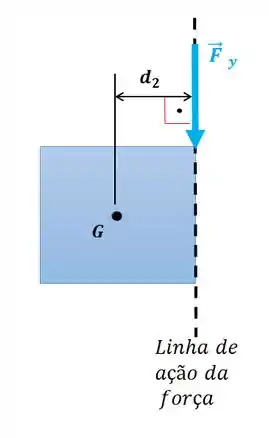
O momento da componente com relação ao ponto será:
Para determinar o sinal do momento, temos que usar a regra da mão direita de novo e neste caso ficaria assim:
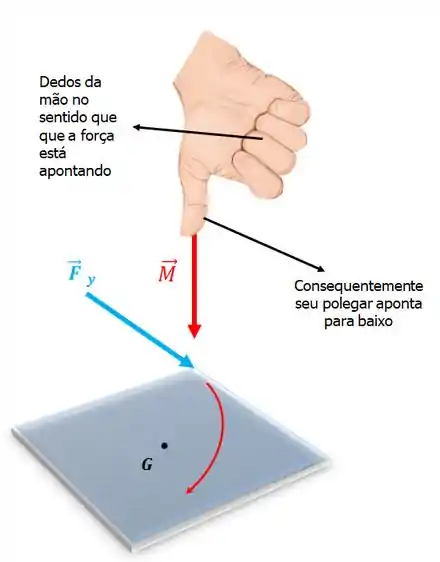
Como a força tende a fazer o bloquinho girar no sentido horário, o seu momento será negativo:
Para achar o momento total em torno do ponto é só somarmos o momento que cada componente da força faz:
Pronto, dessa maneira você consegue encontrar facilmente o valor final do seu momento. Faremos isso várias vezes nos exercícios.
Momento na forma vetorial
Em alguns problemas, você vai ter que dar um tratamento vetorial ao momento. Nesse caso, o momento vai ser representado pelo vetor gerado pelo produto vetorial abaixo:
Nesses casos, você vai fazer aquilo que aprendemos em vetores: usar o determinante abaixo para calcular isso:
Com esse produto você já consegue determinar o sentido do vetor, mas caso você queira conferir, só lembrar a regra da mão direita:
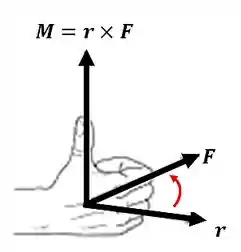
E é basicamente isso! Bora praticar?
Momento pelo Teorema de Varignon
Momento na forma vetorial
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 33-2/29
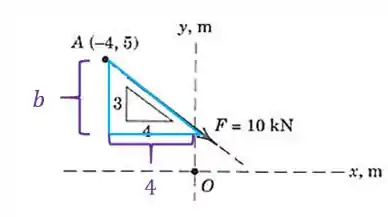
A força de é aplicada no ponto . Calcule o momento de em relação ao ponto . Determine os pontos nos eixos e em relação aos quais o momento de vale zero.
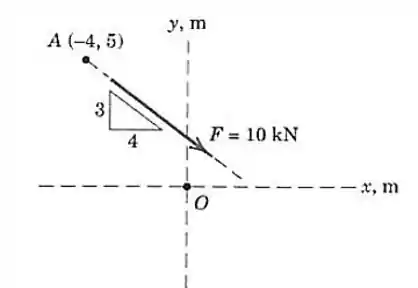
Passo 1
Vamos começar decompondo a força nos eixo e . Para isso temos que achar o ângulo de inclinação dessa força:
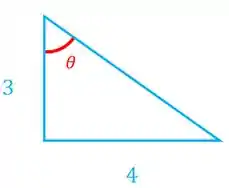
Agora podemos decompor a nossa força :
Passo 2
Agora vamos calcular o momento com relação ao ponto para cada uma das componentes separadamente. Vamos começar pela componente em :
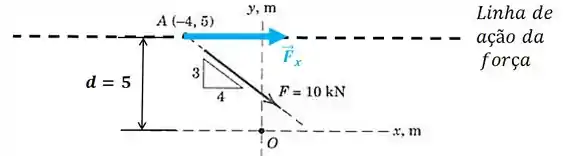
A distância perpendicular à linha de ação da força até o ponto é:
Então, o módulo do momento de com relação ao ponto é dado pelo módulo da força e a distância:
E para saber o sinal, temos que analisar...
Repare que a força gira no sentido horário em torno do ponto , então ela será negativa pela nossa convenção de sinais:
E a componente em ?
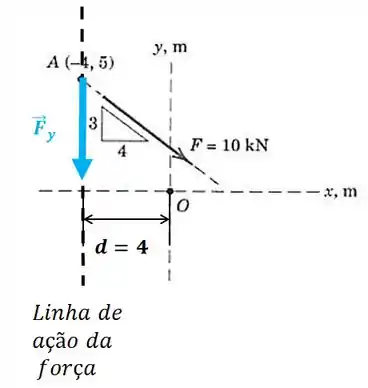
O módulo do momento desta força será:
E esse momento será positivo ou negativo? Repare que a força tende a girar em torno do ponto no sentido anti-horário, logo ela será positiva.
O momento total em relação ao ponto será igual a soma do momento que cada componente faz:
Ou seja, como esse valor deu negativo, o nosso momento total está no sentido horário!
Passo 3
Agora temos que ver onde nos eixos e o momento será zero. Pessoal, momento não é calculado como força vezes distância?
Então é só acharmos os pontos onda a distância da linha de ação da força ao eixo é zero!
Isso ocorre onde a linha de ação da força cruza esses eixos:
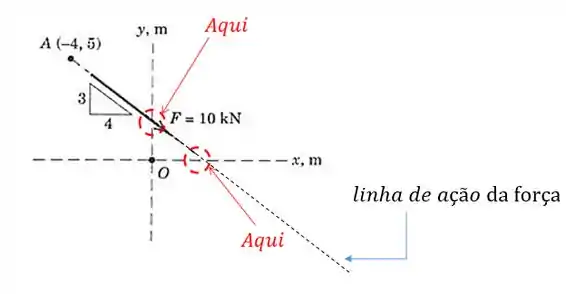
Repare que agora vamos utilizar a linha de ação da força e não mais apenas de suas componentes e .
Então, vamos usar semelhança de triângulos para obter esses valores. Vamos começar pelo eixo :
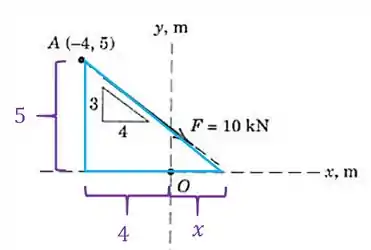
Vamos fazer a semelhança entre esses dois triângulos aqui:
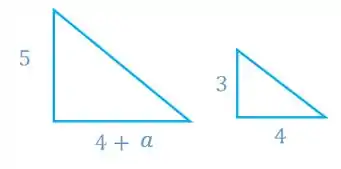
Então, a coordenada fica:
Ou seja
Vamos fazer outra semelhança de triângulos para achar o ponto onde intercepta o eixo :
Vamos ter os seguintes triângulos:
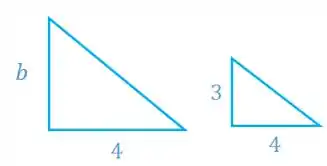
Então, a coordenada fica:
Repare que para achar esse valor também poderíamos ter feito a semelhança de triângulos usando 2,67. Ficaria assim:
Ou seja,
Resposta
Exercício Resolvido #2
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 33-2/30
Determine o momento da força de em relação ao ponto e em relação ao ponto .
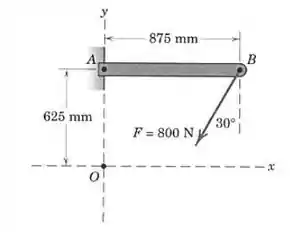
Passo 1
Vamos começar decompondo a força nos eixo e . Repare que a força forma o seguinte triângulo retângulo:
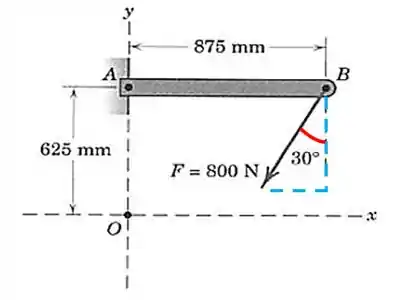
Vamos ter que:
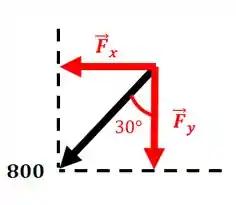
Passo 2
Agora vamos calcular o momento com relação ao ponto para cada uma das componentes separadamente. Vamos começar pela componente em :
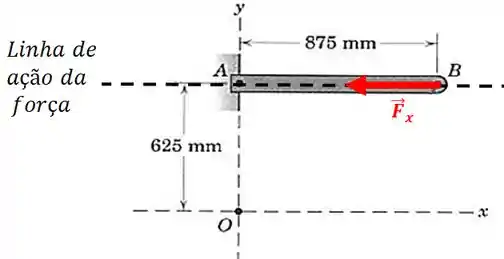
Qual é a distância perpendicular ao ponto até a linha de ação da força ? É zero!!!
Então,
E a componente em ?
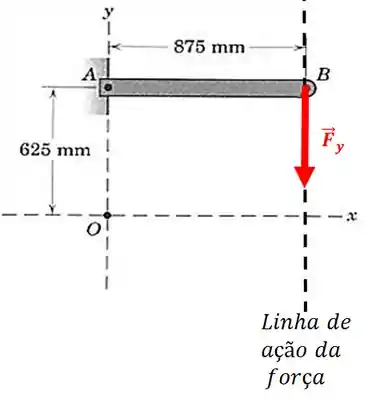
Agora sim existe uma distância do ponto até a linha de ação da força , então o momento desta força será:
E esse momento será positivo ou negativo? Repare que ele tende a fazer a barra girar no sentido horário, logo ele será negativo, pois seu dedão aponta para dentro da tela.
O momento total em relação ao ponto será igual a soma do momento que cada componente faz:
Passo 3
Agora vamos fazer o mesmo procedimento para calcular o momento com relação ao ponto . Vamos começar pela componente em :
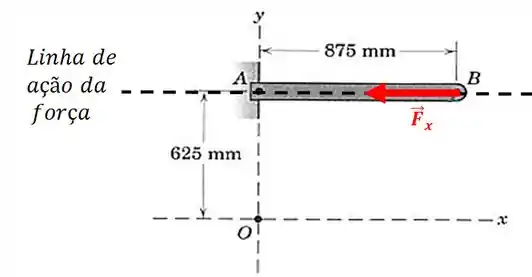
Repare que agora existe uma distância perpendicular à linha de ação da força até o ponto :
E esse momento será positivo ou negativo? Repare que ele faz a barra girar no sentido anti-horário em torno do ponto , então ele será positivo mesmo.
E a componente em ?
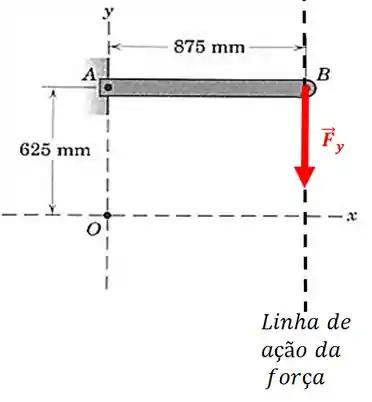
Repare que a distância perpendicular à linha de ação da força até o ponto será a mesma distância que usamos para o ponto . Então, o momento desta força com relação ao ponto será:
E o seu sinal também será negativo, pois tende a girar a barra no sentido anti-horário:
Então, o momento total com relação ao ponto será:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 33,2/31
Determine o momento da força de :
- Em relação ao ponto usando o teorema de Varignon.
- Em relação ao ponto por um enfoque vetorial.
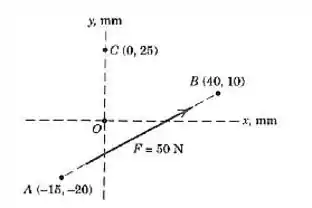
Passo 1
Vamos primeiro a escrever a força em termos dos vetores unitários e .
Pra isso, vamos determinar o vetor unitário da linha de ação da força. Esse vetor é o vetor unitário da distância entre
Assim:
Assim, a força é esse vetor multiplicado pelo módulo:
Passo 2
Vamos aplicar o teorema de varignon pra calcular o momento:
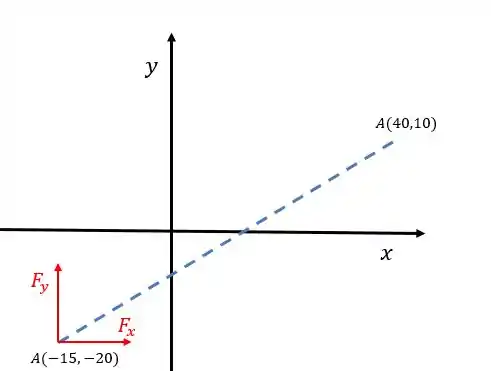
Observe a decomposição da força no ponto. Olhando o sentido de giro de cada componente( gira no sentido anti-horário e no horário) e adotando o sentido anti-horário como o positivo, temos:
Passo 3
b)
Agora queremos saber em relação ao ponto . Vamos usar um enfoque vetorial, ou seja:
E vamos usar a distância entre e como o braço de alavanca:
E :
Porém, nós vamos utilizar Laplace pra calcular o produto vetorial. Assim, é útil escrever os vetores com três dimensões, colocando a componente nula:
Assim:
Os dois primeiros determinantes dão zero, assim:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 34,2/34
O componente de controle do acelerador pivota livremente em Se uma mola de torção interna exerce um momento de retorno sobre o componente, quando ele está na posição mostrada, determine, para a finalidade de projeto, a força trativa necessária no cabo do acelerador para que o momento resultante em torno de seja zero. Observe que quando é zero, o componente se apóia no parafuso do ajuste da marcha lenta em
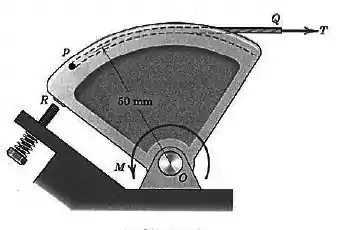
Passo 1
Essa questão é mais fácil do que parece: Basta que a gente interprete corretamente o problema.
O que sabemos? Sabemos que em existe um momento aplicado.
E o que queremos? Queremos que o momento total seja nulo, ou seja:
E o que faremos pra que isso corra? Aplicaremos uma força , distante de , que gere um torque de sentido contrário.
É importante você perceber pela figura do problema que essa força é tangencial ao componente de controle. Isso é muito bom pois isso significa que não precisamos decompor a força.
Passo 2
Temos:
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 41,2/64
Cada hélice de um navio de duas hélices desenvolve um empuxo de na velocidade máxima. Ao manobrar o navio, uma hélice está girando a toda velocidade para frente e a outra a toda velocidade no sentido reverso. Que empuxo cada rebocador deve exercer no navio para contrabalancear o efeito das hélices?
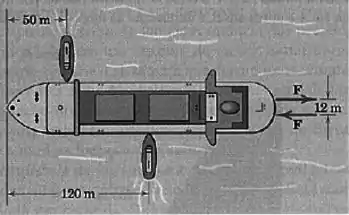
Passo 1
Primeiramente, vamos calcular o momento causado pelas forças
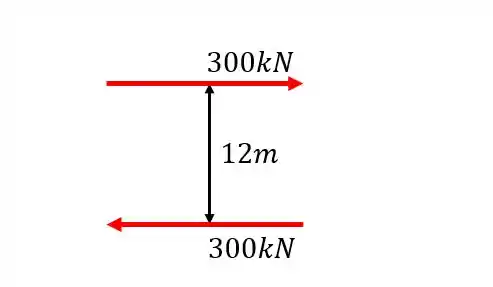
Assim:
Passo 2
Agora precisamos descobrir que empuxo cada rebocador deve exercer no navio pra contrabalancear esse momento. Ou seja:
Os momentos precisam ter o mesmo módulo.
Perceba que nesse caso cada rebocador tenderá a girar o navio em um sentido. Adotando o senti anti-horário como o positivo, teremos:
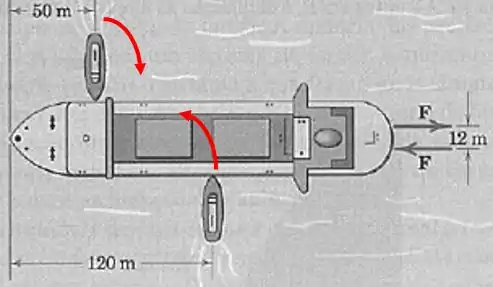
Assim:
Passo 3
Então:
Resposta
Exercício Resolvido #6
J.L. Meriam e L.G. Kraige, Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 33-2/35
A força de módulo é aplicada à roda dentada. Determine o momento de em relação ao ponto .
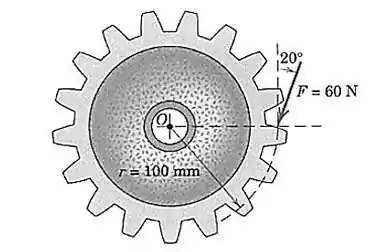
Passo 1
Nosso primeiro passo é decompor a força nos eixos e . Como podemos mover uma força ao longo da sua linha de ação sem alterar o problema, podemos fazer isso aqui para nos facilitar:
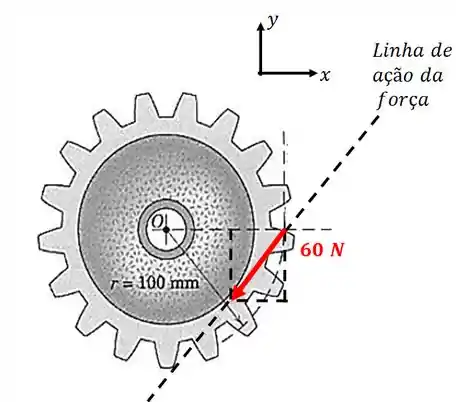
Temos o seguinte triângulo retângulo:
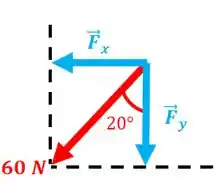
Então:
Passo 2
Agora vamos calcular o momento que cada componente faz em relação ao ponto . Vamos começar pela componente em :
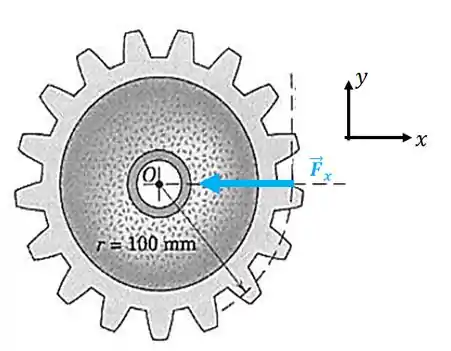
Repare que a distância perpendicular à linha de ação da força até o ponto é zero:
Agora vamos ver a componente em :
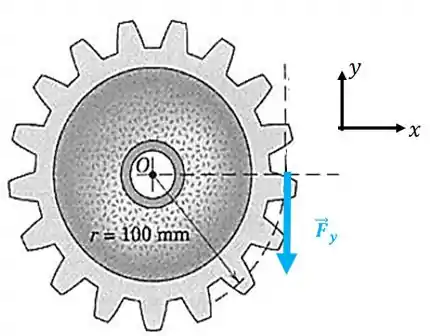
A distância perpendicular entre a linha de ação da força até o ponto é o raio da roda, então:
A força faz a roda girar em torno do ponto no sentido horário, logo esse momento é negativo:
Passo 3
O momento total em relação ao ponto será igual a soma do momento que cada componente faz:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 34,2/36
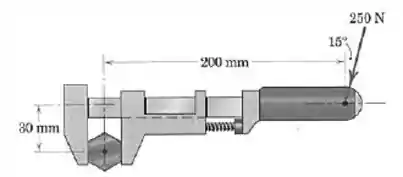
Calcule o momento da força de na manopla da chave inglesa em relação ao centro do parafuso.
Passo 1
Vamos calcular o momento pelas componentes:
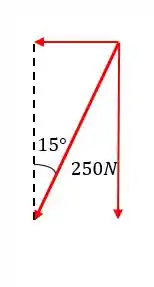
As componentes são:
Passo 2
tende a girar o parafuso no sentido anti-horário e no sentido horário. Adotando o sentido anti-horário como o positivo, temos:
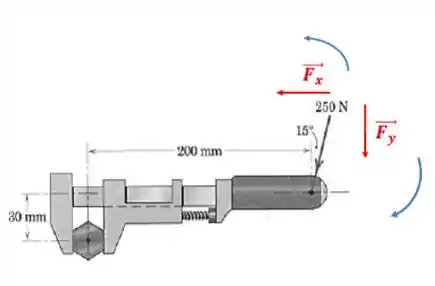
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 34,2/37
Um mecânico puxa a chave de boca de com a força de mostrada. Determine o momento da força em relação ao centro do parafuso.
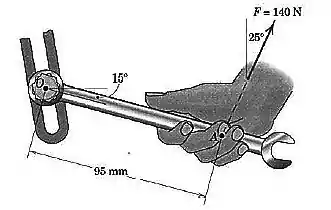
Passo 1
Vamos ter que pensar um pouco mais nessa questão aqui:
O problema dessa questão é que a barra de tem uma inclinação em relação à horizontal. É interessante, então, se a gente pudesse modelar esse problema sem essa inclinação.
Como assim?
Trabalhando com uma inclinação relativa.
Vamos chamar essa inclinação de
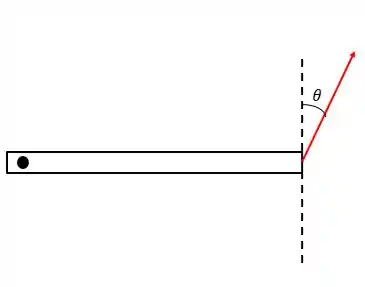
Passo 2
No desenho acima, não existe uma inclinação horizontal. Agora vamos inclinar a barra e ver o que acontece com a inclinação do vetor força lá na ponta da barra:
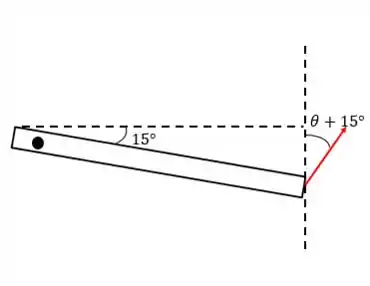
Com o giro de , a força também se inclina em a mais. Pelo enunciado, sabemos que esse ângulo final vale , assim:
Passo 3
Assim, podemos trabalhar com esse sistema:
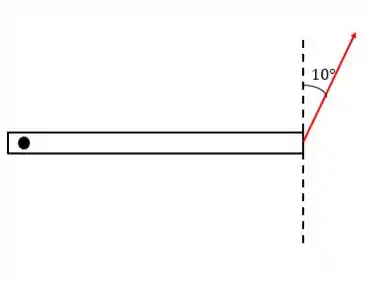
A componente () produzirá um momento nulo. Então vamos usar apenas a componente vertical. Assim:
Resposta
Exercício Resolvido #9
J.L. Meriam e L.G. Kraige,Mecânica para Engenharia, Estática, 6º ed. RJ: LTC, 2012, pp. 35-2/44
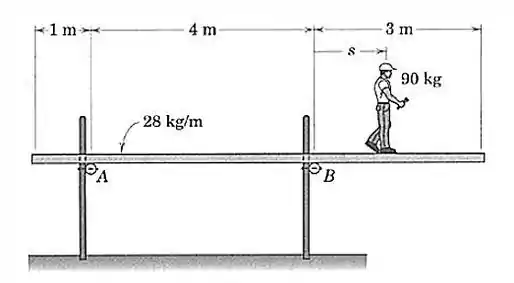
A plataforma uniforme, que tem uma massa por unidade de comprimento de , está simplesmente apoiada sobre barras de apoio em e em . Um trabalhador de construção civil com sai do ponto e anda para a direita. Em que posição o momento combinado do peso do homem e da plataforma será zero em relação ao ponto ?
Passo 1
Para resolver esta questão, vamos começar achando a força peso da plataforma e o seu ponto de aplicação. Repare que a placa tem de comprimento e foi dito no enunciado que ela possui por metro.
Então, a massa da plataforma () será de:
Vamos considerar a gravidade igual a , então o peso da plataforma () será:
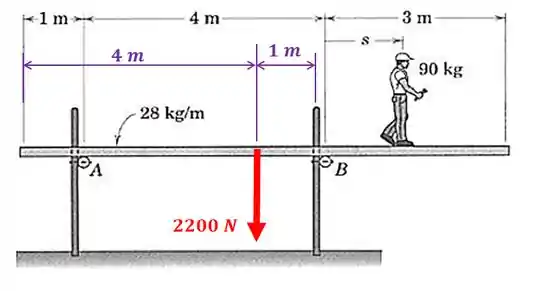
E onde esta força está aplicada? Foi dito no enunciado que a plataforma é uniforme, então a força está localizada no seu centro de gravidade, que neste caso é na metade do seu comprimento:
Passo 2
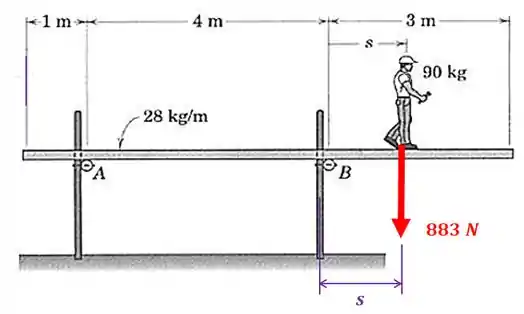
Agora vamos achar o peso do homem () que possui :
Passo 3
Vamos calcular o momento de cada uma dessas forças que achamos com relação ao ponto . Vamos começar pelo peso da plataforma:
Como esta força tende a girar no sentido anti-horário em torno do ponto , o momento que ela produzir será positivo, de acordo com a nossa convenção de sinais.
E o peso do homem? Nós não sabemos exatamente a distância que a força está do ponto , mas vamos chamar essa distância de :
Como esta força tende a girar no sentido horário, pela regra da mão direita seu polegar aponta para dentro da tela. Então, pela nossa convenção este momento será negativo:
Passo 4
A questão quer que o momento em torno do ponto seja zero, não é mesmo?
Mas sabemos que o momento em é igual a soma dos momentos produzidos com relação a este mesmo ponto por cada uma das nossas forças, então:
Resposta
Exercício Resolvido #10
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 35,2/47
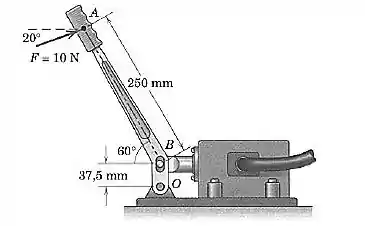
A força de é aplicada sobre a manopla da válvula de controle hidráulico, como mostrado. Calcule o momento dessa força em relação ao ponto
Passo 1
Diferentemente daquele outro exercício em que a barra também possuía um ângulo e nós resolvemos isso por meio de um ângulo relativo, nesse vamos fazer de uma forma mais bruta mesmo, só pra aprendermos duas formas diferentes.
O sistema do problema pode ser simplificado na figura abaixo:
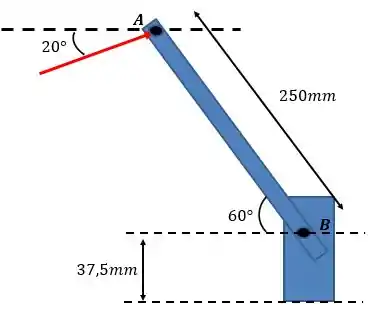
Passo 2
Vamos aplicar o teorema de Varignon, mas dessa vez vamos decompor a força e as distâncias.
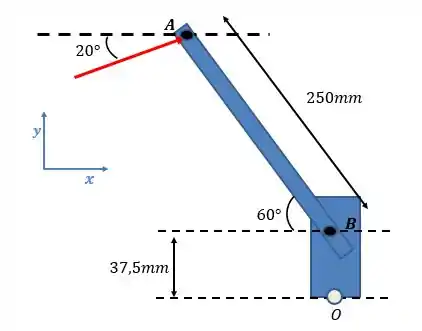
Decompondo a força na componente e as distância na componente :
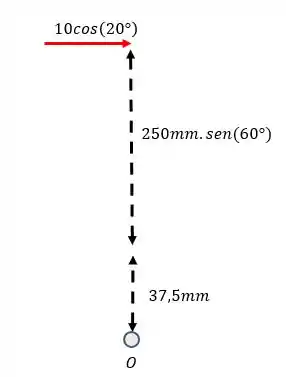
Adotando o sentido horário como o positivo, esse momento é igual a:
Passo 3
Decompondo a força na direção vertical e a distância na direção horizontal:
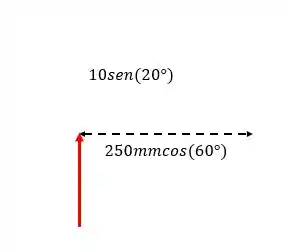
Assim:
Assim, o momento resultante vai ser a soma dos dois( já que eles têm o mesmo sentido):