Vetores
Teoria
Fala aí, você acabou de chegar no Responde Aí. E aqui, vamos tirar a sua dúvida sobre Vetores.
Grandeza escalar e vetorial
Quando você vai à padaria e diz “Me dê 10 pães”, a pessoa entende exatamente o que você quer, e você não precisa indicar qual é a “direção do pão”. Isso acontece pois é uma grandeza escalar.
Uma grandeza escalar, expressa a quantidade de alguma coisa. Algumas grandezas escalares famosas são: temperatura, massa, tempo, etc.
Agora vamos pra outra situação. Você está completamente perdido, e alguém diz “em 500 m tem uma parada de ônibus”. Mas pra qual direção? Você tem que ir pra esquerda? Pra direita? Tem que continuar andando em frente ou tem que voltar?
Essa confusão acontece, pois, deslocamento é uma grandeza vetorial! Quando falamos de grandezas vetoriais sempre precisamos indicar a direção e sentido, além da intensidade.
Outras grandezas vetoriais são: velocidade, força, aceleração, etc.
O que são os vetores?
Os vetores são a forma de indicar as grandezas vetoriais. Na prática, um vetor é representado por uma seta!
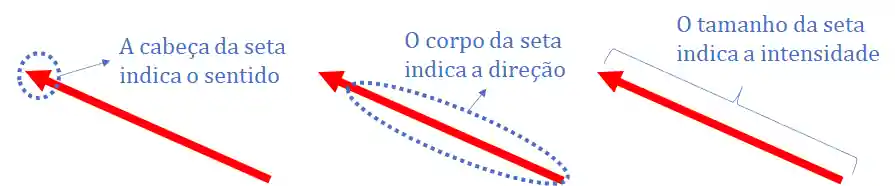
A seta aponta a direção e sentido do vetor, e o tamanho da seta representa a intensidade.
A intensidade também é chamada de módulo.
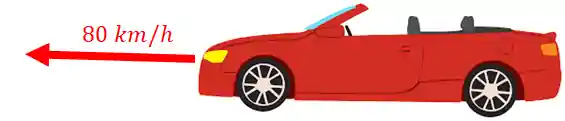
Por exemplo. Se eu disse que o meu carro se move a
Representando vetores matematicamente
Quando a gente for fazer contas, a gente precisa de formas fáceis de escrever vetores numa equação.
A forma mais comum de escrever um vetor é colocar uma setinha em cima da variável:
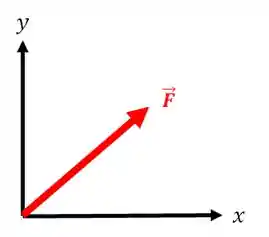
Decomposição de vetores
Mas para que você possa fazer cálculos com os vetores, é importante que ele seja representado em termos de suas componentes.
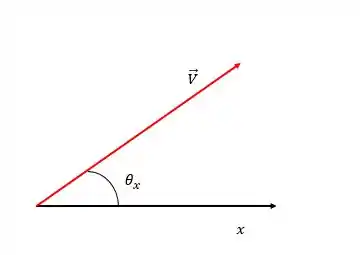
E o que são componentes? Veja esse vetor aqui embaixo:
Ele pode ser decomposto em uma componente no eixo
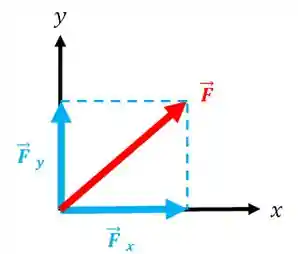
Podemos representar isso usando parênteses:
Se tivermos três dimensões nós usamos:
E como descobrimos o valor de
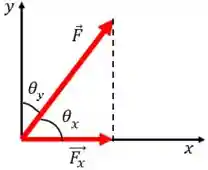
E com base nesses ângulos a gente calcula o módulo das componentes
Representando vetores usando vetores unitários
Outra forma de representar vetores é usando vetores unitários.
É bem simples, pra cada um dos três eixos
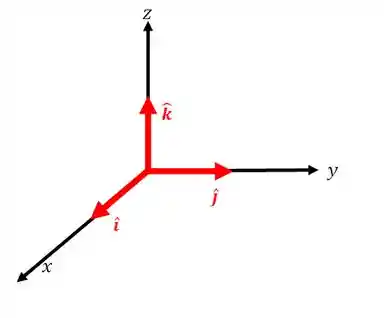
Então podemos representar um vetor da seguinte forma:
Módulo de um vetor
Outra coisa importante de se saber é como se calcula o módulo de um vetor, a partir de suas componentes.
Novamente, se você lembrar que o vetor forma um triângulo com suas componentes, vai perceber que podemos usar o teorema de Pitágoras para encontrar o módulo do vetor:
Exemplo:
Explique o vetor abaixo e calcule o seu módulo:
Esse é um vetor de duas dimensões. Que aponta 20 unidades na direção de
O módulo é:
Soma e subtração entre vetores
Quando a gente têm as componentes dos vetores, então não tem segredo: é só somar ou subtrair as componentes iguais uma com a outra.
Exemplo: Some o vetor
Porém, as vezes nós não temos as componentes do vetor, mas temos o ângulo entre dois vetores. Nesses casos usamos a regra do paralelogramo
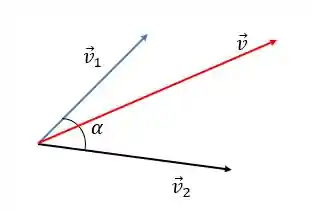
E se for uma subtração, então usamos:
Produtos entre vetores
Existem duas formas de multiplicar vetores. O Produto escalar e o produto vetorial
Produto escalar (
O produto escalar pode ser feito através do produto de termo a termo de cada vetor, dessa forma:
Mas se não temos as componentes do vetor, mas temos o ângulo entre dois vetores, podemos usar a fórmula:
Importante: O resultado desse produto é sempre uma grandeza escalar e não vetorial.
Produto vetorial (
O produto vetorial é um pouco mais complicado. Podemos calculá-lo através de um determinante:
Mas se não temos as componentes do vetor, mas temos o ângulo entre dois vetores, podemos usar a fórmula:
E para determinar a direção e sentido do vetor usamos a regra da mão direita.
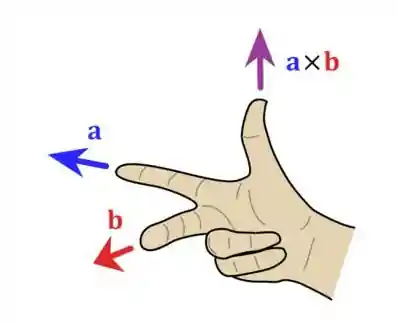
Videoaula
Quer saber mais sobre vetores? Então dá uma olhada nessa aula sobre o assunto:
Agora dá uma olhada aqui em baixo e vamos fazer uns exercícios 👇
Representando vetores matematicamente
Soma e subtração entre vetores
Produtos entre vetores
Videoaula
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Determine os ângulos feitos pelo vetor com o eixo positivo dos e dos .
Passo 1
Vamos, antes de mais nada, calcular a o módulo desse vetor:
Passo 2
Pra calcular os ângulos, a gente pode seguir o seguinte procedimento:
Calcular e , onde e são os ângulos que queremos achar, sabendo que:
Então, vamos ter que:
E a mesma coisa para :
Com os valores encontrados, vamos usar a função pra descobrir os ângulos.
Assim:
E:
Eiiiiii! Atenção aqui! Esse é um vetor no segundo quadrante (componente x negativa e componente y positiva). O valor que encontramos pra é o ângulo entre o eixo x positivo e o nosso vetor. Já o valor que encontramos pra é o ângulo entre o eixo y positivo e o nosso vetor.
Isso significa que se você subtrair um do outro TEM QUE DAR 90 GRAUS. Tendeu?
Observe que dividimos as componentes pelo módulo do vetor completo. Basicamente, é como se estivéssemos calculando o cosseno em um triângulo retângulo.
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 15. 1/4
Uma força é especificada pelo vetor . Calcule os ângulos entre e os eixos positivos
Passo 1
Primeiro, vamos calcular o módulo do vetor:
Passo 2
Assim:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 15. 1/2
Determine o valor da soma vetorial e do ângulo que faz com o eixo positivo . Complete tanto a solução gráfica quanto a algébrica.
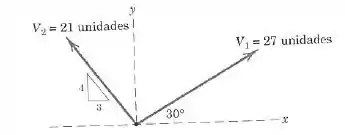
Passo 1
Pra resolver isso de forma algébrica, podemos escrever ambos os vetores em termos de suas componentes.
O vetor fica:
E quanto vale o ângulo que o vetor faz com positivo?
Bom, temos um triângulo semelhante ao triângulo formado pelo vetor e o eixo logo abaixo do mesmo na figura:
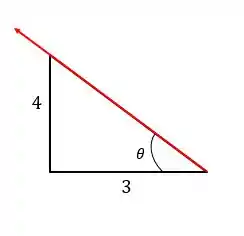
Tirando o arco tangente desse triângulo:
Opa, mas o vetor tá orientado no sentido contrário ao eixo, certo? Então devemos tomar o ângulo suplementar a esse ângulo, ou seja:
Assim:
Passo 2
E pra achar o vetor resultante? Bem, só somar componente a componente:
Passo 3
O vetor resultante faz um ângulo com
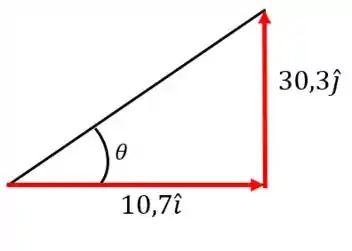
Pra achar esse ângulo, basta a gente tirar o arco tangente das componentes do vetor:
É como se tivéssemos tirado o arco tangente do triângulo formado pelas componentes:
Passo 4
Vamos resolver essa questão agora usando a regra do paralelogramo. Como sabemos os ângulos que cada vetor faz com o eixo , podemos descobrir o ângulo que um vetor faz com o outro, já que a soma de todos os ângulos deve ser igual a
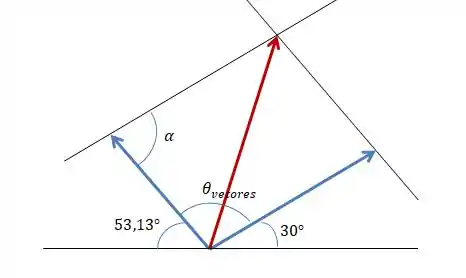
Assim:
Maaaass a gente precisa achar ... e já que num paralelogramo os ângulos opostos são iguais e somando todos dá 360°:
E agora sim vamos aplicar a lei dos cossenos pra achar a resultante:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 15. 1/3
Para os vetores e abaixo, determine o módulo da diferença vetorial e o ângulo que faz com o eixo positivo Complete tanto a solução gráfica quanto a algébrica.
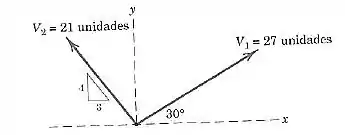
Passo 1
Escrevendo os vetores em termos de suas componentes, temos que:
E para o vetor , temos:
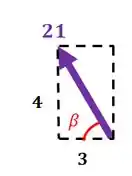
Então:
Pra resolver a questão algebricamente, vamos apenas subtrair componente a componente dos vetores:
Assim:
E:
E pra descobrir o ângulo que o vetor faz com o eixo , basta calcular o usando os valores das componentes:
Mas como queremos o correspondente desse ângulo no 2° quadrante, temos que achar o correspondente dele subtraindo de 180°. Então:
Passo 2
Antes de tudo, lembre-se que uma subtração de vetores é o equivalente a uma soma com um dos vetores com o sentido contrário (com o sinal de menos na frente):
Assim, os nossos vetores vão ficar assim ó:
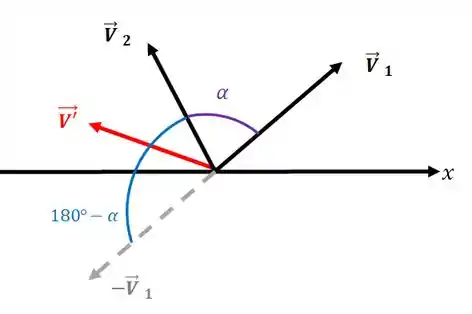
Perceba agora uma coisa: Antes, tínhamos um ângulo entre os vetores. Agora, o ângulo entre os vetores e tem que ser o complementar do antigo ângulo. Repare que o ângulo será:
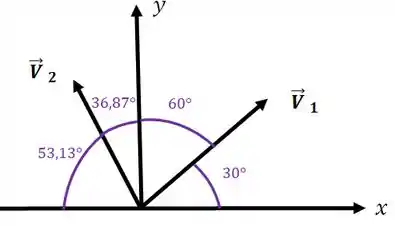
Então:
Assim, basta a gente aplicar a regra do paralelogramo:
Uma diferença pequena para o encontrado no outro método.
Resposta
Exercício Resolvido #5
Elaboração própria
Dados os vetores: , encontre o cosseno do ângulo entre os vetores.
Passo 1
O que podemos fazer é o seguinte:
Passo 2
O que podemos fazer, agora, é calcular o produto escalar e depois os módulos de cada vetor:
Assim:
Resposta
0,8
Exercício Resolvido #6
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987.
Se e é o ângulo entre , determinar
Passo 1
Vamos usar
Passo 2
Sabemos que:
Assim:
Resposta
Exercício Resolvido #7
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987.
Mostrar num gráfico um representante de cada um dos seguintes vetores:
Passo 1
Vamos usar a regra da mão direita pra resolver esse problema.
Mas antes, vamos localizas os nossos vetores unitários lembrando que os vetores e representam os vetores unitários dos eixos e, respectivamente.
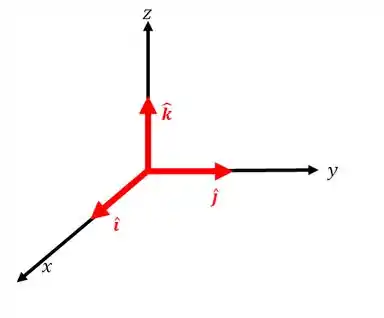
Passo 2
O primeiro produto vetorial é:
Então, vamos achar a direção através da regra da mão direita:
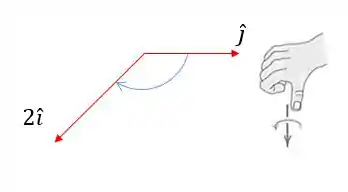
Logo, o vetor resultante é para baixo:
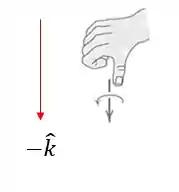
Assim:
E como achamos o módulo? O módulo do vetor vai ser a multiplicação dos módulos! Ou seja:
Ou então, basta lembrar que:
Só que estamos lidando apenas com vetores perpendiculares Assim:
Então, nessa questão, pra achar o módulo é só multiplicar os módulos de cada vetor!
Passo 3
Agora:
Então vamos fazer novamente a regra da mão direita
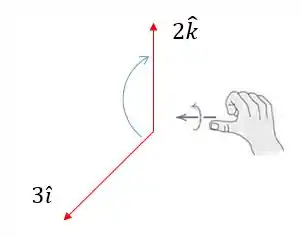
Logo, o sentido do vetor resultante será para a esquerda:
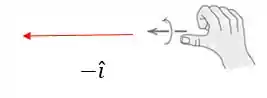
Como o módulo é a multiplicação de cada módulo anterior:
Vamos ter:
Resposta
Exercício Resolvido #8
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987.
Dados os vetores , calcular:
Passo 1
a)
Primeiro vamos realizar a soma dos vetores mias internos e depois vamos usar o produto vetorial com o determinante:
Passo 2
b)
Da mesma forma:
,
Resposta
a)
b)
Exercício Resolvido #9
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987.
Dados os pontos , determinar o valor de
Passo 1
Os vetores desse exercício são segmentos que ligam os pontos. Assim, para os gerar, devemos realizar as seguintes operações:
Passo 2
Agora basta a gente aplicar as operações:
Resposta
Exercício Resolvido #10
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987.
Dados os vetores e , determinar para que
Passo 1
Basta a gente aplicar:
Passo 2
Como o vetor resultante é nulo, todas as suas componentes são nulas:
Assim, da última e da segunda equação:
Passo 3
Para verificarmos se estamos corretos, vamos colocar os valores de e de na primeira equação!
Ótimo, então está correto!