Momentos em Três Dimensões
Produzido por Pablo RicardoTeoria
Introdução
Imagine um paralelogramo com uma força aplicada em um dos seus lados, assim:
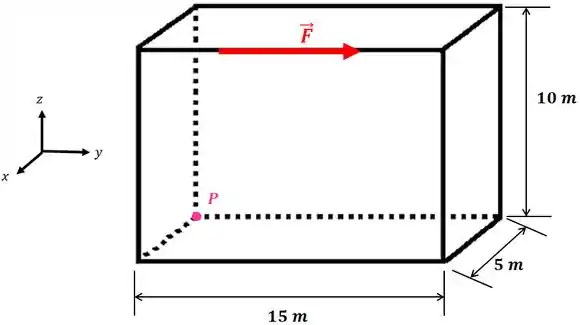
E queremos saber o momento no ponto . Como faremos isso?
Repare que agora temos um corpo com três dimensões... Então, quais das três distâncias têm que pegar para calcular o momento no ponto ?
Quando olhamos só para o eixo , a força está distante do ponto , mas quando olhamos para o eixo percebemos que a força está distante de . E aí?
É isso que vamos aprender agora, partiu?
Momento vetorial
Pra calcular o momento, basta a gente aplicar o produto vetorial que o representa:
Antes de tudo, você precisa descobrir duas coisas: quem é o vetor e quem é o vetor
Vamos pegar aquele exemplo inicial de novo:
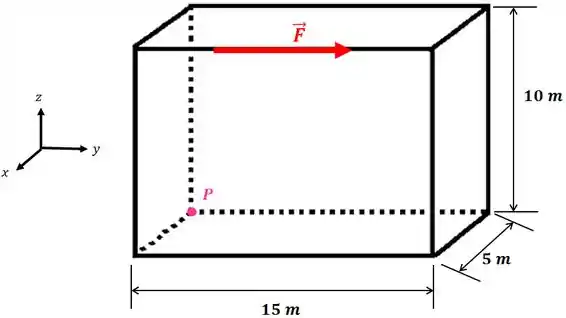
O vetor é o vetor posição que começa no ponto onde você quer calcular o momento (no nosso caso o ponto ) e termina em qualquer ponto da linha de atuação da força, assim:
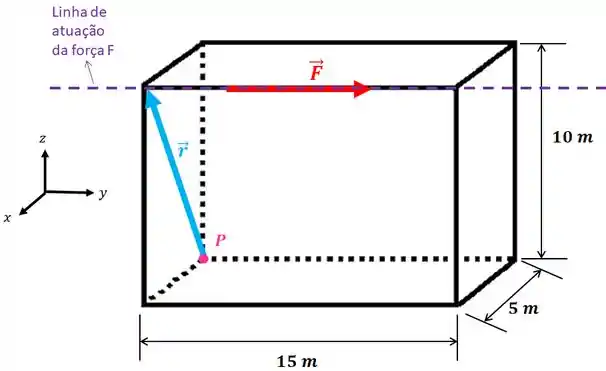
A linha de atuação da força é uma linha ao longo da direção da força , como podemos ver no desenho acima. Então, é muito mais fácil colocar o vetor na face do cubo do que chegando em outro ponto da linha de atuação, pois assim ele terá somente duas componentes: no eixo e , assim:
Se colocássemos o vetor terminando onde a força começa, a sua componente no eixo não seria mais zero o que daria mais trabalho nos cálculos! ![]()
A força está na direção do eixo , então vamos supor que seu módulo seja igual a , então:
Agora é só fazer este produto vetorial:
Teorema de Varignon em Três Dimensões
Se você achou o produto vetorial complicado, vou te mostrar outra maneira de calcular o momento! Vamos seguir esse passo a passo aqui:
- Primeira coisa que você tem que fazer é achar as componentes da força em cada eixo;
- Segundo passo é calcular o momento que cada componente faz com relação ao ponto e usar a regra da mão direita para saber o seu sentido;
- Agora é só somar todos os momentos para achar o momento total!
Mas a regra aqui é: para cada componente você vai pegar a distância perpendicular a ela e multiplicar pelo módulo da componente.
- Se a sua componente está no eixo , então você vai pegar as distâncias que estão nos eixos e , pois esses dois eixos são perpendicular ao eixo ;
- Se sua componente está no eixo , você vai pegar as distâncias que estão nos eixos e . Esse é o caso do nosso exemplo, olha:
- Se sua componente está no eixo , você vai pegar as distâncias que estão nos eixos e .
- Cálculo do momento para a distância que está no eixo : vamos olhar para a face da frente do retângulo, pois nela estão todas as informações que vamos usar:
- Cálculo do momento para a distância que está no eixo : vamos olhar para a face de cima do retângulo, pois nela estão todas as informações que vamos usar agora:
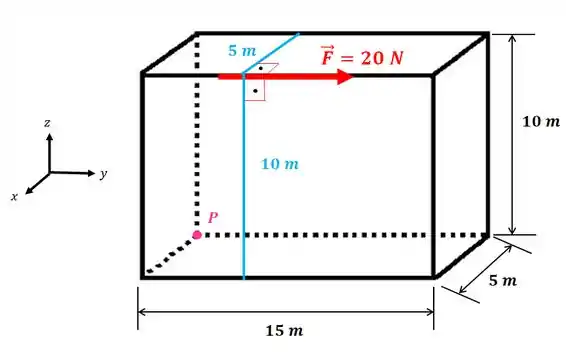
Repare que quando a força é paralela a um eixo, ela não gera momento em nenhum ponto que pertença a este eixo.
![]() Quando você utiliza esse método é preciso usar também a regra da mão direita.
Quando você utiliza esse método é preciso usar também a regra da mão direita.
Para entendermos melhor vamos usar o nosso exemplo:
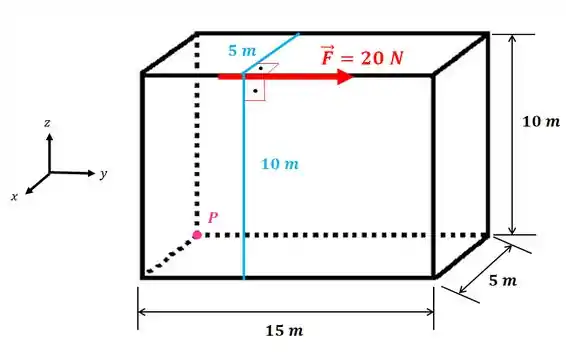
Já sabemos as duas distâncias que temos que pegar para calcular o momento com relação ao ponto . Agora vamos calcular cada momento e usar a regra da mão direita para cada um deles.
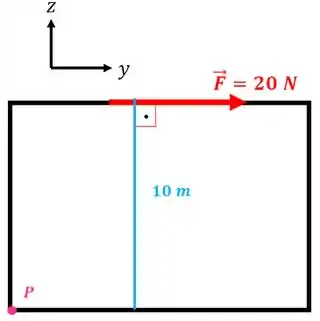
O módulo do momento vai ser:
Mas qual o sentido desse momento? E em que eixo ele está?
Essas perguntas são respondidas pela regra da mão direita: é só você colocar os 4 dedos da palma da sua mão direita (exceto o polegar) no sentido que a seta da força aponta e fazer sua mão girar em torno do ponto
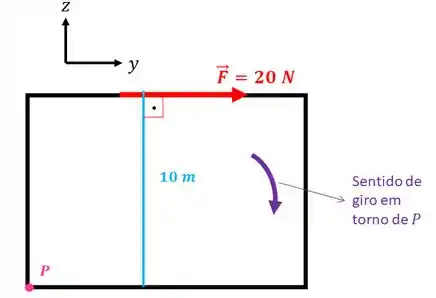
Repare que seu polegar aponta para dentro da tela, no sentido negativo do eixo . Então, o vetor momento no eixo será:
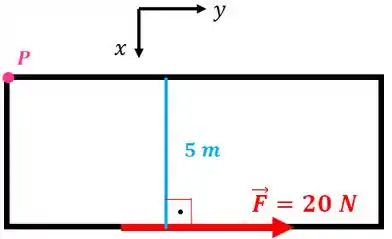
O módulo do momento vai ser:
Pela regra da mão direita você coloca os 4 dedos da palma da sua mão direita (exceto o polegar) no sentido que a seta da força aponta e fazer sua mão girar em torno do ponto :
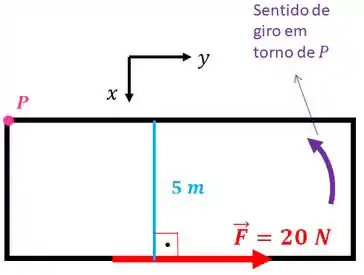
Repare que seu polegar aponta para fora da tela, no sentido positivo do eixo . Então, o vetor momento no eixo será:
Agora é só somarmos os dois momentos:
Repare que deu a mesma coisa do cálculo por produto vetorial, mas dessa maneira acabou dando mais trabalho!
Projeção de um momento em uma direção
Pode ser que a questão queira que você calcule o momento em relação a um certo eixo, ou direção. Vamos dizer que o objetivo seja calcular o momento em relação a uma direção. O que você fará, então?
Você vai projetar esse momento na direção , como fazíamos com as forças:
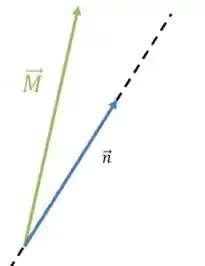
Show de bola? Só isso!
Ah, existe outra forma de se representar isso. Como podemos escrever o vetor momento assim:
Então:
A expressão é chamada de produto escalar triplo.
![]() Preste atenção em uma coisa: ali dentro tem dois produtos, um escalar e um vetorial. Você precisa fazer primeiro o vetorial, sempre!
Preste atenção em uma coisa: ali dentro tem dois produtos, um escalar e um vetorial. Você precisa fazer primeiro o vetorial, sempre!
Caso contrário, quando você fizer , será gerado um escalar e ele não poderá ser usado no produto vetorial com . Show?
Eu te aconselho, sinceramente, a primeiro calcular como já conhecemos e depois seguir com os cálculos do produto escalar. Isso te dará segurança e você não vai errar bobeira. Beleza?

É isso, bora fazer uns exercícios? ![]()
Teorema de Varignon em Três Dimensões
Projeção de um momento em uma direção
Exercícios Resolvidos
Exercício Resolvido #1
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2012, 61,2/117
Determine o momento da força em relação ao ponto .
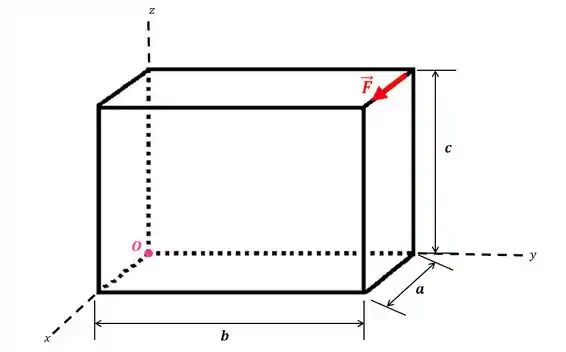
Passo 1
Vamos resolver essa questão usando o produto vetorial, porque os cálculos ficam muito mais simples.
Então, o nosso primeiro passo é determinar o vetor posição que começa no ponto e chega até qualquer ponto da linha de atuação da força:
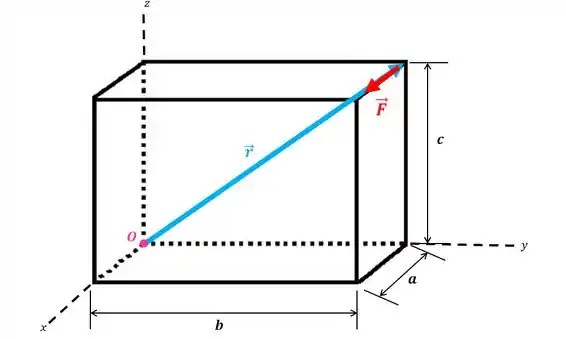
Então, o vetor posição será:
Passo 2
A força só tem componente no eixo e podemos escrever sua forma vetorial assim:
Pronto! Agora é só fazermos o produt vetorial:
Esse determinante fica:
Resposta
Exercício Resolvido #2
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 63,2/128
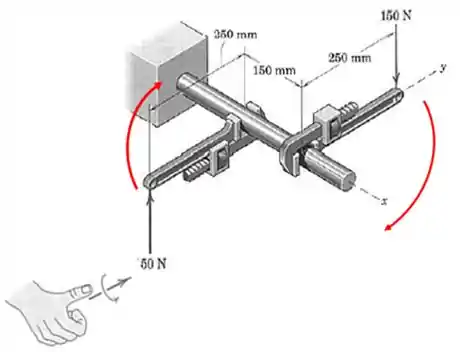
Um mecânico aplica a força horizontal de perpendicularmente à chave de boca, como indicado na figura. Determine o momento desta força em relação ao centro do parafuso em A linha do centro da chave está situada no plano
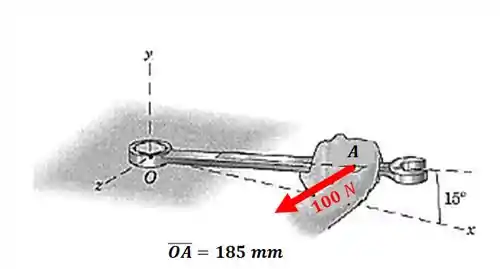
Passo 1
Vamos desenhar esse sistema sem os corpos:
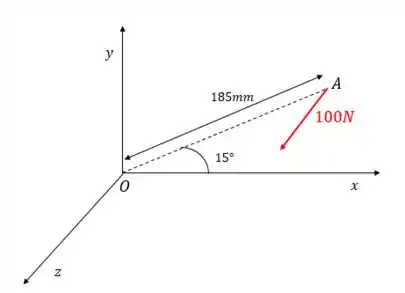
E definir primeiro o vetor :
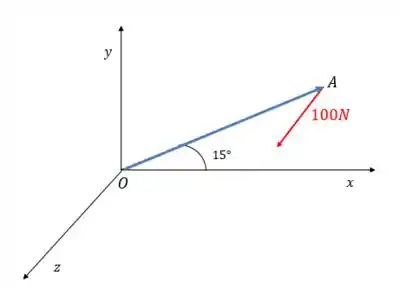
Como você pode ver, ele coincide com o segmento . Assim, podemos defini-lo em termos das projeções do segmento nos eixos:
A partir dessa figura podemos perceber que a projeção de no eixo vale :
E a projeção no eixo é:
Então, o vetor posição será esse carinha aqui:
Ou em metros:
Passo 2
Pelo enunciado, dá para ver que a força é paralela ao eixo e aponta no sentido positivo do mesmo. Sendo assim:
Então, vamos fazer o produto vetorial:
Teremos que:
O último determinante será nulo. Fazendo os dois determinantes, temos que:
Resposta
Exercício Resolvido #3
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 62,2/121
As duas forças que atuam nos cabos das chaves de grifo formam um binário Expresse o binário como um vetor.
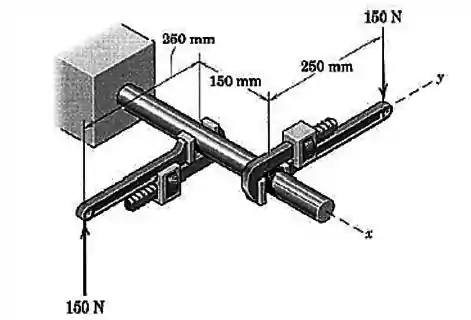
Passo 1
Nessa questão nós vamos fazer diferente: vamos dividir esse problema tridimensional em dois problemas bidimensionais.
Vamos chamar de e de os pontos onde cada força atua no sistema. Assim, visto de cima, temos:
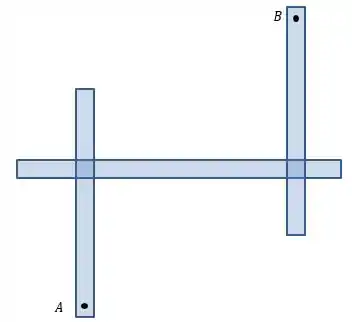
E visto de frente:
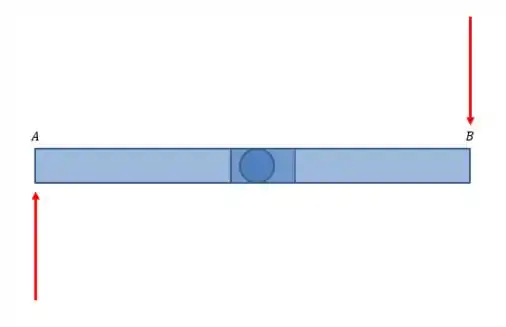
Show?
O que vamos fazer é o seguinte: calcular o módulo de cada uma das componentes do vetor momento total e depois definir o sentido e a direção dessas componentes usando a regra da mão direita.
Passo 2
Colocando os eixos e as distâncias na figura da vista de cima:
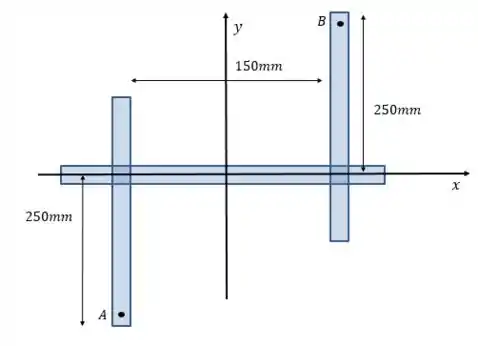
Não dá para ver as forças nessa vistas porque elas são perpendiculares à tela. Mas da figura do enunciado, você consegue saber que a força que atua em aponta para fora da tela e a que atua em atua para dentro.
Além disso, a distância entre as forças é de , assim, o binário é dado por:
Qual a direção desse vetor momento? Bora usar a regra da mão direita:
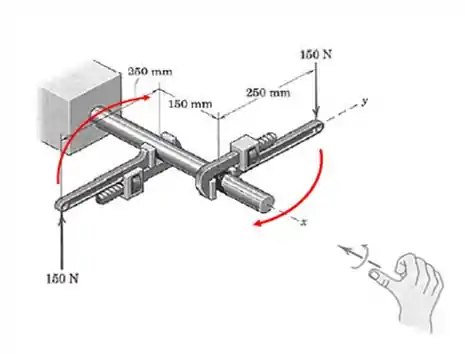
Pela regra, o vetor aponta na direção negativa de . Assim:
Bora calcular a outra componente.
Passo 3
Fazendo a mesma coisa de antes, mas agora com relação ao eixo :
Repare que uma das forças não tem braço de alavanca com relação ao eixo , então o seu momento é nulo.
E pra determinar o sentido? Regra da mão direita:
Dá pra ver que essa componente aponta na direção positiva de , né? Assim:
Passo 4
O vetor momento binário será dado por:
Resposta
Exercício Resolvido #4
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 62,2/123
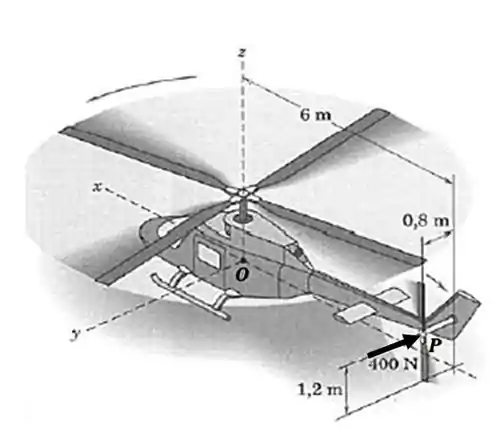
Um helicóptero está mostrado e são dadas certas coordenadas tridimensionais. Durante um teste no solo, uma força aerodinâmica de é aplicada ao rotor de cauda , como mostrado. Determine o momento desta força em relação ao ponto da fuselagem.
Passo 1
Vamos desenhar esse sistema sem o helicóptero, afinal de contas ele atrapalha um pouquinho a nossa visualização, né?
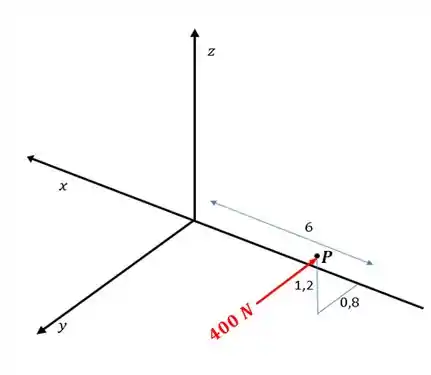
Ou seja, a força está sendo aplicada no ponto:
Então, o vetor distância do ponto até o ponto é dado por:
E a força? Bom, pelo desenho do enunciado, a força é paralela ao eixo , no sentido negativo do mesmo. Então, teremos esse carinha aqui:
Passo 2
Show de bola! Temos tudo para calcular o nosso momento:
Então, vamos ter que:
O determinante do centro, que tem como unitário o , vai ser nulo, assim:
Sacou? É aquele mesmo passo a passo de sempre: define o vetor , depois define o vetor e, por fim, joga no determinante do produto vetorial.
Resposta
Exercício Resolvido #5
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 62,2/122
A barra curva tem uma massa por unidade de comprimento. Determine o momento do peso da barra em relação ao ponto
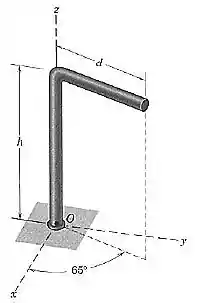
Passo 1
Vamos aplicar o momento calculado de forma vetorial nesse problema.
Primeiro, vamos dividir a estrutura em duas barras: uma barra vertical de comprimento e outra barra horizontal de comprimento . A força peso de cada uma dessas barras será:
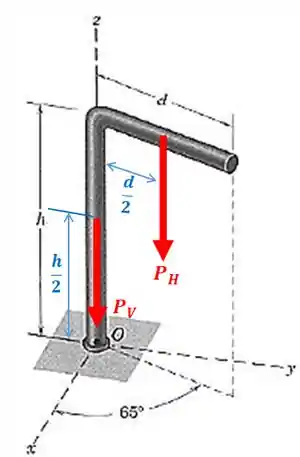
Onde, é o peso da barra horizontal e é o peso da barra vertical.
Perceba que o peso sempre aponta pra baixo, ou seja, na direção negativa de
Sendo assim, o peso da barra vertical não exerce momento com relação ao ponto , já que a linha de ação do peso desta barra intercepta o ponto
Dessa forma, só a parte horizontal da barra exercerá momento. Essa parte tem o peso dado por:
Passo 2
Agora vamos definir o vetor :
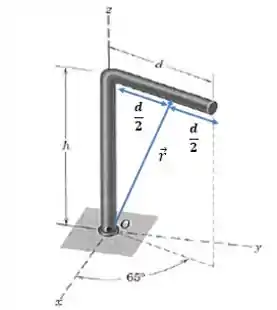
Pela figura, as componentes de são:
Passo 3
O momento será dado por:
Então:
Repare que o último determinante, o que está acompanhado de , é nulo. Calculando os outros:
Arrumando isso e substituindo o valor do cosseno e do seno de
Resposta
Exercício Resolvido #6
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 62,2/124
A força de está aplicada ao ponto do conjunto de suportes. Determine o momento dessa força em relação ao ponto
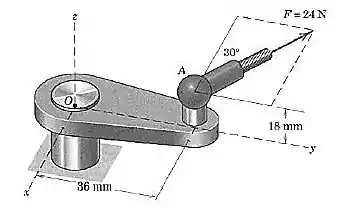
Passo 1
Vamos desenhar o sistema sem os corpos:
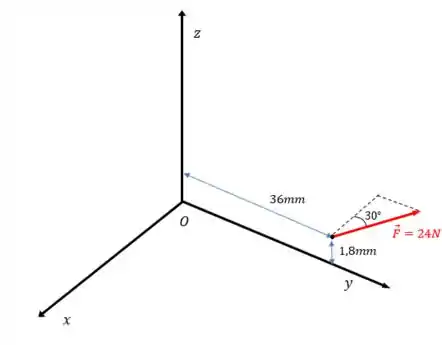
Passo 2
De acordo com a figura, podemos definir o vetor por:
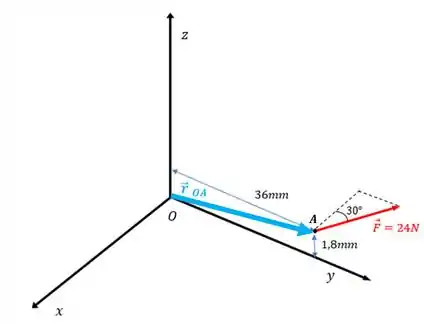
Agora precisamos definir a força. Pela figura, a força faz um ângulo de com o sentido negativo do eixo
Assim:
Passo 3
Agora, pra calcular o momento, vamos usar o nosso velho amigo produto vetorial:
Desenvolvendo:
Resposta
Exercício Resolvido #7
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 61,2/118
Determine o momento da força em relação ao ponto
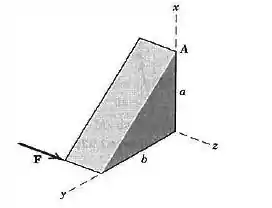
Passo 1
Vamos primeiro escrever o vetor
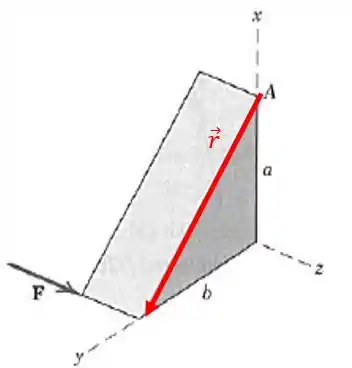
O vetor pode ser escrito como a diferença entre um ponto inicial e um final, sendo esses:
Assim:
Passo 2
E a força ? Pela figura, dá pra perceber que ela é paralela ao eixo e aponta no sentido positivo do mesmo. Sendo assim:
Passo 3
Agora vamos escrever o nosso produto vetorial que representa o momento:
Vamos ter que:
Resposta
Exercício Resolvido #8
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 62,2/126
Determine o momento associado ao par de forças de aplicado à estrutura em
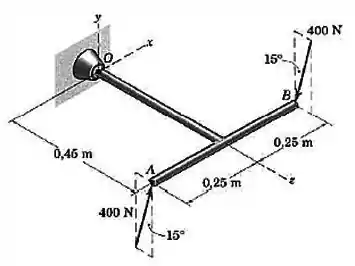
Passo 1
Nós vamos resolver essa questão da seguinte forma: calculando o momento de cada uma das forças e depois somando:
Passo 2
O momento é em relação ao ponto médio da placa. Desta forma, precisamos calcular os vetores posição e :
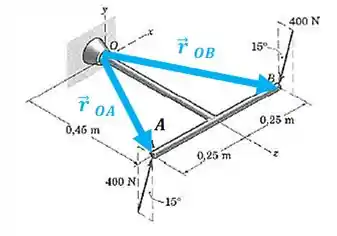
Então, para o vetor posição , vamos ter:
E para o vetor posição , vamos ter:
Agora só falta definir as forças. Olhando pra figura, vemos que o ângulo que as forças fazem com o eixo é de . Assim:
Passo 3
Assim, os momentos são calculados segundo os seguintes produtos vetoriais:
Então, para :
Para :
Portanto:
Resposta
Exercício Resolvido #9
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 62,2/125
O tubo em ângulo reto é visto abaixo. Substitua a força trativa de que o cabo exerce no ponto por um sistema força binário no ponto
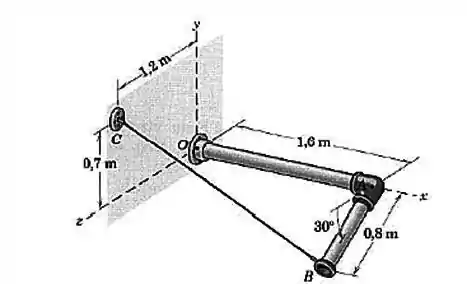
Passo 1
Bom, sabemos que a força atua no ponto através da reta que une .
Além disso, como a força é trativa, o vetor da força terá o sentido indo de para
Como já fizemos antes, o vetor que representa é dado por:
Observando a figura, vemos que:
Se liga: os eixos não estão colocados nos lugares de costume.
Já o ponto é um pouquinho mais complicado pois vamos ter que trabalhar com seno e cosseno. Dá uma olhada: o comprimento faz um ângulo de com a horizontal.
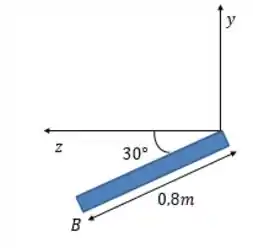
Sendo que a coordenada disso daí é . Então:
Passo 2
Assim:
Passo 3
Então:
Passo 4
Assim, a força é dada por:
Passo 5
Vamos calcular o momento que essa força exerce em . Usando a distância
Assim, o momento será dado por:
Passo 6
Beleza, calculando a força resultante e o momento da força em relação a , você já tem o binário.
O sistema força binário é formado por:
Resposta
Exercício Resolvido #10
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 63,2/132
Ao levantar uma carga da posição , desenvolve-se no cabo uma força trativa de Calcule o momento que produz em relação à base da grua de construção.
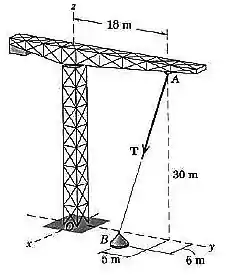
Passo 1
Vamos desenhar o sistema sem os corpos:
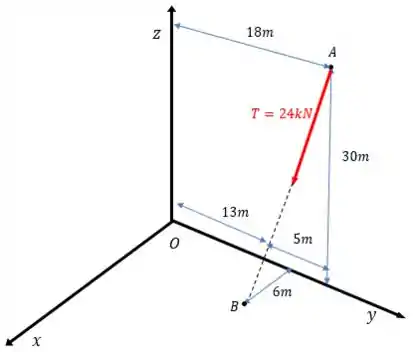
Passo 2
Pra definir , vamos antes definir o vetor normalizado que representa a direção O ponto tem as coordenadas:
E o ponto está em:
Então, o vetor que representa a direção é:
Normalizando:
Para achar o vetor é só multiplicar o seu módulo pelo vetor unitário, assim:
Passo 3
Agora vamos achar o vetor
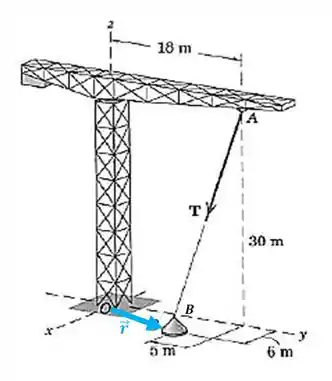
Passo 4
Assim:
Assim:
Resposta
Exercício Resolvido #11
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 64,2/134
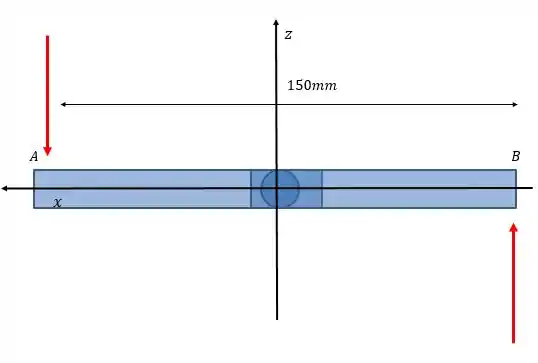
Para reduzir o momento indesejável em relação ao eixo , um mecânico usa sua mão esquerda para sustentar o cabo da chave no ponto . Que força direcionada para cima, , deve ser exercida para que não haja momento em relação ao eixo ? Qual é, então, o momento resultante em relação a
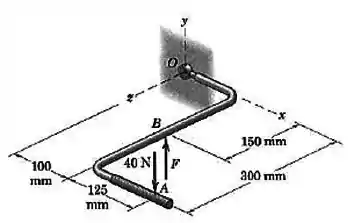
Passo 1
Podemos resolver esse problema dividindo-o em problemas bidimensionais.
A primeira coisa que precisamos descobrir é qual é a força necessária que deve ser aplicada em para que não haja momento em relação a . Ou seja:
Vamos desenhar o esquema das forças nesse caso, baseando-se no nosso enunciado é:
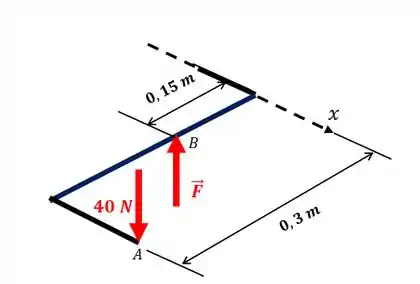
Pronto! Desenhamos o que nos interessa.
Perceba que cada força produzirá um momento em sentido contrário ao outro. Sendo que a força de produz um momento no sentido positivo do eixo , pela regra da mão direita. E o força , que queremos saber, produz um momento negativo:
Pronto, matamos metade da questão.
Passo 2
Agora queremos saber o momento resultante em relação a .
Em primeiro lugar: não existe momento em relação ao eixo , já que as forças são paralelas a esse eixo. Também vimos que o momento resultante em relação a é nulo, então nos resta saber o momento em relação ao eixo
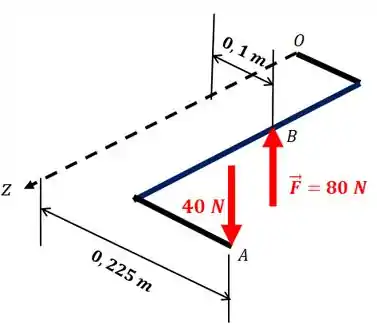
Pela figura, o sentido anti-horário é o positivo. Então, o módulo do momento em é:
Escrevendo de forma vetorial:
Ou:
Resposta
Exercício Resolvido #12
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 64,2/135
Determine o momento da força de em relação ao ponto
- Usando a relação do produto vetorial.
- Projetando a força em seus componentes e achando os seus respectivos momentos.
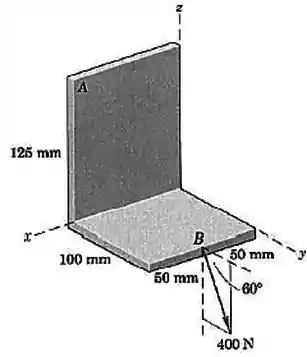
Passo 1
De forma vetorial:
Primeiro, vamos definir o vetor .
Passo 2
Agora vamos definir a força:
Feito isso, podemos calcular o produto vetorial:
Assim:
Passo 3
Para fazer o próximo item, vamos primeiro calcular as componentes da força:
Passo 4
Vamos analisar cada eixo e ver quais forças exercem momento em cada um desses:
Eixo
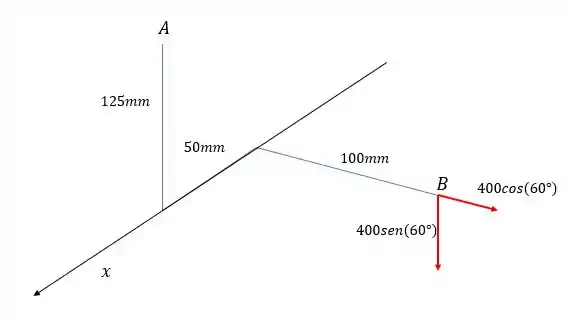
A força de faz um momento no sentido horário, já a outra componente um momento no sentido anti-horário. Tomando o sentido anti-horário como positivo, vamos ter que:
Escrevendo vetorialmente:
Vamos checar se esse sentido é o certo? Bom, o momento é horário, já que é negativo:
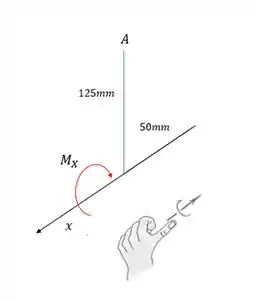
Pela regra da mão direita, o sentido é realmente negativo em Então escrevemos certo!!!
Passo 5
Eixo
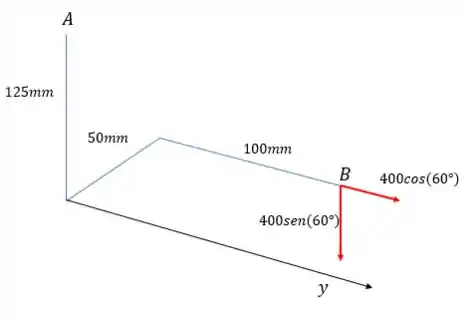
Nesse caso, só a componente vertical realiza momento, pois a componente horizontal é paralela ao eixo . Assim:
E o sentido? Bom, dá para ver que o sentido de rotação, nesse caso, é o horário. Sendo assim, usando a regra da mão direita:
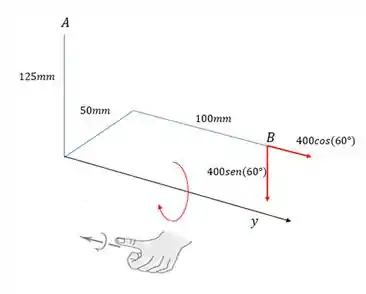
Assim, o sentido do vetor momento é contrário ao sentido positivo do eixo , então:
Passo 6
Eixo :
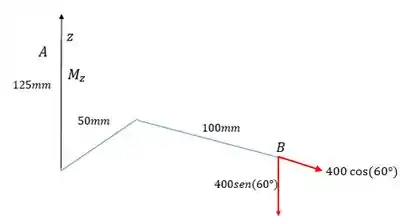
Em relação ao eixo , só a força horizontal exerce momento, pois a força vertical é paralela ao eixo . O momento é nesse sentido aqui:
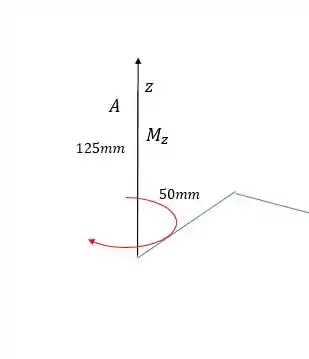
Assim:
Para ver o sentido, vamos usar a regra da mão direita:
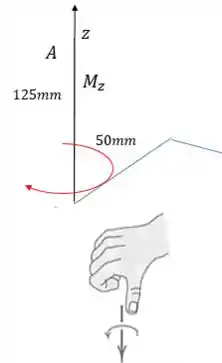
Assim, o vetor momento aponta no sentido negativo de . Então:
E por fim:
Resposta
Exercício Resolvido #13
J.L. Meriam & L.G. Kraige, Mecânica para engenharia, Estática, 6° ed. RJ: LTC, 2009, 65,2/141
Uma força vertical de é aplicada à manete do mecanismo de abertura de janelas quando a manivela está na horizontal. Determine o momento da força em relação ao ponto e em relação à linha .
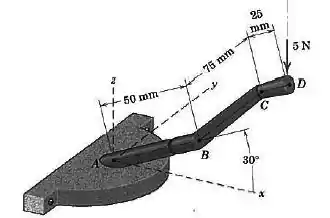
Passo 1
Vamos primeiro calcular o momento em relação ao ponto . Para isso, como de costume, vamos desenhar o sistema sem esses corpos:
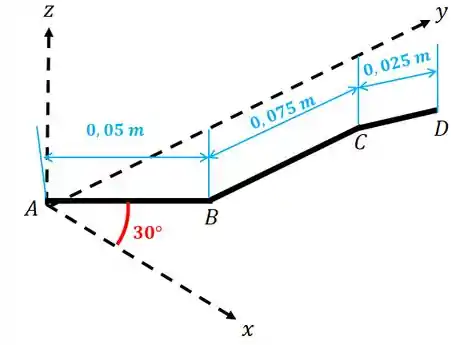
Perceba uma coisa: o trecho é paralelo ao eixo e aponta para dentro da tela. Note também que a força é paralela ao eixo e aponta no sentido negativo do mesmo:
Vamos escrever o vetor .
Mas esse trecho é todo torto, concorda? De até ele é de um jeito, de até de outro e de até de outro.
Podemos, então, escrever como uma soma de três vetores posição:
Para encontrar as componentes de , apenas use cosseno e o seno pra calcular as componentes e
O trecho , pelo contrário, só tem uma componente positiva que aponta na direção positiva de
E o trecho você faz que nem o . Esse trecho possui a mesma inclinação que o trecho
Somando os vetores:
Somando as componentes:
Passo 2
Tudo pronto para calcularmos o nosso momento:
Expandindo:
Perceba que o último determinante dá zero. Calculando os outros:
Passo 3
Show de bola. Agora queremos saber o valor desse momento em relação à linha
O que isso significa? Ah, isso nada mais é do que a projeção do momento naquela direção: a direção
Assim, calcularemos:
Ou seja, o produto escalar entre o momento e o vetor normalizado da direção , que nos dá o módulo da projeção, vezes o próprio vetor .
No final das contas, isso dada mais é do que o nosso produto:
Então, vamos ter que calcular esse vetor .
Passo 4
Não se preocupe, é fácil achar esse . Isso porque já calculamos antes o , então é só normalizar ele:
O módulo deste vetor é:
Então, o vetor unitário vai ser:
Passo 5
Show de bola! Já sabemos que , então:
Vamos escrever esse produto de uma maneira mais fácil de visualizar o que está acontecendo. Algumas componentes ali são nulas, e só podemos fazer o produto termo a termo e entre termos iguais:
Agora que temos que sabemos que:
Podemos escrever este momento como um vetor multiplicando seu módulo pelo vetor unitário: