A chave especial mostrada é usada para parafusos de difícil acesso que tem uma especificação de baixo torque. Determine o momento da força de aplicada no ponto do cabo da chave em relação a . Discuta qualquer desvantagem dessa chave.
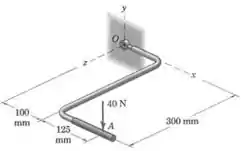
Passo 1
Vamos pensar na definição de momento de uma força:
Podemos desenhar esses vetores na figura:
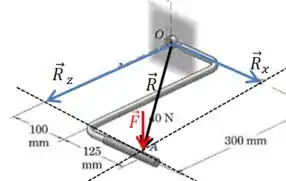
E agora é interessante reescrever a equação do momento da seguinte forma:
Passo 2
Como os três vetores já são perpendiculares fica fácil caclcular o produto vetorial. A regra da mão direita dá a direção de cada um dos vetores momento.
E então o momento total é:
Ou:
Passo 3
Agora podemos discutir as desvantagens dessa chave.
O momento em torno do eixo indica uma tendência à rotação no plano , o que não é um problema, como podemos ver pela figura, porque há espaço para essa rotação.
Já o momento (ainda maior) em torno do eixo , que indica uma tendência à rotação no plano , é um problema, pois pode “forçar” o suporte ao favorecer a rotação em um sentido “contra a parede”.
Resposta
O momento total em relação a é .