Concentradores de Tensões em Flexão
Teoria
Nos assuntos anteriores, você pode já ter visto como lidar com concentradores de tensões em casos de carga axial e torção.
Se sim, eu tenho uma boa notícia!
Os concentradores de tensões em flexão funcionam da mesma forma que funcionavam nesses casos anteriores.
Isto é, para descobrir as tensões máximas que ocorrem em um concentrador de tensões, você deve:
- Identificar a seção crítica na região do concentrador (normalmente a seção menor);
- Calcular as tensões para essa seção;
- E, em seguida, multiplicar essas tensões por um coeficiente , retirado de um gráfico.
Agora, caso você ainda não tenha visto como lidar com concentradores de tensões...
Estamos aqui agora para aprender!
Introdução
Vamos dizer que você têm a placa de espessura abaixo, submetida a um certo momento fletor :
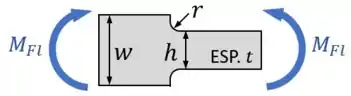
Nessa placa, nós temos:
- Uma seção inicial/maior de altura ;
- Uma seção final/menor de algura ;
- Uma redução rápida de seção entre essas seções, de acordo com o adoçamento de raio .
- E um momento fletor aplicado, que vai gerar na placa tensões de flexão de acordo com a fórmula da flexão:
Mas aí...
Em reduções rápidas de seção como essa, ocorre um efeito chamado de concentração de tensões, que aumenta o valor das tensões nessas regiões:
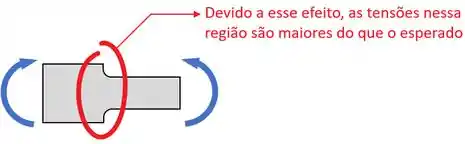
Então...
Se a gente precisar calcular a tensão de flexão máxima nessa placa...
Como a gente faz?
Seção Crítica
A primeira coisa que podemos observar é que as tensões nessa placa são maiores na seção menor, de altura .
Como assim?
Se olharmos para a fórmula da flexão:
...podemos ver como para um mesmo momento fletor , o que determina se a intensidade da tensão é maior ou menor é o termo “”.
Avaliando esse termo para ambas as seções dessa peça:
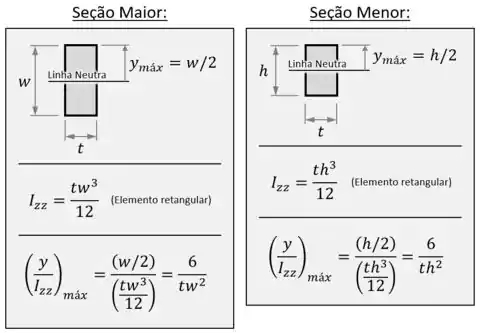
...vemos que ele atinge um valor máximo para a seção maior e um valor máximo para a seção menor.
E como , temos que:
O que significa que o termo “” (e consequentemente a tensão ) atinge valores maiores para a seção menor, de altura .
Assim, confirmamos que, para essa região de concentração de tensões que estamos estudando, a seção crítica (aquela em que as tensões são maiores) é a seção menor.
Repare que aqui nós não calculamos o módulo de seção. Apenas fizemos uma análise para determinar qual é a seção crítica.
Coeficiente de Concentração de Tensões
Agora, simplesmente aplicar a fórmula da flexão para essa seção crítica não é o suficiente para determinar a tensão máxima nessa placa.
Isso porque por causa do efeito da concentração de tensões, as tensões nas regiões afetadas por esse efeito são multiplicadas por um coeficiente .
Esse coeficiente é chamado de coeficiente de concentração de tensões e é determinado através de gráficos específicos para cada geometria de peça.
Para uma peça como a placa acima, por exemplo, esse gráfico é assim:
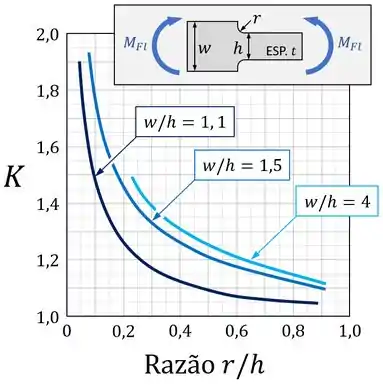
Daí que, para determinar o valor de usando esse gráfico, devemos:
1. Identificar na peça os valores das dimensões indicadas no desenho que acompanha o gráfico;
Nesse caso, devemos identificar os valores de “”, “” e “”, conforme o desenho no canto superior do gráfico:
2. Escolher qual curva do gráfico devemos usar;
Nesse caso, para escolher essa curva, devemos calcular a razão “” e escolher a curva correspondente:
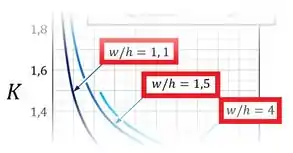
E, finalmente:
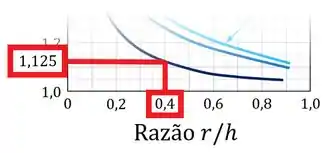
3. Calcular a razão indicada no eixo horizontal do gráfico e encontrar o valor correspondente de , tendo em mente a curva escolhida no passo anterior.
Como mostra a imagem abaixo, onde encontrou-se que :
Fórmula da Flexão com Concentração de Tensões
Então, tendo em mente tudo o que vimos, concluímos que:
Para calcular as tensões de flexão máximas em uma região com concentração de tensões, basta usar a fórmula da flexão multiplicada pelo coeficiente retirado do gráfico:
...lembrando sempre de aplicar essa fórmula para a seção em que as tensões vão ser maiores, ou seja, a seção crítica.
Sendo que, na prática dos exercícios que vemos em resistência dos materiais, a seção crítica de uma região com concentração de tensões vai ser sempre a seção menor.
Para revisar tudo que vimos, vamos considerar outro exemplo:
Outro tipo de concentrador de tensões comum são as ranhuras em uma placa, como na imagem abaixo:
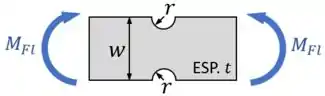
Daí que, para calcular as tensões de flexão máximas nessa placa, basta aplicar a fórmula:
...para a seção crítica, que nesse caso vai ser a seção mais reduzida devido às ranhuras de raio :
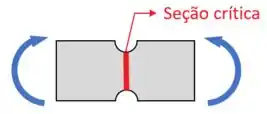
Sendo que para encontrar o valor do coeficiente , devemos observar o gráfico do coeficiente fornecido pelo exercício ou pelo livro para casos de uma placa com ranhura.
E pronto!
Aí, se você quiser ver um exercício desses na prática, é só seguir para os exercícios resolvidos:
Seção Crítica
Coeficiente de Concentração de Tensões
Fórmula da Flexão com Concentração de Tensões
Exercícios Resolvidos
Exercício Resolvido #1
Ferdinand P. Beer et al., Mecânica dos materiais, 5ª ed. Porto Alegre: AMGH, 2011, pp. 254 & 262-4.64.
Ranhuras semicirculares de raio devem ser fresadas nos lados de uma barra de aço, conforme mostra a figura. Usando uma tensão admissível de , determine o maior momento fletor que pode ser aplicado ao elemento quando o raio das ranhuras semicirculares for e .
Para determinação do coeficiente de concentração de tensões , utilize o gráfico abaixo:
Passo 1
O que está acontecendo?
Devido ao momento fletor aplicado na peça da figura, vão surgir nas seções transversais dessa peça tensões de flexão de acordo com a fórmula da flexão:
Onde:
- (ou ) é o momento fletor na seção;
- é a posição do ponto em que se quer avaliar a tensão em relação à linha neutra da seção;
- & (ou ) é o momento de inércia da área da seção,
Agora...
Nesse caso do exercício, como todas as seções transversais dessa peça são retangulares, vamos ter que:
1. A linha neutra das seções dessa peça ficam bem no meio das seções:
Dessa forma, os valores máximos da posição em relação à linha neutra (que implicam nos valores máximos da tensão ) são .
& 2. O momento de inércia da área das seções dessa peça vai ser dado pela fórmula:
Isso significa que a tensão máxima em uma seção dessa peça vai ser:
O que dá:
Ou, em módulo:
Daí que, vendo a nossa peça:
...vemos que as suas seções tem uma base e que tensão máxima na peça vai ocorrer para a seção com as ranhuras semicirculares, onde a altura vai ser:
O que é menor que a altura de das demais seções.
Agora, além disso...
Na seção das ranhuras nós ainda vamos ter um fator de concentração de tensões devido à mudança drástica de seção transversal causada pelas ranhuras.
Por causa desse fator, a tensão máxima na seção das ranhuras (que já é a seção de tensão máxima) deve ser multiplicada por um coeficiente de concentração de tensões .
Ou seja, para a nossa peça:
E o que é que o exercício quer?
Ele quer saber o momento fletor máximo que pode ser aplicado nessa peça de tal forma que as tensões na peça não superem a tensão admissível .
Ou seja, ele quer saber o momento fletor máximo que ainda satisfaz a condição:
Daí que, substituindo a expressão que acabamos de encontrar para :
...e isolando , vamos encontrar que esse momento fletor máximo vai ser dado por:
Aí, no item , o exercício quer que a gente determine esse momento fletor máximo considerando que as ranhuras tem um raio enquanto que no item devemos considerar .
Então, para resolver o exercício...
Devemos definir, para cada caso ( e ):
- A altura da seção transversal menor da peça;
- & o coeficiente de concentração de tensões , que pode ser obtido através do gráfico fornecido.
Feito isso, poderemos aplicar a fórmula que desenvolvemos acima:
...para cada situação, determinando assim o momento fletor máximo em cada caso, resolvendo o exercício.
Passo 2
Então vamos lá!
Começando pelo item :
Considerando que as ranhuras tem um raio , a seção menor da peça vai ter uma altura :
Definida essa altura, podemos definir em seguida o coeficiente de concentração de tensões para esse caso.
Para tanto, devemos olhar para o gráfico fornecido:
Olhando para o gráfico, vemos que temos que definir as razões e .
Daí que, olhando para o desenho em miniatura no canto do gráfico:
E comparando esse desenho com a nossa peça, identificamos que , e .
Dessa forma, conseguimos definir as razões:
Aí, inserindo esses valores no gráfico:
...encontramos que:
Passo 3
Agora que já definimos a altura e o coeficiente de concentração de tensões para o item , já podemos calcular o momento fletor máximo para esse item.
Aplicando a fórmula que desenvolvemos no passo , temos:
Substituindo:
- ;
- ;
- ;
- & ,
- ;
- ;
- ;
- & ,
Encontramos que:
Reescrevendo esse resultado em , temos:
O que significa que o momento fletor máximo permitido no caso em que é , que é a resposta do item .
Passo 4
Seguindo para o item :
Considerando que as ranhuras tem um raio , a seção menor da peça vai ter uma altura :
Em seguida, comparando com a nossa peça as dimensões indicadas no canto do gráfico de :
...encontramos que, no caso do item , , e .
Dessa forma, as razões e ficam assim:
Aí, inserindo os valores dessas razões no gráfico do coeficiente de concentração de tensões , de forma análoga ao que fizemos no passo , vamos encontrar que:
Passo 5
Por fim, só falta definir o momento fletor máximo para o item .
Aplicando a fórmula que desenvolvemos no passo , temos:
Substituindo:
Encontramos que:
Reescrevendo esse resultado em , temos:
O que significa que o momento fletor máximo permitido no caso em que é , que é a resposta do item .
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 243-6.150.
Determine o comprimento da porção da barra de modo que as tensões de flexão máximas em , e sejam as mesmas. A barra tem espessura de .
Para a determinação do coeficiente de concentração de tensões , utilize o gráfico abaixo:
Passo 1
O que está acontecendo?
Devido à carga aplicada na barra da figura, vão surgir esforços internos nela na forma de forças cortantes e momentos fletores .
Esses momentos fletores vão gerar tensões normais de flexão nas seções transversais da barra, de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento na seção;
- é a posição do ponto da seção em que se quer avaliar a tensão em relação à linha neutra de seção;
- & (ou só “”) é o momento de inércia da área da seção.
Sendo que aqui, como essa barra tem seções transversais sempre retangulares, vamos ter que:
1. O momento de inércia da área dessas seções vai ser dado pela fórmula:
Onde é a base da seção, igual à espessura de da barra para qualquer seção e é a altura da seção, igual à para as seções e e igual à para a seção .
(Dessa forma, temos que o momentos de inércia da área das seções e são iguais.)
& 2. As tensões máximas nessas seções vão ocorrer nas bordas superiores e inferiores das seções, onde :
Além disso...
Nas seções e , devido à mudança brusca no tamanho da seção transversal, haverá uma concentração de tensões de acordo com um coeficiente , de tal forma que a tensão nessas seções vai ser dada por:
Sendo que o valor de pode ser encontrando utilizando o gráfico fornecido.
E, por fim...
Ainda temos que, como a carga é a única carga externa na barra e está centralizada entre os dois apoios na barra, os esforços externos e internos nessa barra vão ser simétricos.
Dessa forma, vamos ter que o momento fletor nos pontos e vão ser iguais.
E o que é que o exercício quer?
Ele quer saber qual deve ser o comprimento indicado na figura para que as tensões de flexão máximas no ponto , que ocorrem nos pontos :
Seja igual às tensões de flexão máximas nos pontos e , que ocorrem nos pontos , e onde há uma concentração de tensões
Então, para resolver o exercício…
Temos que:
1. Aplicar os métodos da estática (DCL, equilíbrio, análise dos esforços internos) para descobrir os momentos fletores em e (que vão ser iguais) e em , em função do comprimento ;
2. Determinar o coeficiente de concentração de tensões nos pontos e ;
& 3. Igualar as tensões máximas e acima e isolar o comprimento , descobrindo assim qual o valor desse comprimento para que essas tensões sejam iguais.
Passo 2
Então vamos começar fazendo o diagrama de corpo livre ou “DCL” da peça!
Nela, temos:
- No ponto “” na extremidade esquerda da barra, um apoio móvel que vai realizar uma reação na vertical ;
- E no ponto “” na extremidade direita, um apoio fixo que vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
Dessa forma, o nosso DCL fica assim:
Passo 3
Feito o DCL, podemos aplicar o equilíbrio na peça.
Aplicando o somatório de forças na vertical, temos:
O que significa que:
E aplicando o somatório de momentos em relação ao ponto , temos:
Dividindo tudo por e isolando , encontramos que:
Aí, substituindo essa relação que encontramos na expressão anterior , encontramos que:
O que significa que:
E, como , isso significa que:
E assim terminamos de determinar todos os esforços externos na nossa peça.
Passo 4
Em seguida, fazemos uma análise dos esforços internos.
Aqui, nosso objetivo é descobrir os momentos fletores em , e .
Mas como já sabemos que o momento fletor em é igual ao em , só precisamos determinar os momentos fletores em e em .
Dessa forma, sabendo que as mudanças na seção transversal não afetam os esforços internos, é suficiente observar os esforços internos somente nas seções entre e :
...para determinarmos os momentos fletores em e em .
Aí, aplicando o equilíbrio de momentos para o desenho acima em relação ao ponto da seção, temos:
Substituindo e isolando , encontramos que:
Aí, como para o ponto , , temos que:
E como para o ponto , , temos:
Passo 5
Agora, antes de prosseguir com a resolução do exercício, precisamos determinar o coeficiente de concentração de tensões em e .
Então vamos olhar para o gráfico de :
Comparando as medidas indicadas no esquema no topo dessa gráfico com as medidas indicadas na figura original do exercício, vemos que , e .
Assim, podemos calcular as razões:
Aí, escolhendo a curva para e inserindo o valor da razão no gráfico acima, encontramos que:
Passo 6
Agora que já:
- Usamos o que precisávamos dos métodos da estática para determinar os momentos fletores em e , e em , ;
- E determinamos o coeficiente de concentração de tensões em e ,
...podemos seguir para a próxima etapa do exercício.
O exercício quer saber qual o comprimento para o qual as tensões máximas em , e são iguais.
Então vamos igualar essas tensões:
Aplicando a fórmula da flexão para a determinação das tensões máximas nesses pontos, e lembrando da concentração de tensões nos pontos e , vamos ter que:
Simplificando, isso fica assim:
Aplicando a formula do momento de inércia da área de um elemento retangular para cada seção, vamos ter:
Simplificando tudo que é possível simplificar, temos:
Em seguida, substituímos os valores encontrados no passo anterior para e :
Multiplicando tudo por , temos:
Aí, fazendo a distributiva do lado esquerdo:
Passando para o outro lado e colocando em evidência:
E isolando , encontramos que:
Por fim, substituindo:
- ;
- ;
- & ,
Encontramos que:
Resposta
Exercício Resolvido #3
Elaboração própria
Deseja-se construir uma peça a fim de que a peça passe por um vão, o problema é que para que essa peça ultrapasse o vão é necessário que a mesma sofra uma redução de seção como mostra a figura. Sabendo que essa peça somente será sujeita a esforços de flexão discorra sobre os principais problemas encontrados nessa redução de seção.
Passo 1
Aqui temos que lembrar dos conceitos de concentração de tensão em flexão. Sabemos que sempre que mudamos bruscamente as seções entre peças ocorre o que chamamos de concentração de tensão. Essa concentração de tensão é contabilizada no que chamamos de coeficiente de concentração de tensão, que é obtido graficamente pelo seguinte gráfico
O que percebemos é que o coeficiente de concentração de tensões aumenta o valor das tensões médias que ocorrem na mudança de seção. Isso é altamente perigoso, pois suponha que a peça trabalhe em estados próximos do rompimento, se colocarmos ainda um fator de concentração de tensão, podemos acabar aumentando as tensões médias ao ponto de ultrapassarem a tensão admissível do material, se isso ocorresse poderia causar acidentes catastróficos dependendo de onde a peça fosse usada.
É muito importante tomar cuidado com isso, pois somente deve ser usado variação de seção em casos que não seja possível manter a seção constante.
Caso seja necessário variar a seção, que seja da forma mais suave possível, para evitar altas concentrações de tensões e consequentemente riscos de rompimento da peça.
Vale lembrar que a tensão máxima em concentrações de tensões devido a ação da flexão é dada por
Como pelo gráfico vemos que o valor de K só pode ser maior que 1, significa que sempre haverá aumento das tensões médias, sempre podendo levar a peça ao risco de rompimento pela variação da seção.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração própria
Uma peça tinha seção constante. Mas na hora da construção do equipamento decidiu-se retirar um semicírculo na parte superior e inferior da peça, o semicírculo possui diâmetro pequeno e ambos estão na mesma seção, como mostra a figura abaixo.
Sabendo que a seção central representa uma seção crítica, explique através de conceitos e gráficos quais problemas esse novo formato trará a peça.
Passo 1
Temos que entender o seguinte, se a peça sofre uma redução de seção brusca, passamos a ter uma concentração de tensões. Essa concentração de tensões põe em risco a estruturas da peça, pelos seguintes motivos.
Primeiro temos que lembrar que a fórmula é dada por
E o K representa o coeficiente de concentração de tensões, que é calculado graficamente pelo gráfico dado abaixo
Percebemos que os valores de K começam diretamente de 1. Isso implica que a tensão cisalhante média será sempre aumentada, o cuidado que devemos tomar é que, algumas peças trabalham próximas do valor de rompimento, ou ainda, podem ser sujeitas a esforços não dimensionados. O problema é que a concentração de tensões aumenta o valor da tensão máxima. Isso é altamente perigoso, pois se a variação de seção for brusca o suficiente para produzir uma concentração de tensões tal que a tensão máxima ultrapasse a tensão admissível, teremos o rompimento da peça, o que pode ser catastrófico ou simplesmente uma perda gigantesca. Por isso é de suma importância analisar o quando a variação de seção contribui na concentração de tensões, e essa contribuição é contabilizada no que chamamos de coeficiente de concentração de tensão.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração própria
A tensão máxima medida na peça abaixo foi de 300Mpa. Sabendo que a seção maior tem dimensões (20x50) cm e a seção menor tem dimensões (20x30) cm sendo as seções representadas pela figura abaixo, determine qual o momento fletor atuante na nossa peça. O raio de adoçamento entre as seções é de 15cm.
Passo 1
Aqui nos temos que tomar o seguinte cuidado, vamos fazer o processo contrario do que estamos acostumados, primeiro vamos determinar os valores da nossa fórmula final e depois vamos abrindo cada parte da nossa fórmula.
A nossa fórmula final será a seguinte
Sabemos pelo enunciado que
Precisamos determinar o valor de K graficamente e só com isso já conseguimos determinar o valor de tensão média, então vamos lá.
Passo 2
Para determinar o valor do K precisamos seguir alguns planejamentos, primeiro vamos determinar a melhor curva pela relação
Em que cada letra está relacionada com a nossa peça pela imagem abaixo
Sabemos que pela nossa peça esses valores são
substituindo
Agora que já temos a melhor curva precisamos do valor horizontal, e para determinarmos esse valor usamos a relação
Já determinamos a melhor curva e o valor horizontal, agora só falta determinar o valor de K, que obtemos graficamente
Logo o valor de K será
Passo 3
Calculado esses dois valores vamos determinar a tensão média
Sabemos que a tensão média é calculada pela forma da flexão, então podemos escreve-la como
Substituindo na nossa equação os valores que já temos
Agora vem a grande pergunta, qual seção usar? a maior ou a menor?
Queremos maximizar a tensão, logo usamos a menor seção, pois quanto menor o momento de inercia, maior o valor da tensão, que é exatamente o que queremos. A menor seção é retangular com dimensões (20x30), logo a fórmula para fazer os cálculos são
Sabemos que as dimensões são
Em que Y é a metade da altura da menor seção
Substituindo os valores teremos que
Resposta
Exercício Resolvido #6
Elaboração própria
Determine a tensão Normal máxima na peça estrutural abaixo. A seção maior é dada por (45x90) mm e a seção menor é dada por (45x22,5) mm. Também sabe-se que o raio de adoçamento é de 6,75mm e o momento fletor atuante é de 500KN.m
Passo 1
Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será definir o valor da tensão média pela fórmula
Em que
Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.
A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.
- Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão
- Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação
Em que no nosso caso se trata da relação entre as alturas da nossa peça como mostra a figura
- E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação
Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula
Passo 2
Agora que já sabemos como calcular cada termo vamos a prática.
Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula
Em que sabemos que a menor seção é dada por
E para a tensão média temos que
Passo 3
Vamos agora determinar o coeficiente de concentração de tensão.
Sabemos que primeiro devemos usar um gráfico, que é esse aqui
Depois devemos determinar a melhor curva pela relação
Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula
Agora vamos determinar o valor do K
Passo 4
Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula
Resposta
Exercício Resolvido #7
Elaboração própria
Para a peça de madeira abaixo com seção retangular de espessura 7mm determine a maior tensão normal que ela será submetida caso seja sujeita a um momento fletor de .
Passo 1
Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será definir o valor da tensão média pela fórmula
Em que
Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.
A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.
- Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão
- Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação
Em que no nosso caso se trata da relação entre as alturas da nossa peça como mostra a figura
- E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação
Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula
Passo 2
Agora que já sabemos como calcular cada termo vamos a prática.
Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula
Em que sabemos que a menor seção é dada pela região central
E para a tensão média temos que
Passo 3
Vamos agora determinar o coeficiente de concentração de tensão.
Sabemos que primeiro devemos usar um gráfico, que é esse aqui
Depois devemos determinar a melhor curva pela relação
Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula
Agora vamos determinar o valor do K
Passo 4
Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula
Resposta
Exercício Resolvido #8
Elaboração própria
A barra de latão abaixo foi usada como suporte de uma estrutura. Sabendo que quando está com a seção continua a tensão admissível desse material é de , determine se essa mesma barra romperia com a ação de um momento fletor de na mesma, porém com seção variável.
Passo 1
Pra resolver esse exercício vamos dividir a solução em 3 partes. A primeira parte será definir o valor da tensão média pela fórmula
Em que
Aqui vale lembrar que usamos os valores da menor seção pois é nela que ocorrerá a maior tensão média, sempre lembre disso, usar os dados da menor seção, só usamos os valores da maior seção para definirmos o valor do coeficiente de concentração.
A segunda parte da nossa solução se trata de acharmos o coeficiente de concentração de tensão e para fazermos isso precisaremos de 3 coisas.
- Primeiro usar um gráfico para determinar o coeficiente de concentração de tensão
- Segundo devemos determinar qual a melhor curva do nosso gráfico para resolver o problema, e para isso usamos a relação
Em que no nosso caso se trata da relação entre as alturas da nossa peça como mostra a figura
- E por fim a terceira parte se trata de encontrarmos o valor no eixo horizontal do nosso gráfico, que encontraremos pela relação
Por fim a terceira parte da nossa solução será relacionar a tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula
Passo 2
Agora que já sabemos como calcular cada termo vamos a prática.
Como vimos a primeira parte da solução se trata de calcularmos a tensão cisalhante média pela fórmula
Em que sabemos que a menor seção é dada por
E para a tensão média temos que
Passo 3
Vamos agora determinar o coeficiente de concentração de tensão.
Sabemos que primeiro devemos usar um gráfico, que é esse aqui
Depois devemos determinar a melhor curva pela relação
Agora que já sabemos a melhor curva só falta determinar o valor horizontal, que determinamos pela fórmula
Agora vamos determinar o valor do K
Passo 4
Agora basta relacionarmos a nossa tensão cisalhante média com o coeficiente de concentração de tensão pela fórmula
Aqui vale ressaltar como podemos ter problemas com concentradores de tensão, pois se olharmos a nossa tensão média, vemos que ela é menor do que a nossa tensão admissível, ou seja,
Porém quando olhamos a nossa tensão máxima, com a contribuição do concentrador de tensões, temos que
Ou seja, a nossa peça sofre rompimento devido a concentração de tensões, por isso devemos tomar muito cuidado ao usarmos seções variáveis em algumas situações.
Resposta
A peça sofrerá um rompimento devido a variação de seção que causa uma concentração de tensão
Exercício Resolvido #9
Elaboração própria
A peça de aço mostrada pode suportar uma tensão de até . Sabendo que ocorre concentração de tensões devido a variação de seção, determine o máximo valor do momento fletor que podemos aplicar nessa peça sem que ela rompa.
Passo 1
Aqui nos temos que tomar o seguinte cuidado, vamos fazer o processo contrario do que estamos acostumados, primeiro vamos determinar os valores da nossa fórmula final e depois vamos abrindo cada parte da nossa fórmula.
A nossa fórmula final será a seguinte
Sabemos pelo enunciado que
Precisamos determinar o valor de K graficamente e só com isso já conseguimos determinar o valor de tensão média, então vamos lá.
Passo 2
Para determinar o valor do K precisamos seguir alguns planejamentos, primeiro vamos determinar a melhor curva pela relação
Em que cada letra está relacionada com a nossa peça pela imagem abaixo
Sabemos que pela nossa peça esses valores são
substituindo
Agora que já temos a melhor curva precisamos do valor horizontal, e para determinarmos esse valor usamos a relação
Já determinamos a melhor curva e o valor horizontal, agora só falta determinar o valor de K, que obtemos graficamente
Logo o valor de K será
Passo 3
Calculado esses dois valores vamos determinar a tensão média
Sabemos que a tensão média é calculada pela forma da flexão, então podemos escreve-la como
Substituindo na nossa equação os valores que já temos
Agora vem a grande pergunta, qual seção usar? a maior ou a menor?
Queremos maximizar a tensão, logo usamos a menor seção, pois quanto menor o momento de inercia, maior o valor da tensão, que é exatamente o que queremos. A menor seção é retangular com dimensões (13x36,24) mm, logo a fórmula para fazer os cálculos são
Sabemos que as dimensões são
Em que Y é a metade da altura da menor seção
Substituindo os valores teremos que
Resposta
Exercício Resolvido #10
Elaboração própria
A peça de seção variável abaixo sofre a ação de um esforço fletor. Sabendo que a mesma possui resistência máxima a ação do normal de , determine o máximo momento ao qual podemos submeter essa peça sem que ela rompa.
Passo 1
Aqui nos temos que tomar o seguinte cuidado, vamos fazer o processo contrario do que estamos acostumados, primeiro vamos determinar os valores da nossa fórmula final e depois vamos abrindo cada parte da nossa fórmula.
A nossa fórmula final será a seguinte
Sabemos pelo enunciado que
Precisamos determinar o valor de K graficamente e só com isso já conseguimos determinar o valor de tensão média, então vamos lá.
Passo 2
Para determinar o valor do K precisamos seguir alguns planejamentos, primeiro vamos determinar a melhor curva pela relação
Em que cada letra está relacionada com a nossa peça pela imagem abaixo
Sabemos que pela nossa peça esses valores são
substituindo
Agora que já temos a melhor curva precisamos do valor horizontal, e para determinarmos esse valor usamos a relação
Em que
Já determinamos a melhor curva e o valor horizontal, agora só falta determinar o valor de K, que obtemos graficamente
Logo o valor de K será
Passo 3
Calculado esses dois valores vamos determinar a tensão média
Sabemos que a tensão média é calculada pela forma da flexão, então podemos escreve-la como
Substituindo na nossa equação os valores que já temos
Agora vem a grande pergunta, qual seção usar? a maior ou a menor?
Queremos maximizar a tensão, logo usamos a menor seção, pois quanto menor o momento de inercia, maior o valor da tensão, que é exatamente o que queremos. A menor seção é retangular com dimensões (3x27) mm, logo a fórmula para fazer os cálculos são
Sabemos que as dimensões são
Em que Y é a metade da altura da menor seção
Substituindo os valores teremos que