Fórmula do Cisalhamento
Produzido por Pablo RicardoTeoria
Introdução
Nos assuntos anteriores, nós vimos:
Como cargas axiais em uma peça geram nela forças internas normais e tensões normais :
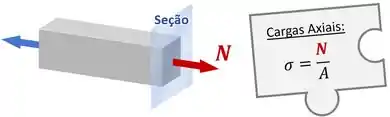
E como torques em uma peça geram nela torques internos (ou momentos torsores ), que geram na peça tensões cisalhantes de acordo com a fórmula da torção:
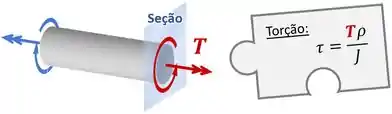
Além disso, também vimos:
Como as cargas transversais em uma viga geram nela forças cortantes/cisalhantes e momentos fletores :
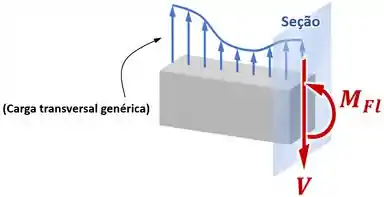
Sendo que quanto a esse momento fletor , vimos que ele gera tensões normais de acordo com a fórmula da flexão:
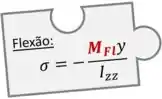
Então agora, só tá faltando para a gente a última peça do “quebra-cabeça” de resistência dos materiais:
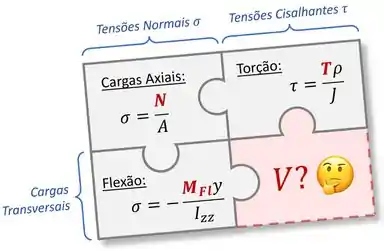
Que é: como são as tensões causadas pela força cortante em uma peça?
De cara, como a própria força cortante é chamada também de força de cisalhamento, dá para concluir que essas tensões vão ser tensões cisalhantes (“tau”).
Mas como podemos descrever essas tensões ?
Exemplo
Para ilustrar essa pergunta, vamos usar um exemplo:
Vamos dizer que, em uma questão da sua prova, você precisa determinar a tensão máxima causada pela força cortante na viga em “” abaixo:
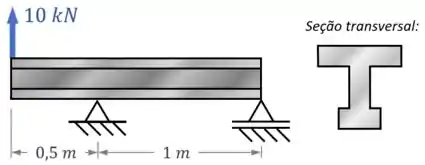
Avaliando os esforços internos nessa viga, você descobre que a força cortante máxima nela ocorre no trecho inicial, onde :
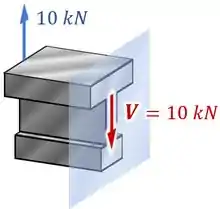
Mas e agora? 🤔
Como podemos descrever as tensões causadas por essa força cisalhante ?
Fórmula do Cisalhamento
A solução está em usar a fórmula do cisalhamento:
Essa fórmula fornece a tensão de cisalhamento causada pela força cortante em uma dada fibra de uma seção transversal:
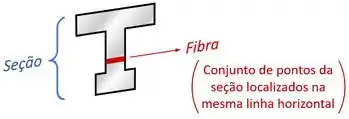
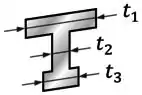
Sendo que nessa fórmula:
- ou é o momento estático (que vamos aprender a calcular em breve!), calculado para uma certa fibra da seção;
- ou é o momento de inércia da área da seção; (Igual ao que era utilizado lá na fórmula da flexão!)
- & ou é a largura da fibra em que se quer calcular a tensão :
Beleza...
Mas como a gente aplica essa fórmula na prática?
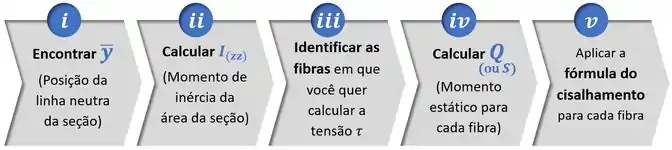
Seguindo a sequência de passos abaixo!

Entre esses passos, os dois primeiros nós já vimos lá quando estudamos a fórmula da flexão e estão resumidos no quadro abaixo:
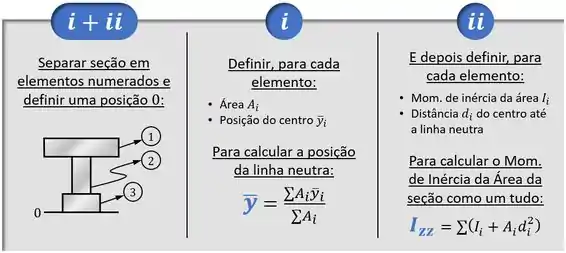
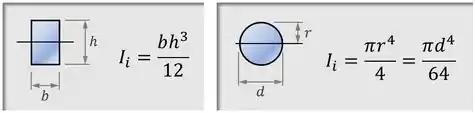
Sendo que o momento de inércia da área de cada elemento retangular ou circular é dado pelas fórmulas:
Já os outros 3 passos são passos novos: nunca vimos eles antes.
Então vamos ver como fazê-los um a um!
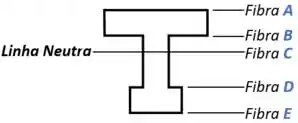
Identificação das Fibras
Após determinarmos a posição da linha neutra e o momento de inércia da área para a nossa seção, o próximo passo é identificar as fibras da seção nas quais queremos calcular a tensão .
Nesse passo, as fibras importantes de serem identificadas são:
- As fibras no topo e na base da seção;
- As fibras nas regiões em que há uma mudança na geometria da seção;
- & a fibra na linha neutra da seção.
Por exemplo, para a nossa viga em , essa identificação pode ficar assim:
Momentos Estáticos
Em seguida, calculamos os momentos estáticos ou para cada fibra identificada no passo anterior.
Para tanto, devemos fazer o seguinte:
- Observar somente a região acima OU abaixo da fibra:
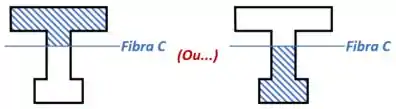
- Separar a região escolhida em elementos individuais:

- Identificar, para cada um desses elementos, a área e a posição do seu centro em relação à linha neutra da seção:
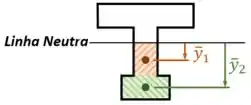
- E finalmente, aplicar a fórmula (ou ) para a fibra em questão:
- A distribuição de tensões devido à força cortante é parabólica;
- E de que o ponto máximo dessas parábolas ocorre sempre na linha neutra da seção.
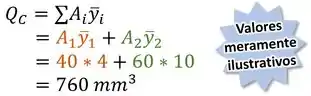
Sendo que durante a resolução de um exercício, não é preciso fazer esse passo tão detalhado como nas imagens acima!
Simplesmente identificar as fibras e calcular os valores numéricos de ou para cada fibra é o suficiente, como na imagem abaixo:

Por fim, ainda existem algumas dicas sobre o momento estático ou que foram utilizadas na imagem acima e que você pode usar a vontade para facilitar a sua vida:

Aplicação da Fórmula do Cisalhamento
Finalmente, após termos calculado os momentos estáticos no passo anterior, podemos calcular as tensões nas nossas fibras.
Aqui, devemos aplicar a fórmula do cisalhamento para cada fibra, tomando o cuidado de usar o momento estático ou correto e a largura da fibra ou correta.
Além disso, para as fibras onde há uma mudança de largura, devemos aplicar a fórmula do cisalhamento duas vezes: uma para cada largura.
Fazendo tudo isso para o nosso exemplo da viga em e marcando esses pontos em um gráfico, teríamos algo assim:
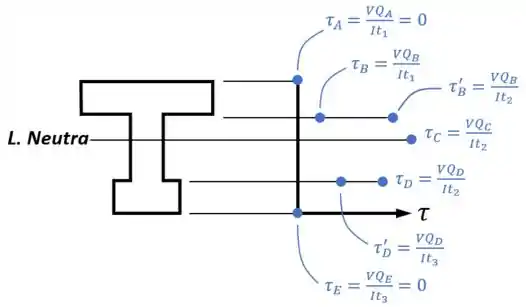
E as tensões nos demais pontos?
Você pode indicar elas conectando os pontos do gráfico acima, tendo em mãos o conhecimento de que:
E pronto!
Conectando os pontos dessa forma, encontramos que as tensões na nossa seção ficam assim:
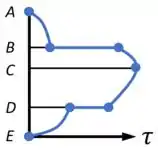
Aí a partir desse gráfico, você consegue reconhecer a tensão cisalhante máxima devido à força cortante na viga.
Nesse caso, vemos que a tensão máxima acontece na fibra .
Resumão
Agora você está preparado para fazer os exercícios resolvidos a seguir e mandar bem na prova!
Para te ajudar, segue um resumão dos passos para resolver esses exercícios:
Exemplo
Fórmula do Cisalhamento
Identificação das Fibras
Momentos Estáticos
Aplicação da Fórmula do Cisalhamento
Resumão
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 272&273-7.6.
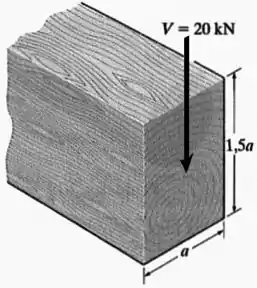
A viga tem seção transversal retangular e é feita de madeira com tensão de cisalhamento admissível . Se for submetida a um cisalhamento , determine a menor dimensão de sua parte inferior e de seus lados.
Passo 1
O que está acontecendo?
A seção transversal dessa viga é retangular, com uma base e uma altura .
Por causa da força cortante , vão surgir nessa seção tensões de cisalhamento de acordo com a fórmula do cisalhamento:
Onde:
- (também conhecido como “”) é o momento estático, calculado para uma fibra da seção;
- (também conhecido como ) é o momento de inércia da área da seção;
- & (também conhecido como ) é a largura da fibra em que se quer calcular a tensão .
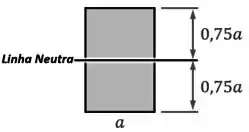
Aí, como a seção dessa viga é só um retângulo, já sabemos que a sua linha neutra/centroide fica bem no meio da seção:
Além disso:
- O momento de inércia da área é sempre uma constante;
- E essa seção tem uma largura constante.
Então o que vai determinar aonde vai ocorrer a tensão máxima nessa seção é o momento estático .
E nós vimos na nossa teoria que o momento estático é sempre máximo na linha neutra:

Assim, concluímos que a tensão máxima nesse seção vai ocorre na sua linha neutra.
E o que é que o exercício quer?
Ele quer saber qual é o menor valor de necessário para que a tensão de cisalhamento máxima nessa viga não ultrapasse o seu valor admissível .
Ou seja, ele quer saber qual é o menor valor de que satisfaz a condição:
Então, para resolver esse exercício...
Devemos determinar o valor de para essa seção e depois determinar o valor do momento estático para a fibra na linha neutra.
Assim, vamos poder descrever a tensão nessa seção em função da dimensão .
Substituindo isso na condição acima, vamos poder isolar e encontrar seu valor mínimo necessário.
Passo 2
Então vamos começar pelo cálculo do momento de inércia da área para essa seção retangular.
Lembra aí!
O momento de inércia da área de um elemento retangular é dado pela fórmula:
Daí que, substituindo os valores:
- ;
- & ,
Encontramos que:
O que dá:
Beleza!
Passo 3
Em seguida, vamos determinar o valor do momento estático para a linha neutra, que é sempre o momento estático máximo em uma seção:
Agora lembra aí!
Para determinar o valor do momento estático, devemos:
- Observar somente a região acima OU abaixo da fibra;
- Separar a região escolhida em elementos individuais;
- Identificar, para cada elemento, a área e a posição do seu centro em relação à linha neutra da seção;
- E finalmente, aplicar a fórmula para a fibra em questão.
Fazendo isso para a fibra na linha neutra, e escolhendo observar a região acima dela, vamos ter um único elemento retangular, com a área e posição indicadas na imagem abaixo:
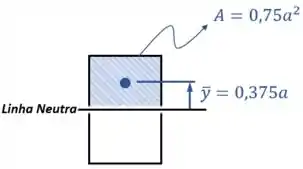
Dessa forma, vamos ter que:
O que significa que:
E pronto!
Passo 4
Agora, podemos pegar a nossa condição de projeto:
E aplicar a fórmula do cisalhamento com o objetivo de descrever a tensão máxima nessa seção.
Fazendo isso, a nossa condição fica assim:
Substituindo , e , vamos ter que:
Simplificando isso, temos:
Isolando :
Espelhando essa expressão e fazendo a raíz quadrada dos dois lados:
E substituindo:
- ;
- & ,
Encontramos que:
O que significa que o valor mínimo necessário para a dimensão é:
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 273-7.10.
Faça um gráfico da intensidade da tensão de cisalhamento distribuída na seção transversal da escora se ela for submetida a uma força de cisalhamento .
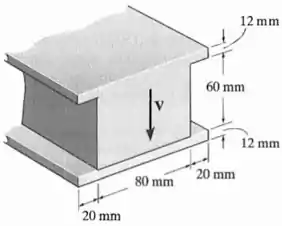
Passo 1
O que está acontecendo?
Por causa da força cortante , vão surgir nessa seção tensões de cisalhamento de acordo com a fórmula do cisalhamento:
Onde:
- (também conhecido como “”) é o momento estático, calculado para uma fibra da seção;
- (também conhecido como ) é o momento de inércia da área da seção;
- & (também conhecido como ) é a largura da fibra em que se quer calcular a tensão .
Além disso, como essa seção é simétrica em relação à horizontal, já sabemos que a sua linha neutra/centroide fica bem no seu meio:
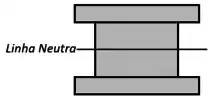
E o que é que o exercício quer?
Ele quer que a gente esboce um gráfico da intensidade da tensão de cisalhamento distribuída nessa seção.
Para fazer isso, devemos seguir os passos abaixo:
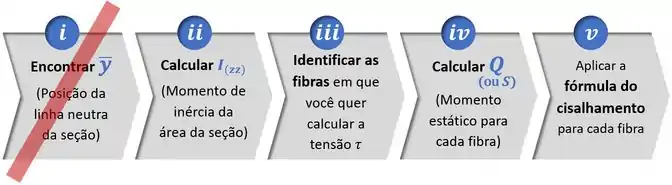
Sendo que no nosso caso, já conhecemos a posição da linha neutra, então podemos pular esse passo.
Aí, depois de aplicarmos a fórmula do cisalhamento para cada fibra, vamos poder colocar os resultados para a tensão em um gráfico e conectar esses pontos, completando o gráfico pedido pelo exercício!
Passo 2
Então vamos lá!
Primeiro, precisamos fazer o cálculo do momento de inércia da área para essa seção.
Para tanto, começamos separando a seção em elementos numerados:
Feito isso, calculamos:
- o momento de inércia da área ;
- a área ;
- e a distância de seu centro até a linha neutra,
...para cada um desses elementos.
Todos os elementos são retangulares, então eles vão ter áreas e momentos dados pela fórmula:
Observando as dimensões fornecidas pelo exercício, vemos que para os elementos e , temos uma base e uma altura , de tal forma que:
Já para o elemento , temos uma base e uma altura , de tal forma que:
Por fim, observando mais uma vez as dimensões fornecidas pelo exercício, encontramos as distâncias e dos centros dos elementos e à linha neutra:
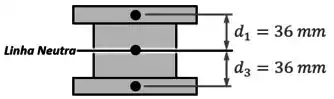
E como o centro do elemento já está na própria linha neutra, vamos ter que:
Feito tudo isso, podemos finalmente aplicar a fórmula:
...para determinar o momento de inércia da área da nossa seção como um todo:
Como , e , podemos re-escrever essa fórmula assim:
Finalmente, substituindo todos os valores disponíveis acima, encontramos que:
Ou então:
Passo 3
Agora, vamos identificar as fibras que nos interessam nessa viga, que são:
- As fibras no topo e na base da seção;
- As fibras nas regiões em que há uma mudança na geometria da seção;
- & a fibra na linha neutra da seção.
Fazendo isso, devemos ter um desenho assim:
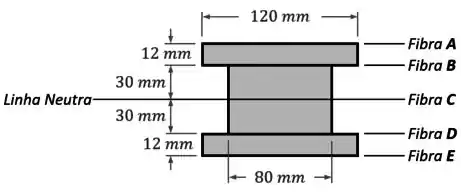
Sendo que nesse desenho, as dimensões foram adicionadas para facilitar já os nossos cálculos no próximo passo.
Passo 4
Identificadas as fibras, podemos calcular os momentos estáticos delas.
Nesse momento, vão nos ajudar as dicas que vimos na teoria:

Assim, para as fibras e , no topo e na base da seção, já sabemos que elas vão ser iguais à :
Em seguida, por simetria, podemos dizer que os momentos estáticos para as fibras e vão ser iguais:
Para calcular esses momentos estáticos, podemos escolher observar a região acima da fibra .
Nessa região, vamos ter um único elemento retangular, de área e com uma posição do centro em relação à linha neutra , de tal forma que:
Por fim, para calcular o momento estático , podemos observar a região acima da fibra .
Nessa região, vamos ter:
- O mesmo elemento retangular que havia na região acima da fibra , para o qual e ;
- E um elemento retangular encostando na linha neutra, de base e altura , tendo assim uma área e uma posição .
Dessa forma, temos que:
Passo 5
Por fim, podemos aplicar a fórmula do cisalhamento:
...para cada fibra, tomando o cuidado de aplicar essa fórmula duas vezes para as fibras em que existem dois valores da largura .
(Nesse caso, temos que tomar esse cuidado para as fibras e , onde há uma mudança na largura da seção.)
Começando pelas fibras e :
Como o momento estático para essas fibras é igual à , vamos ter que:
Já para as fibras e , temos:
Substituindo os valores:
- ;
- ;
- ,
E utilizando o valor maior da largura para essas fibras, , encontramos que:
Calculando tudo isso, vamos ter um resultado final em ou :
Em seguida, utilizando o valor menor da largura para essas fibras, , encontramos que:
O que dá:
Por fim, para a fibra , temos:
E substituindo:
- ;
- ;
- ,
E a largura da seção na região da fibra , , encontramos que:
Passo 6
Finalmente, inserindo os valores de tensão encontrados no passo anterior em um gráfico, e conectando esses pontos sabendo que:
- A distribuição de tensões devido à força cortante é parabólica;
- E de que o ponto máximo dessas parábolas ocorre sempre na linha neutra da seção.
Ficamos com o gráfico abaixo, que é a nossa resposta para o exercício:
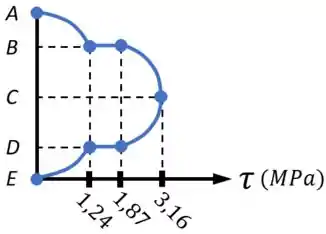
Resposta
Exercício Resolvido #3
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 273-7.14.
Se a viga for submetida a um cisalhamento vertical , determine a tensão de cisalhamento máxima na viga. Calcule também o salto da tensão de cisalhamento na junção aba-alma . Trace um rascunho da variação da intensidade da tensão de cisalhamento em toda a seção transversal.
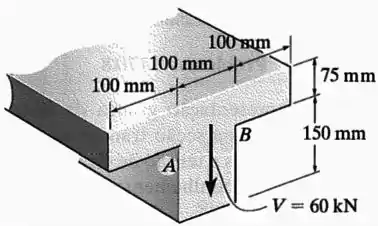
Passo 1
O que está acontecendo?
Por causa da força cortante , vão surgir nessa seção tensões de cisalhamento de acordo com a fórmula do cisalhamento:
Onde:
- (também conhecido como “”) é o momento estático, calculado para uma fibra da seção;
- (também conhecido como ) é o momento de inércia da área da seção;
- & (também conhecido como ) é a largura da fibra em que se quer calcular a tensão .
E o que é que o exercício quer?
Ele quer saber:
- A tensão de cisalhamento máxima nessa seção;
- E o salto de tensão na junção aba-alma , que é a diferença entre a tensão nessa região para a aba de largura e a tensão nessa região para a alma de largura .
Para encontrar essas duas coisas, vamos ter que esboçar um gráfico para a distribuição da tensão nessa seção, que é a terceira coisa que o exercício pede.
Aí, para fazer isso, é só seguirmos os passos abaixo:
Então vamos lá!
Passo 2
Primeiro, precisamos determinar a posição da linha neutra dessa seção.
Para tanto, começamos separando a seção em elementos numerados e definindo uma posição na base da seção:
Em seguida, preenchemos em uma tabela os valores da área e da posição do centro de cada elemento:
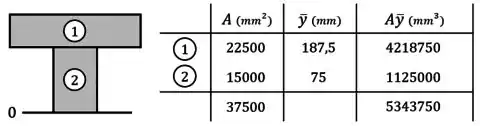
Ainda nessa tabela, também preenchemos na última coluna o produto desses valores para cada elemento e na última linha os somatórios e .
Com isso, podemos aplicar a fórmula:
E substituir os valores desses somatórios para encontrarmos a posição da nossa linha neutra:
Passo 3
Agora, já podemos calcular o momento de inércia da área da nossa seção como um todo.
Para tanto, devemos calcular, para cada elemento numerado:
- O momento de inércia da área ;
- E a distância do centro do elemento até a linha neutra.
(Não precisamos calcular as áreas pois já calculamos elas no passo anterior.)
Como os nossos dois elementos são retangulares, eles vão momentos de inércia da área .
Para o elemento , temos uma base e uma altura , então:
Já para o elemento , e , então:
Em seguida, como o elemento tem um centro a uma altura de e como a linha neutra está a uma altura de , a distância para o elemento vai ser:
Já o elemento tem um centro a uma altura de , de tal forma que:
Finalmente, podemos aplicar a fórmula:
Que fica assim para o nosso caso com dois elementos:
E substituir nessa fórmula:
- e ;
- e ; (Valores retirados da tabela do passo anterior)
- & e ,
Para encontrarmos que o momento de inércia da área da nossa seção como um todo é:
Passo 4
Próximo passo, identificar as fibras de interesse:
- As fibras no topo e na base da seção;
- As fibras onde ocorre uma mudança na largura da seção;
- E a fibra na linha neutra.
Fazendo isso, ficamos com o desenho abaixo:
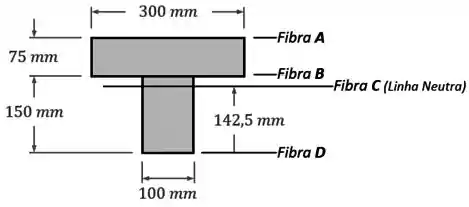
Sendo que nesse desenho, as dimensões foram adicionadas para já facilitar os cálculos do próximo passo.
Passo 5
Agora, devemos calcular os momentos estáticos .
Para as fibras e , podemos nos lembrar que os momentos estáticos das fibras no topo e na base de uma seção são iguais a zero, então:
Para a fibra , podemos escolher por observar a região acima dessa fibra.
Fazendo isso, vamos ter nessa região um único elemento retangular: o elemento que definimos anteriormente.
Esse elemento tem uma área e um centro com uma posição relativa à linha neutra .
Dessa forma, temos que:
Já para a fibra , é mais fácil escolher por observar a região abaixo desse fibra.
Nessa região, vamos ter um único elemento retangular encostado na linha neutra com uma altura de e uma largura de .
Dessa forma, esse elemento vai ter uma área e um centro com uma posição relativa à linha neutra .
Sendo assim, temos:
Passo 6
Finalmente, já temos tudo que precisamos para aplicar a fórmula do cisalhamento:
...para cada fibra.
Para as fibras e , como , vamos ter que:
Já para a fibra , temos:
Aí, como temos duas larguras na região da fibra ( e ), devemos aplicar essa fórmula duas vezes.
Primeiro, substituímos:
- ;
- ;
- ,
E a largura da aba, :
Calculando tudo, vamos ter um resultado final em , que é o mesmo que :
Em seguida, substituímos os mesmos valores, mas dessa vez utilizamos a largura da alma, :
Calculando tudo isso, encontramos que:
Por fim, para a fibra , temos:
Aí, substituindo:
- ;
- ;
- ;
- E a largura da seção na região da fibra , ,
Encontramos que:
Passo 7
Por fim, inserindo os valores de tensão encontrados no passo anterior em um gráfico, e conectando esses pontos sabendo que:
- A distribuição de tensões devido à força cortante é parabólica;
- E de que o ponto máximo dessas parábolas ocorre sempre na linha neutra da seção.
Ficamos com o gráfico abaixo, que faz parte da nossa resposta para o exercício:
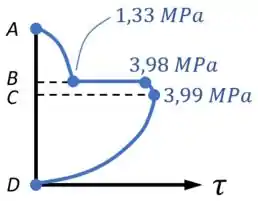
Além disso, desse gráfico...
Conseguimos identificar a tensão de cisalhamento máxima nessa seção e o valor do salto de tensão na junção aba-alma na fibra , que completam a nossa resposta para o exercício:
Resposta
Exercício Resolvido #4
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 273-7.11.
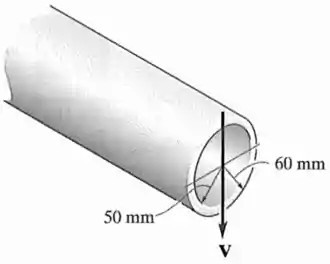
Se o tubo estiver sujeito a um cisalhamento , determine a tensão de cisalhamento máxima nele.
Dicas do Expert: Existem alguns conhecimentos adicionais importantes para resolver exercícios com uma seção circular como este.
São eles:
1. A tensão de cisalhamento máxima em seções transversais circulares (vazadas ou não) ocorre na linha neutra da seção;
2. Para o cálculo da posição da linha neutra, do momento de inércia da área e do momento estático, você pode considerar furos como elementos de área negativa e momento de inércia da área negativo;
& 3. A centroide de um semicírculo de raio fica a uma distância da base do semicírculo.
Passo 1
O que está acontecendo?
A seção transversal dessa viga tem a forma de um anel, com raio externo e raio interno .
Por causa da força cortante , vão surgir nessa seção tensões de cisalhamento de acordo com a fórmula do cisalhamento:
Onde:
- (também conhecido como “”) é o momento estático, calculado para uma fibra da seção;
- (também conhecido como ) é o momento de inércia da área da seção;
- & (também conhecido como ) é a largura da fibra em que se quer calcular a tensão .
Além disso, como essa seção é simétrica em relação à horizontal, já podemos afirmar que a sua linha neutra fica bem no seu meio:
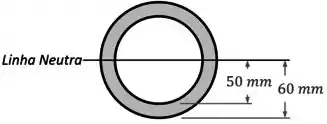
E o que é que o exercício quer?
Ele quer saber a tensão de cisalhamento máxima nessa seção, que vai ocorrer na sua linha neutra.
Então, devemos encontrar:
- O momento de inércia da área dessa seção;
- E o momento estático para a fibra na linha neutra.
Feito isso, vamos poder aplicar a fórmula do cisalhamento para a fibra na linha neutra “”, que vai ficar assim:
Sendo que a largura da seção nessa fibra vai ser igual ao diâmetro externo de menos o diâmetro interno de .
Ou seja, .
Passo 2
Então vamos começar calculando o momento de inércia da área para essa seção.
Para tanto, devemos separar ela em elementos individuais.
Nesse caso, podemos considerar o círculo maior como um elemento e o círculo menor, que é um furo, como um elemento de área negativa e momento negativo:
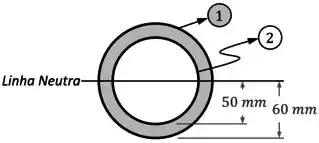
Como ambos os elementos são circulares, os seus momentos de inércia da área individuais vão ser dados pela fórmula:
Assim, para o elemento , de raio , vamos ter que:
Enquanto que para o elemento , de área/momento negativo e de raio , temos:
Aí, como os dois elementos já estão centrados na linha neutra, não é necessário utilizar o teorema dos eixos paralelos .
Ao invés disso, podemos simplesmente somar os momentos de cada elemento para encontrarmos o valor do momento de inércia da área da seção como um todo:
Passo 3
Em seguida, calculamos o momento estático para a fibra na linha neutra.
Para tanto, podemos escolher observar a região acima dessa fibra.
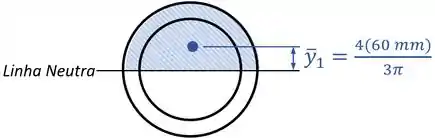
Fazendo isso, vamos ter dois elementos na forma de semicírculos.
O primeiro elemento, de raio , vai ter uma área positiva igual à metade da área de um círculo com esse raio:
E um centro com uma posição :
Já o segundo elemento, de raio , vai ter uma área negativa igual à metade da área de um círculo come esse raio:
E um centro com uma posição :
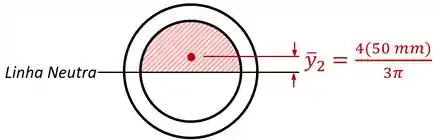
Dessa forma, o momento estático para a fibra na linha neutra vai ser:
O que dá:
Passo 4
Agora, só falta aplicar a fórmula do cisalhamento para o cálculo da tensão de cisalhamento máxima nessa seção, que ocorre na sua linha neutra.
Fazendo isso, temos:
Aí, substituindo:
- ;
- ;
- ;
- & ,
Vamos ter:
Calculando tudo e percebendo que o resultado final vai sair em , que é o mesmo que , encontramos que:
Resposta
Exercício Resolvido #5
Elaboração própria
Abaixo é dada uma seção retangular de altura 40cm e base 20 cm. Sabendo que a seção somente suporta uma tensão cisalhante de no máximo 500Kpa, determine a que altura ocorreria a tensão cisalhante imediatamente anterior ao rompimento da mesma. Vale ressaltar que a peça está sofrendo a ação de um cortante de 200KN na direção mostrada.
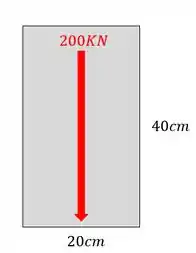
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata da altura em que alcançamos o cisalhante admissível da nossa peça, que também já sabemos ser 80Mpa).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
Passo 2
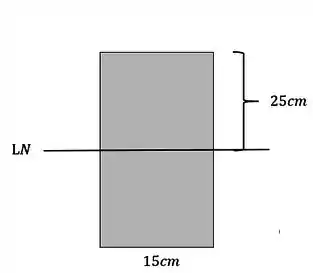
O primeiro passo é determinar a posição da linha Neutra. Como se trata de uma seção retangular, sabemos que a linha neutra passa no centro da nossa seção, como mostra a figura
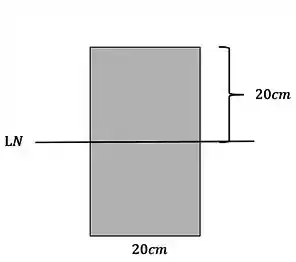
Também temos pelo enunciado dois valores
Um valor é o cortante
O outro valor é o próprio cisalhante
Passo 3
Também sabemos que devemos garantir o valor do momento de inércia, pois esse se trata diretamente do valor referente a seção, ou seja, independente do ponto em que calculamos o cisalhante.
Como se trata de uma seção retangular, sabemos que o momento de inercia será dado por
Como já vimos sabemos que
Substituindo teremos que
Também sabemos que a seção que iremos calcular tem espessura constante, que é o próprio valor de B, logo teremos que
Até aqui tudo bem, agora precisamos determinar o nosso momento estático.
Passo 4
Sabemos que a fórmula do momento estático é dada por
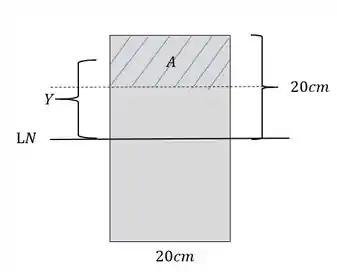
Em que é a área da seção acima do ponto em que estamos calculando o cisalhante e é o centroide que calculamos para essa área, porém em que ponto estamos calculando o cisalhante? Vamos ver a imagem abaixo para facilitar o entendimento.
como não sabemos a altura em que o cisalhante ocorre, vamos supor que esse valor seja o nosso X, dessa forma nossa figura ficará
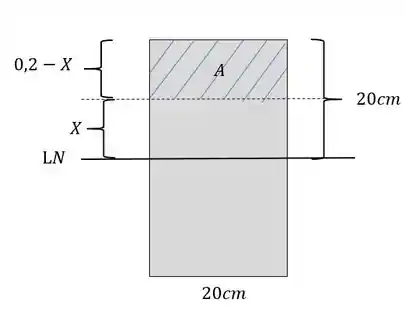
Então teremos que
Logo nosso momento estático será dado por
Passo 5
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que
Ou seja, a nossa peça sofreria rompimento no trecho distante 18,6 cm da linha neutra, ou seja, antes mesmo do cisalhante máximo que ocorreria na Linha Neutra.
Resposta
Nossa peça sofre rompimento a altura de 18,6 cm com relação a Linha Neutra
Exercício Resolvido #6
Elaboração própria
Abaixo é dado uma viga sujeita as cargas mostradas. Com base nos seus conhecimentos, determine a tensão cisalhante máxima que afeta a viga mostrada abaixo.
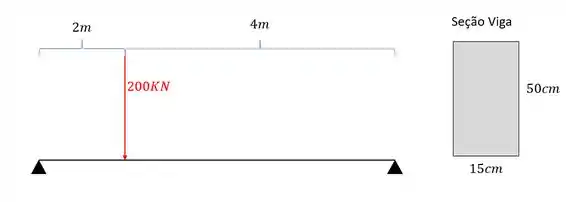
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata da altura em que alcançamos o cisalhante admissível da nossa peça, que também já sabemos ser 80Mpa).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
Passo 2
O primeiro passo é determinar a posição da linha Neutra. Como se trata de uma seção retangular, sabemos que a linha neutra passa no centro da nossa seção, como mostra a figura
Também precisamos saber qual o cortante está agindo na nossa peça, e para fazermos isso precisamos determinar o diagrama de esforços cortantes na nossa estrutura, para isso faremos primeiro a determinação das reações de apoio.
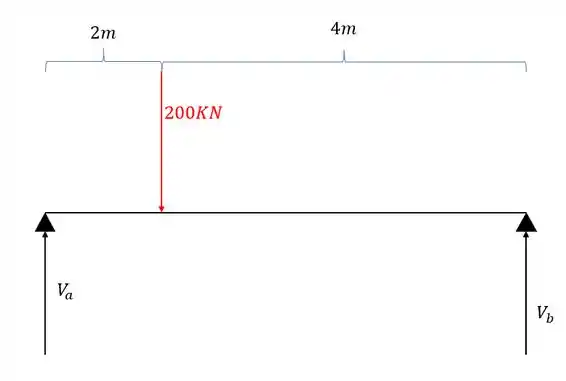
Sabemos que precisamos determinar o equilíbrio de forças. Para isso farei o somatório de momentos em A, assim teremos que
Como queremos que o somatório das reações também anule a carga teremos que
Passo 3
Como é pedido o cisalhante máximo, precisamos saber qual o maior cortante agindo na viga, vamos analisar então o diagrama de cortante.
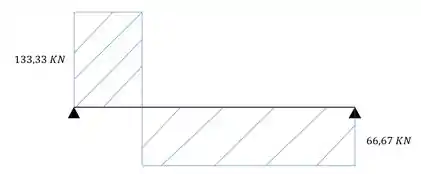
Por esse diagrama de cortantes teremos que o maior cortante agindo na nossa peça é
Passo 4
Também sabemos que devemos garantir o valor do momento de inércia, pois esse se trata diretamente do valor referente a seção, ou seja, independente do ponto em que calculamos o cisalhante.
Como se trata de uma seção retangular, sabemos que o momento de inercia será dado por
Como já vimos sabemos que
Substituindo teremos que
Também sabemos que a seção que iremos calcular tem espessura constante, que é o próprio valor de B, logo teremos que
Até aqui tudo bem, agora precisamos determinar o nosso momento estático.
Passo 5
Sabemos que a fórmula do momento estático é dada por
Em que é a área da seção acima do ponto em que estamos calculando o cisalhante e é o centroide que calculamos para essa área, porém em que ponto estamos calculando o cisalhante? Vamos ver a imagem abaixo para facilitar o entendimento.

Como querermos determinar o cisalhante máximo, devemos calcular o valor do momento estático que age na linha neutra da nossa seção.
Pelo nosso esquema teremos que
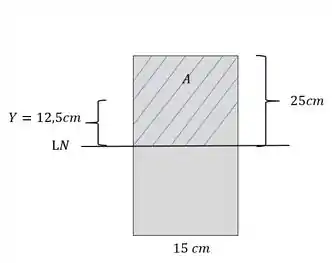
Com isso sabemos que a nossa área é dada por
E que
Logo nosso momento estático será
Passo 6
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que
Resposta
Exercício Resolvido #7
Elaboração própria
Calcule o valor do cisalhante máximo que ocorre na seção dada abaixo.
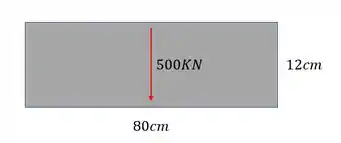
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata da altura em que alcançamos o cisalhante admissível da nossa peça, que também já sabemos ser 80Mpa).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
Passo 2
O primeiro passo é determinar a posição da linha Neutra. Como se trata de uma seção retangular, sabemos que a linha neutra passa no centro da nossa seção, como mostra a figura
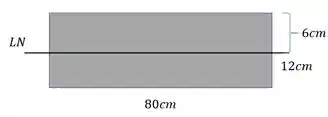
Também precisamos saber qual o cortante está agindo na nossa peça, e já sabemos seu módulo pelo enunciado.
Passo 3
Também sabemos que devemos garantir o valor do momento de inércia, pois esse se trata diretamente do valor referente a seção, ou seja, independente do ponto em que calculamos o cisalhante.
Como se trata de uma seção retangular, sabemos que o momento de inercia será dado por
Como já vimos sabemos que
Substituindo teremos que
Também sabemos que a seção que iremos calcular tem espessura constante, que é o próprio valor de B, logo teremos que
Até aqui tudo bem, agora precisamos determinar o nosso momento estático.
Passo 4
Sabemos que a fórmula do momento estático é dada por
Em que é a área da seção acima do ponto em que estamos calculando o cisalhante e é o centroide que calculamos para essa área, porém em que ponto estamos calculando o cisalhante? Vamos ver a imagem abaixo para facilitar o entendimento.
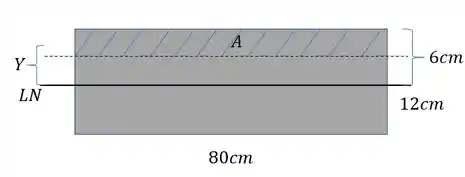
Como querermos determinar o cisalhante máximo, devemos calcular o valor do momento estático que age na linha neutra da nossa seção.
Pelo nosso esquema teremos que
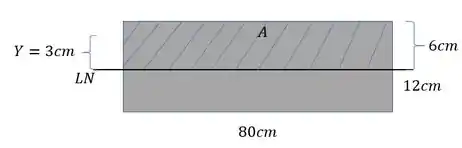
Com isso sabemos que a nossa área é dada por
E que
Logo nosso momento estático será
Passo 5
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que
Resposta
Exercício Resolvido #8
Elaboração própria
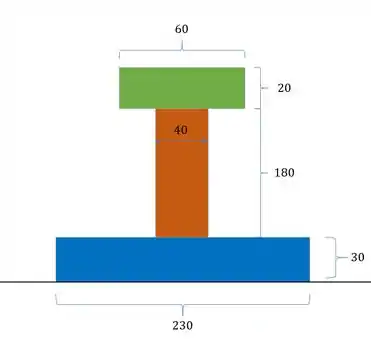
Determine a tensão cisalhante máxima na seção sujeita ao esforço cortante mostrado abaixo. Todas as medidas estão em cm.
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata da altura em que alcançamos o cisalhante admissível da nossa peça, que também já sabemos ser 80Mpa).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
Passo 2
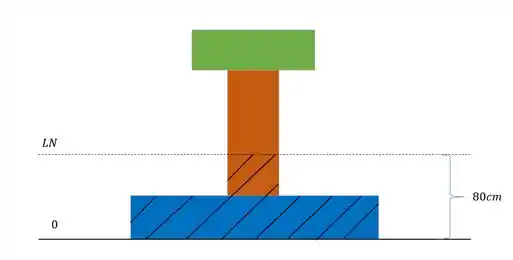
Precisamos determinar primeiramente a linha neutra na nossa seção. Sabemos que para determinarmos a linha neutra precisamos primeiro definir uma linha de origem, que geralmente passamos pela base da nossa seção.

Em seguida dividimos a nossa seção em figuras mais simples

Agora vem a parte legal, para cada uma dessas seções mais simples calculamos o valor da área e a distancia do centroide de cada uma delas até a nossa linha de origem.
Agora para determinar a linha neutra basta usar a fórmula
Teremos que a linha neutra será marcada com relação a nossa origem
Sabemos também que o nosso cortante é dado no enunciado e sabemos que vale
Passo 3
Precisamos definir agora o valor do nosso momento de inércia. Aqui devemos seguir um passo a passo como seguimos para determinação da linha neutra.
Vamos utilizar a mesma separação de figuras mais simples que usamos para determinação da linha neutra

Já sabemos quanto valem as áreas de cada seção, mas agora devemos calcular dois valores importantes. Primeiro o momento de inercia de cada uma das peças mais simples. Depois a distancia do centroide de cada peça até a linha neutra. Na figura abaixo já verificamos tanto as áreas quando as distâncias dos centroides até a linha neutra.
Vamos agora determinar o valor do momento de inercia para cada uma das peças. Sabemos que como todas são retângulos, a fórmula será
Olhando novamente as medidas teremos que
Logo
Com todos esses valores devemos usar a seguinte fórmula para determinarmos o momento de inercia da nossa seção
Substituindo nossos valores teremos que
Passo 4
Agora vamos determinar o momento estático da nossa seção. Como no enunciado foi pedido o valor do cisalhante máximo, devemos fazer o calculo levando em consideração as fibras da seção que contem a linha neutra, nesse caso a seção que usamos a cor laranja, dessa forma também descobrimos que o valor da espessura de fibras usada no nosso cálculo será
Mas também queremos determinar o momento estático, nesse caso devemos escolher a seção acima da linha neutra ou abaixo da linha neutra. Analisando a nossa seção, me parece mais simples fazer a conta analisando a parte de baixo da nossa seção, nesse caso pela nossa figura a nossa seção analisada será
Podemos ver que essa região marcada em baixo possui duas seções diferentes, uma azul e uma laranja, dessa forma, para calcularmos o momento estático total precisaremos determinar o momento estático de cada um desses trechos e soma-los. Mas como calculamos o momento estático?
A fórmula é dada por
Em que é a área de cada seção abaixo da linha neutra e a distancia do centroide de cada seção abaixo da linha neutra até a própria linha neutra. No esquema abaixo descobrimos que esses valores são os da figura
Agora basta substituir na fórmula os valores encontrados
Passo 5
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que
Resposta
Exercício Resolvido #9
Elaboração própria
Uma viga de seção retangular com as dimensões mostradas na figura, foi submetida a um carregamento cortante de intensidade . Sabendo que a tensão cisalhante admissível máxima suportada por essa viga é , determine o valor do cortante máximo que podemos aplicar sem que haja rompimento da peça.
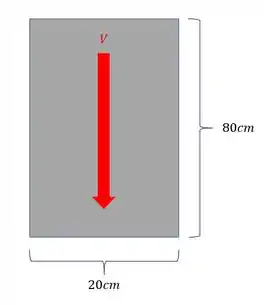
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata do cortante).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
Passo 2
Precisamos determinar primeiramente a linha neutra na nossa seção. A linha neutra de uma seção retangular uniforme sempre fica no centro da nossa seção. Como queremos saber o máximo cortante que devemos aplicar precisamos usar o ponto que há o maior cisalhante na nossa peça, e nesse caso o ponto com maior tensão cisalhante é o ponto sobre a linha neutra.
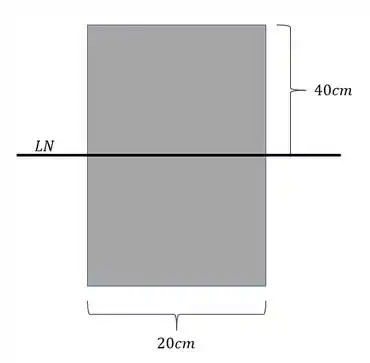
Passo 3
Precisamos definir agora o valor do nosso momento de inércia. Como a nossa seção é retangular sabemos que o momento de inercia será
Em que
Passo 4
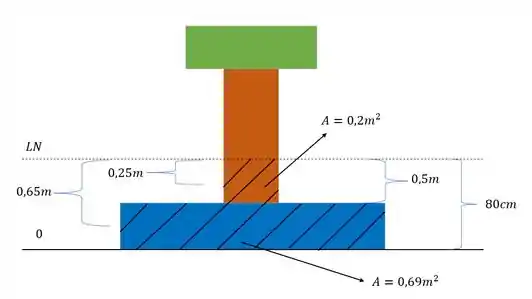
Agora vamos determinar o momento estático da nossa seção. Como no enunciado foi pedido o valor do cisalhante máximo, devemos fazer o cálculo levando em consideração as fibras da seção que contem a linha neutra, dessa forma também descobrimos que o valor da espessura de fibras usada no nosso cálculo será
Mas também queremos determinar o momento estático, nesse caso devemos escolher a seção acima da linha neutra ou abaixo da linha neutra. Analisando a nossa seção, faremos isso para a seção acima da linha neutra como mostra a figura
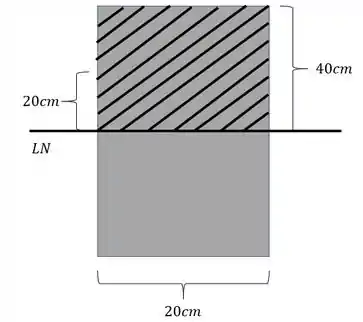
A fórmula do momento estático é dada por
Em que
Com isso teremos que
Passo 5
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que
Resposta
Exercício Resolvido #10
Elaboração própria
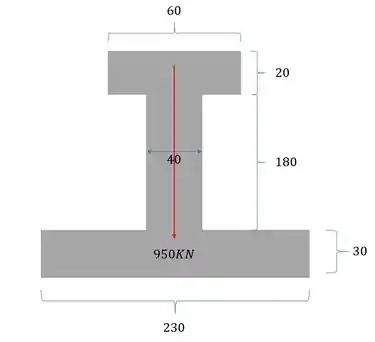
Uma estrutura de madeira com perfil T mostrado baixo é submetida a ação de um cortante de intensidade V. Sabendo que a resistência dessa madeira ao cisalhamento é de , determine o máximo cortante que podemos aplicar nessa peça sem que ela sofra um rompimento.
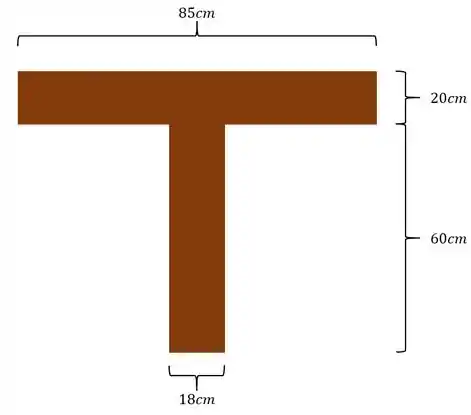
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata do cortante).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
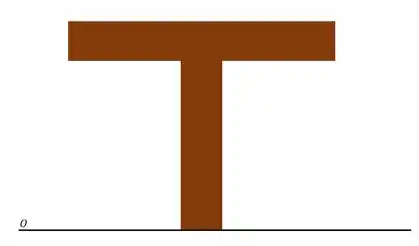
Passo 2
Precisamos determinar primeiramente a linha neutra na nossa seção. Sabemos que para determinarmos a linha neutra precisamos primeiro definir uma linha de origem, que geralmente passamos pela base da nossa seção.
Em seguida dividimos a nossa seção em figuras mais simples
Agora vem a parte legal, para cada uma dessas seções mais simples calculamos o valor da área e a distância do centroide de cada uma delas até a nossa linha de origem.

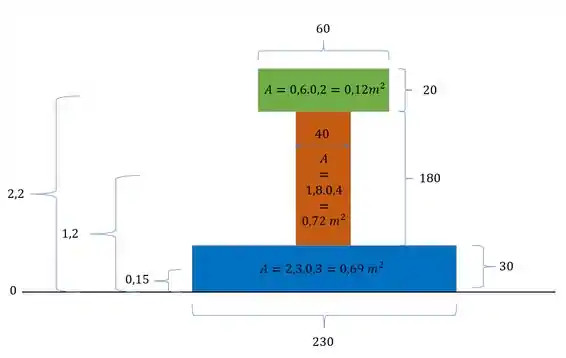
Agora para determinar a linha neutra basta usar a fórmula
Teremos que a linha neutra será marcada com relação a nossa origem

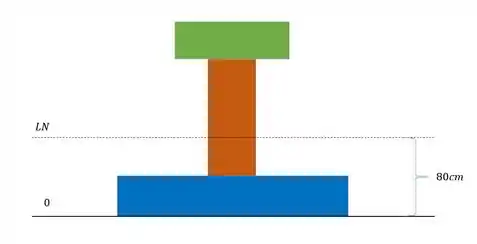
Passo 3
Precisamos definir agora o valor do nosso momento de inércia. Aqui devemos seguir um passo a passo como seguimos para determinação da linha neutra.
Vamos utilizar a mesma separação de figuras mais simples que usamos para determinação da linha neutra
Já sabemos quanto valem as áreas de cada seção, mas agora devemos calcular dois valores importantes. Primeiro o momento de inercia de cada uma das peças mais simples. Depois a distância do centroide de cada peça até a linha neutra. Na figura abaixo já verificamos tanto as áreas quanto as distâncias dos centroides até a linha neutra.
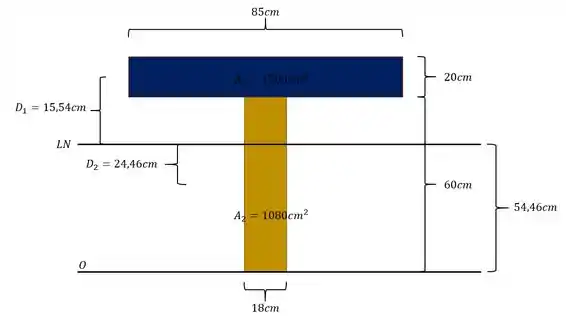
Vamos agora determinar o valor do momento de inercia para cada uma das peças. Sabemos que como todas são retângulos, a fórmula será
Olhando novamente as medidas teremos que
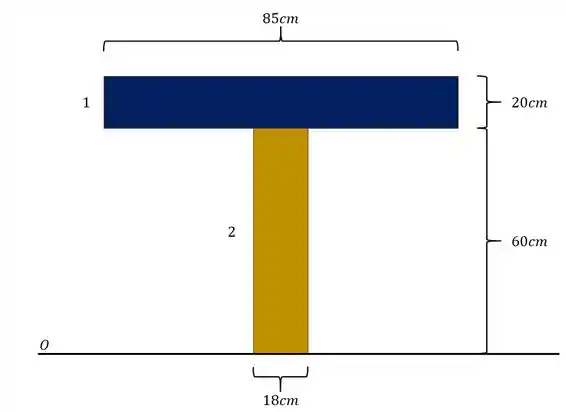
Logo
Com todos esses valores devemos usar a seguinte fórmula para determinarmos o momento de inercia da nossa seção
Substituindo nossos valores teremos que
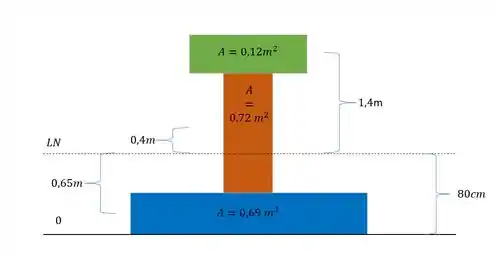
Passo 4
Agora vamos determinar o momento estático da nossa seção. Como no enunciado foi pedido o valor do cisalhante máximo, devemos fazer o cálculo levando em consideração as fibras da seção que contem a linha neutra, nesse caso a seção 2, dessa forma também descobrimos que o valor da espessura de fibras usada no nosso cálculo será
Mas também queremos determinar o momento estático, nesse caso devemos escolher a seção acima da linha neutra ou abaixo da linha neutra. Analisando a nossa seção, me parece mais simples fazer a conta analisando a parte de baixo da nossa seção, nesse caso pela nossa figura a nossa seção analisada será
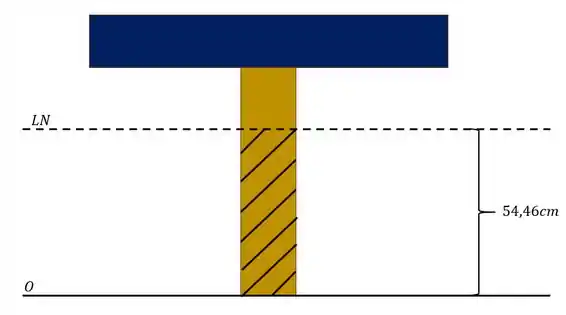
Agora precisamos saber o que fazer com essa seção, a fórmula do momento estático é dada por
Em que é a área da seção abaixo da linha neutra e a distancia do centroide dessa seção abaixo da linha neutra até a própria linha neutra. No esquema abaixo descobrimos que esses valores são os da figura
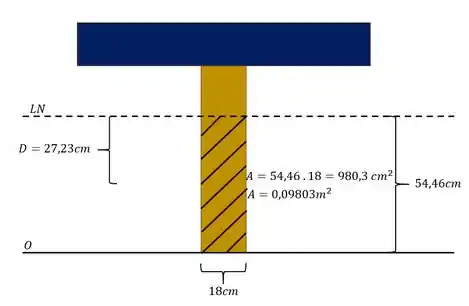
Agora basta substituir na fórmula os valores encontrados
Passo 5
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que