Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 114

114- A haste dobrada é sustentada por mancais em e e pelo arame . Sabendo que a porção da haste tem de comprimento, determine a tração no arame , as reações em e . Considere que o mancal em não exerce qualquer esforço axial.

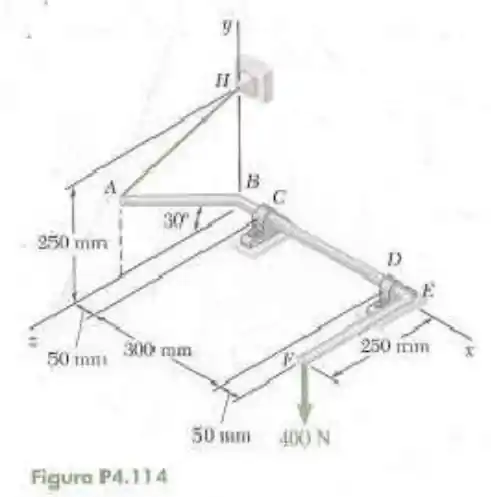
Passo 1

Os mancais C e D somente reações as forças e em todos os sentidos (bem como dito no enunciado diz que , ou a força axial em é nula). Além de reações a momentos em e (no caso positivas). E vamos nomear elas como:

Porém nessa questão vamos considerar que não há momentos sendo aplicados nos mancais.

E sabendo que a força no cabo vai de até teremos a seguinte representação da força:

Convertendo as medidas para metros e rebatendo a barra para e para .

Passo 2

Agora podemos encontrar a força no cabo fazendo a somatória dos momentos no eixo .

Onde na matriz dos momentos de teremos que colocar as distâncias que as forças podem ter para gerar momento no eixo . (Considerando a força saindo em )

Resolvendo os determinantes temos:

Passo 3

Agora vamos fazer a somatória dos momentos em para achar as forças em (lembrando que elas são positivas em e e nula em )

Onde a segunda linha é a distância relativa de até o ponto de aplicação da força. E a primeira matriz é o momento da força de apontada para baixo, a segunda o momento da força no cabo e a terceira matriz o momento do mancal .