Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 66
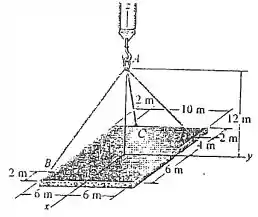
As extremidades dos três cabos estão presas a um anel em A e à borda da placa uniforme. Determine a maior massa que a placa pode ter se cada cabo pode suportar uma tração máxima de .
Passo 1
Fala meu querido!
Para encontrar a maior massa, podemos usar as equações de equilíbrio. Mas como a gente está no 3D, vamos precisar levar em consideração os 3 eixos coordenados.
Assim, a placa exerce uma força peso para baixo que pode ser chamada de W e é a mesma que os cabos puxam para cima a partir do ponto A.
Logo, fazendo o diagrama de corpo livre tem-se:
E, então, observando o desenho feito consegue-se montar as equações de equilíbrio.
Bora!
Passo 2
Precisamos das componentes das forças que estão atuando no eixo . A melhor forma de fazer isso aqui é achando a forma vetorial das nossas forças. O peso fica:
A gente chama de , porque não sabe seu valor.
Também é possível denotar as forças , e na forma vetorial. Multiplicamos o módulo delas por um vetor unitário na direção e sentido da força. Para achar o vetor a gente vai fazer coordenada final menos inicial de um segmento que está na direção do vetor.
Para ele ser unitário, o dividimos pelo módulo. Então, tem-se que
Para :
E para :
Passo 3
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Podemos escrever isso pela forma vetorial:
Essa relação nos dá as 3 equações de equilíbrio. Para acha-las, é avaliar o somatório de valores para cada componente dos vetores.
Olhando para cada componente dos vetores dessa relação separadamente, conseguimos montar as equações de equilíbrio. Olhando para a coordenada :
Passo 4
A partir das equações (1) e (2) é possível obter relações entre as forças, tal que:
Como a tração máxima permitida em cada cabo é de , então .
Logo, com esse valor das forças e a equação (3), é possível determinar a maior massa da placa:
Logo,