Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 120
120- Cada uma das estruturas mostradas nas figuras consiste em dois elementos em forma de ligados por duas hastes rígidas. Para cada estrutura, determine as reações nos apoios e indique se a estrutura é rígida.
Passo 1
Expondo as forças na letra nós temos:
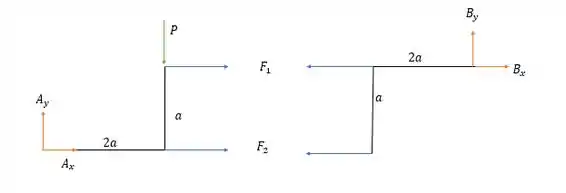
Na estrutura a esquerda dos cabos nós teremos a seguinte somatória dos momentos em .
E pela somatória das forças horizontais
E pela somatória das forças verticais:
Agora vamos para a estrutura a direita.
Fazendo a somatória dos momentos em .
Logo
E pela somatória das forças verticais temos:
E pela somatória das forças horizontais:
Todas as forças se equilibram, logo a estrutura é rígida.
Passo 2
Agora para a letra .
A somatória dos momentos em nos dá:
Pois gera momento em na vertical e na horizontal.
Agora fazendo a somatória dos momentos em pela estrutura a direita.
Substituindo isso na primeira equação nós teremos:
O que não é uma condição válida pois . Logo a estrutura é instável ou não rígida. O que faz com que não consigamos calcular as forças nos apoios.
Passo 3
Agora para a letra .
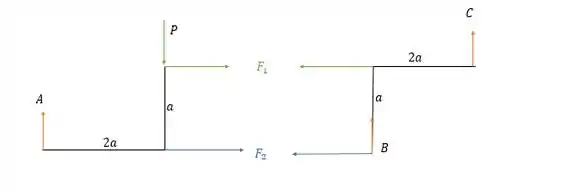
Note que os apoios são todos de primeiro grau agora .
Pela somatória dos momentos em na estrutura da esquerda temos:
Pela somatória das forças verticais
E pela somatória das forças horizontais:
Então na estrutura da direita se tem a seguinte somatória dos momentos em .
Logo valerá pela somatória das forças verticais:
Tudo equilibrado como deveria ser. Estrutura rígida.