Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 65
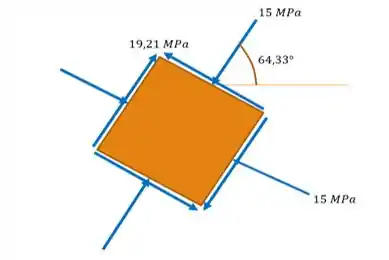
65. Resolva o Problema 9.15 usando o círculo de Mohr.
Passo 1
Da figura do enunciado, tiramos que:
Para construir o nosso famoso Círculo de Mohr a primeira coisa que temos que fazer é determinar o centro do círculo, que será dado através da fórmula da tensão média abaixo:
E substituindo os valores numéricos correspondentes, chegamos à:
Depois, a próxima coisa que temos que fazer é achar o raio do círculo através da fórmula da tensão máxima de cisalhamento , que é dada por:
Trocando os valores de cada variável, obtemos nosso raio como:
Passo 2
(a) Obtido o raio e o centro, já podemos construir o nosso círculo, que vai ter a seguinte cara:
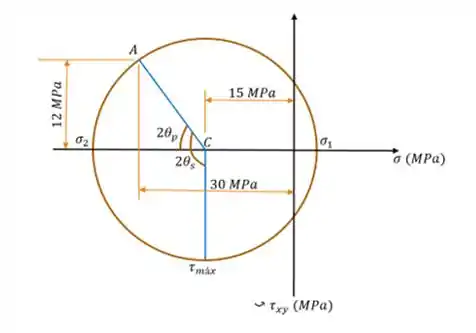
O próximo passo agora, é determinar o nosso ângulo , pertinente ao estado plano de tensão, que se for olhar bem o círculo, é dado por:
E o nosso primeiro ângulo de estado plano que é igual a é dado por:
E o sentido? Ora bolas você provavelmente chutaria anti-horário por causa do valor positivo. Mas aí erraria feio. Porque no calculo da tangente, ignoramos que a tensão de cisalhamento do nosso elemento, na verdade é negativa, já que só pegamos valores absolutos. Ou seja, nosso ângulo, na verdade está no sentido horário.
Vaamos então tratar de encontrar as tensões máxima e mínima , que de acordo com a figura, tiramos que são iguais a:
E assim, já podemos fazer um esboço do nosso elemento, que vai ter a seguinte tela:
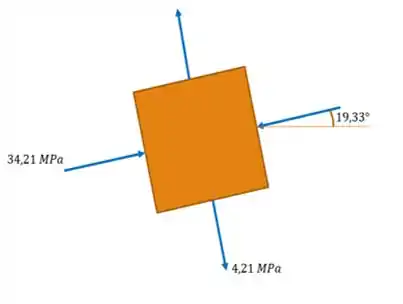
Passo 3
(b) Esse item é uma gracinha porque curiosamente, já respondemos ele praticamente inteiro no , quando estávamos coletando dados para fazer nosso círculo. Mas vejam só senhores!
A tensão de cisalhamento máximo que a questão pede, nada mais é do que o raio do nosso círculo e a tensão normal média é o centro do nosso círculo. Logo, de acordo com o que fizemos no , chegamos que:
Falta só calcular o nosso ângulo cisalhante , que se for novamente parar para observar o nosso maravilhoso círculo de Mohr, é dado por:
E o nosso primeiro ângulo cisalhante , que é igual a fica com o seguinte valor:
Esse ângulo agora sim, vai ficar no sentido anti-horário. É uma espécie de regra. Se ficou no sentido horário, então o ângulo cisalhante vai ficar no sentido oposto, ou seja anti-horário.
Só que vamos fazer algo diferente dessa vez. Bora tratar de esboçar nosso elemento em relação ao outro ângulo cisalhante , que é nada mais nada menos que o complemento de , em relação ao sentido horário:
Tá quase acabando! Só nos resta agora, esboçar o elemento cisalhante:
Resposta
(a)
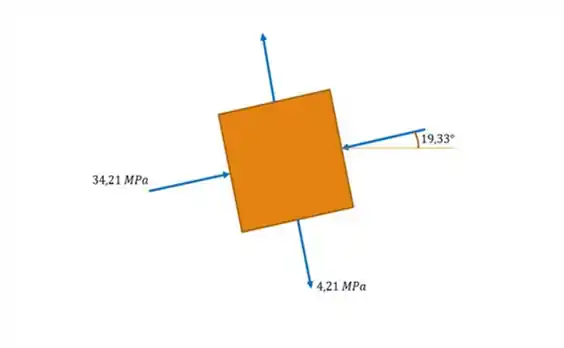
(b)
