Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 67

67. Determine os momentos de inércia I u e I v da área sombreada.

Passo 1

Opaaa.. belezinha??

Nessa questão vamos usar o momento de inércia pra retangular:

I = 1 12 b h 3

O teorema dos eixos paralelos:

I x = I - x ' + A d y 2

I x = I - y ' + A d y 2  

E as equações pros eixos inclinados.

I u = I x + I y 2 + I x - I y 2 cos ⁡ 2 θ - I x y sen ⁡ 2 θ

I v = I x + I y 2 - I x - I y 2 cos ⁡ 2 θ + I x y sen ⁡ 2 θ

Passo 2

Vamos separar a viga em duas partes:

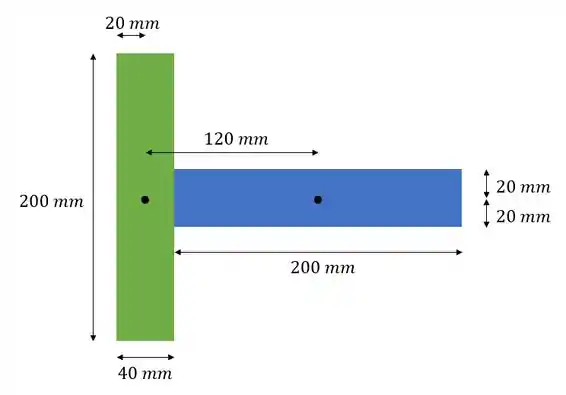
Calculando o momento de inércia em relação a x :

I x = 1 12 40 200 3 + 1 12 200 40 3 + 40 200 0

I x = 27,8 × 10 6   m m 4

Em relação a y :

I y = 1 12 200 40 3 + 1 12 40 200 3 + 40 200 120 2

I y = 1 42,9 × 10 6   m m 4

E como os centros das duas figuras estão alinhados, então:

I x y = 0

Passo 3

Agora só jogar nas equações:

I u = I x + I y 2 + I x - I y 2 cos ⁡ 2 θ - I x y sen ⁡ 2 θ

I u = I x + I y 2 + I x - I y 2 cos ⁡ 2 45 - I x y sen ⁡ 2 45

I u = 27,8 × 10 6 + 142,9 × 10 6 2 + 27,8 × 10 6 - 142,9 × 10 6 2 0 - 0 1

I u = 85,3 5 × 10 6   m m 4

I v = I x + I y 2 - I x - I y 2 cos ⁡ 2 θ + I x y sen ⁡ 2 θ

I v = 27,8 × 10 6 + 142,9 × 10 6 2 - 27,8 × 10 6 - 142,9 × 10 6 2 0 + 0 1

I v = 85,35 × 10 6   m m 4

Resposta

I u = 85,3 5 × 10 6   m m 4

I v = 85,3 5 × 10 6   m m 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O momento de inércia polar em relação ao eixo z ' passando pelo centroide C da área é J C = 64210 6m m 4 . O momento de inércia em relação ao eixo y ' é 264 10 6 m m 4 , e o momento de inércia em rela
Determine o momento de inercia em relação ao eixo x .
Determine a localização y ¯ do centroide da área da seção transversal do canal e depois calcule o momento de inércia da área em relação a esse eixo.
Determine y ¯ , que localize o eixo centroidal x ’ da área da seção transversal da viga T , e depois determine os momentos de inércia I x ' e I y ' .
Determine o momento de inércia da área da seção transversal da viga em relação ao eixo y .