91- Uma placa de madeira compensada de , pesando , foi temporariamente colocada entre três apoios tubulares. A borda inferior da placa apoia em pequenos cursores em e , e a borda superior está inclinada contra o tubo . Desprezando o atrito em toda a superfície, determine as reações em , e .
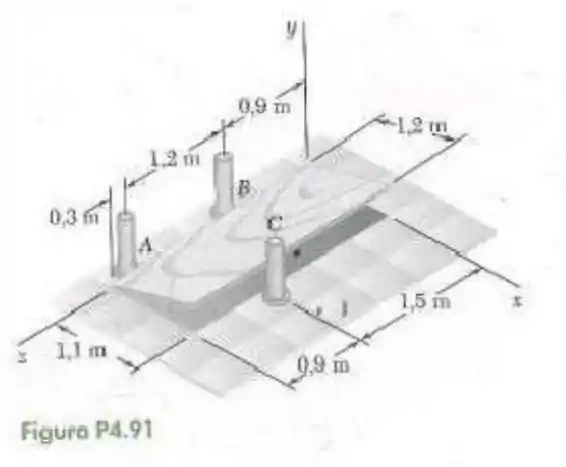
Passo 1
Primeiramente vamos calcular a altura que a placa atinge na sus extremidade, quando e a hipotenusa é de .
Isso será importante para nos dizer a posição onde encontra-se a posição da força peso da placa que encontra-se na metade da placa, ou seja em:
Passo 2
Considerando que e exercem reações positivas em e em e que exercia uma reação positiva em (porém desconsiderando o atrito será zero)e negativa em nós teremos então a seguinte somatória de momentos em .
Uma vez que as distâncias relativas de até e são:
Fazendo a determinante dessas matrizes nós temos:
Dessa forma juntando os termos que tem nós teremos:
Juntando os que tem :
E juntando os termos que tem :
Dessa forma as reações em e serão:
Passo 3
Agora vamos fazer a somatória de todas as forças e igualar a zero para poder encontrar a reação em :
Isso será:
Juntando os componentes que tem nós temos:
E os que tem :
Ou seja a reação em de forma vetorial fica: