Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 114

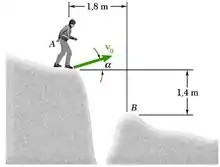
Um alpinista planeja pular de A para B sobre uma fenda. Determine o menor valor da velocidade inicial do alpinista v0 e o valor correspondente do ângulo α para que ele caia em B.

Passo 1

Primeira nota

v x 0 = v 0 cos ⁡ α

v y 0 = v 0 sin ⁡ α

Movimento horizontal. (Uniforme)

x = 0 + v x 0 t = v 0 cos ⁡ α t

No Ponto B:

1.8 = v 0 cos ⁡ α t

ou

t B = 1.8 v 0 cos ⁡ α

Passo 2

Movimento vertical. (Movimento uniformemente acelerado)

y = 0 + v y 0 t - 1 2 g t 2 = v 0 sin ⁡ α t - 1 2 g t 2               g = 9.81   m/ s 2

Passo 3

No Ponto B:

- 1.4 = v 0 sin ⁡ α t B - 1 2 g t B 2

Substituindo tB

- 1.4 = v 0 sin ⁡ α 1.8 v 0 cos ⁡ α - 1 2 g 1.8 v 0 cos ⁡ α 2

v 0 2 = 1.62 g cos 2   α 1.8 tan ⁡ α + 1.4 = 1.62 g 0.9 sin ⁡ 2 α + 1.4   cos 2   α

Passo 4

Agora minimize v 0 2 em relação a α .

Nós temos

d v 0 2 d α = 1.62 g - 1.8 cos ⁡ 2 α - 2.8 cos ⁡ α sin ⁡ α 0.9 sin ⁡ 2 α + 1.4   cos 2   α 2 = 0

ou

1.8 cos ⁡ 2 α - 1.4 sin ⁡ 2 α = 0 u

tan ⁡ 2 α = 18 14

ou

α = 26.0625 °             e             α = 206.06 °

Finalmente,

v 0 2 = 1.62 × 9.81 cos 2   26.0625 ° 1.8 tan ⁡ 26.0625 ° + 1.4

Resposta

Rejeitando o segundo valor porque não é fisicamente possível, temos

α = 26.1 °

v 0 min = 2.94   m/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos estágios finais de um pouso na Lua, o módulo lunar desce sob retropropulsão de seu motor de descida até h = 5m da superfície lunar onde tem uma velocidade para baixo de 2m / s . Se o motor de desc
O carro está viajando com uma velocidade constante v 0 = 100k m / h na parte horizontal da estrada. Quando o plano inclinado a 6 %( tan ⁡ θ = 6 / 100 ) é encontrado, o condutor não altera a posição do
Uma menina rola uma bola para cima em um plano inclinado e deixa esta retornar para ela. Para o ângulo θ e a bola em questão, a aceleração da bola ao longo da inclinação é constante em 0,25 g , dirigi
Uma força de desaceleração atua sobre uma partícula que inicialmente se desloca com uma velocidade de 100m / s e fornece uma desaceleração como a registrada pela leitura do osciloscópio mostrado na fi
Uma partícula viajando em uma linha reta encontra uma força que a retarda e provoca a redução de sua velocidade segundo v = 20 e - t / 10m / s , onde t é o tempo em segundos durante o qual a força age