Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 91

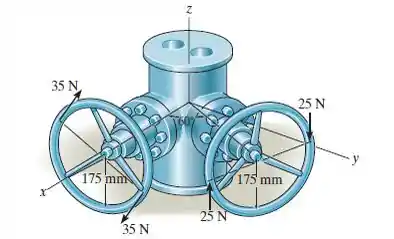
Um binário atua sobre cada um dos manípulos da válvula minidual. Determine a intensidade e os ângulos diretores coordenados do momento de binário resultante.

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Precisamos determinar a intensidade do momento de binário resultante e especificar os ângulos com os eixos coordenados.

A chave para resolvermos esta questão é escrever os momentos na forma vetorial. Ao obtermos ambas na forma vetorial, podemos somar ambas e obter as informações que a questão nos pede!

Passo 2

Começamos o nosso cálculo para o momento gerado pela força de 35   N é fácil. Como a distância é d = 2 ⋅ 0,175 = 0,35   m . O momento será:

M 1 = F d u 1

M 1 = - 35 ⋅ 0,35 i →

M 1 = - 12,25   i →   N ⋅ m

Muito cuidado na direção do momento! Percebam que pela regra da mão direita, ele está no sentido negativo do eixo x .

Passo 3

Já para o momento gerado pelo outro par de forças, temos:

M 2 = F d u 2

M 2 = - 25 ⋅ 0,35 u 2

O problema aqui é quem é a direção u 2 . Está é a direção do eixo sobre o qual temos o momento do binário. É uma direção que forma o ângulo de 60° com a direção positiva do eixo x .

Para podermos seguir o cálculo, temos que escrever o vetor unitário na direção u 2 . Ele será:

u 2 = cos ⁡ 60 ° i → + sen ⁡ 60 ° j →

Portanto, o momento M 2 é:

M 2 = - 8,75 cos ⁡ 60 ° i → + sen ⁡ 60 ° j →   N ⋅ m

M 2 = - 4,38   i → - 7,58   j →   N ⋅ m

Novamente, muito cuidado com o sinal do M 2 . Percebam que ele está no sentido negativo do eixo u 2 .

Passo 4

Agora que já temos ambos os momentos M 1 e M 2 na forma vetorial, podemos somar os dois. Desta forma, temos o seguinte momento resultante:

M r = M 1 + M 2

M r = - 16,63 i → - 7,58 j →   N ⋅ m

E a sua intensidade é:

M r = - 16,63 2 + - 7,58 2 = 18,3   N ⋅ m

Passo 5

Para finalizarmos a questão, basta calcularmos os ângulos formados com os eixos coordenados. Eles são os ângulos α , β e γ formados com a direção positiva dos eixos x , y e z , respectivamente.

Para calcularmos, temos:

α = arccos ⁡ M x M r = arccos ⁡ - 16,63 18,3 = 155 °

β = arccos ⁡ M y M r = arccos ⁡ - 7,58 18,3 = 114 °

γ = arccos ⁡ M z M r = arccos ⁡ 0 18,3 = 90 °

E assim finalizamos a questão!

Resposta

M r = 18,3   N ⋅ m

α = 155 °

β = 114 °

γ   = 90 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O lustre é sustentado por três corrente que são concorrentes no ponto O . Se a força em cada corrente possui uma intensidade de 300 N , expresse cada força como um vetor cartesiano e determine a inten
O lustre é sustentado por três correntes que são concorrentes no ponto O . Se a força resultante em O possui uma intensidade de 650N e é direcionada ao longo do eixo z positivo, determine a força em c
A torre de antena é sustentada por três cabos. Se as forças desses cabos que atuam sobre a antena são F B = 520 N, F C = 680 N e F D = 560 N, determine a intensidade e os ângulos de direção coordenado
O cabo A O exerce uma força sobre o topo do poste de F = { - 120 i - 90 j - 80 k } N. Se o cabo possui um comprimento de 1,02 m, determine a altura z do poste e a posição ( x ,y ) de sua base.
Se a resultante das quatro forças é F R = - 1,8 k kN, determine a tração desenvolvida em cada cabo. Devido à simetria a tração nos quatro cabos é a mesma.