Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 96
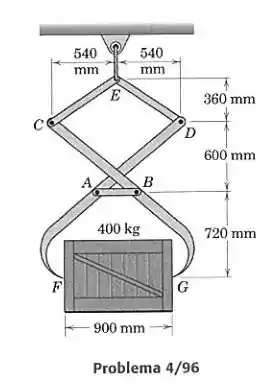
Calcule a força na conexão das garras de elevação que se cruzam sem se tocar.
Passo 1
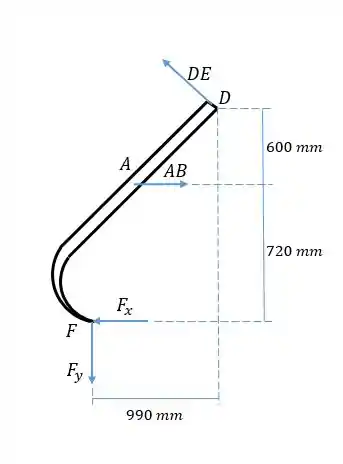
Vamos isolar em diagrama de corpo livre a garra , para aplicar a ela as condições de equilíbrio:
Passo 2
Como as duas garras devem segurar a caixa de 900 kg, pela simetria a força vertical aplicada por cada uma na ponta deve ser igual e a soma das duas deve ser igual ao peso da caixa, então calculamos da seguinte maneira:
Agora olhando para a figura vemos que só existe uma outra força vertical, que é a componente da fora , então devemos conseguir achar fazendo a soma das forças verticais ser zero.
Passo 3
Precisamos do ângulo que faz com a horizontal. A figura do enunciado nos dá as distâncias horizontal e vertical de a , iguais a 540 mm e 360 mm, respectivamente, então calculamos :
Agora fazendo a soma das forças verticais achamos :
Passo 4
Agora que temos o valor de , podemos fazer o momento em torno de (para evitar a força desconhecida):
Isolamos e substituímos o valor de pra chegar ao resultado:
Se g = 9,81 m/s²:
Como obtivemos valor positivo, a força em é de tração (estica a barra ) como desenhamos.