Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 122
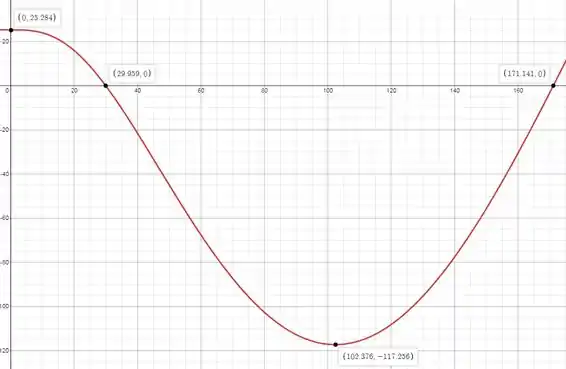
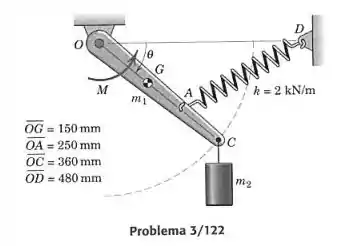
O centro de massa do braço de 10 kg está localizado em e a mola com constante não está esticada quando . Faça um gráfico do momento aplicado necessário para o equilíbrio estático na faixa . Determine o valor de para o qual (se existir) e os valores mínimo e máximo de , com os valores correspondentes de para os quais esses valores extremos ocorrem. O movimento desse mecanismo ocorre em um plano vertical. Considere positivo no sentido contrário aos ponteiros do relógio. O valor de é 3 kg.
Passo 1
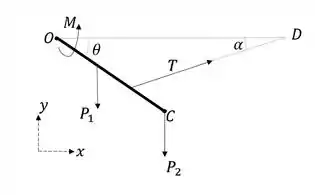
O que temos que fazer é satisfazer a equação de equilíbrio para momento em torno de atuando no braço . Isolando o braço num diagrama de corpo livre, temos o seguinte:
Precisamos da expressão da força elástica em função do ângulo e após isso fazemos a equação de equilíbrio.
Passo 2
O módulo da força eslástica é função da deformação da mola. Se a mola não esta esticada para , o tamanho da mola é :
O tamanho da mola esticada será o tamanho do vetor , então devemos achar esse vetor e então encontrar o módulo. Olhando o desenho e com os tamanhos dados no enunciado, temos:
Então fazemos o vetor e seu módulo :
Vamos calcular o módulo do vetor:
O módulo da força elástica pode então ser calculado:
Passo 3
Agora que temos o módulo da força, podemos calcular o vetor. A direção é a mesma de , então temos:
Onde é o vetor unitário na direção . Calculamos agora esse vetor unitário:
Então:
Passo 4
Agora calculamos as forças devidas ao peso do braço em e do peso de 3 kg em :
Pronto, agora já temos todas as forças, basta fazermos o equilíbrio do momento em torno de ser igual a zero para conseguirmos achar .
Passo 5
Calculamos agora o momento causado por cada força em torno de . Para e , que são verticais, apenas multiplicamos o módulo das forças pelo braço de alavanca (no caso a distância no eixo entre a aplicação da força e ).
Os valores são negativos pois os momentos aplicados são no sentido horário. Agora para atração , calculamos o momento pelo produto vetorial:
O vetor é simplesmente o vetor posição de e já foi calculado:
Agora podemos fazer o cálculo de . Vamos escrever como para facilitar as contas:
Agora, resolvendo o determinante:
Então:
Passo 6
Já temos todos os momentos em torno de . Agora basta resolvermos nossa equação de equilíbrio:
Passo 7
O seguinte gráfico mostra em função do ângulo , em graus, tal como o valor mínimo, o valor máximo, e os valores de para os quais :
