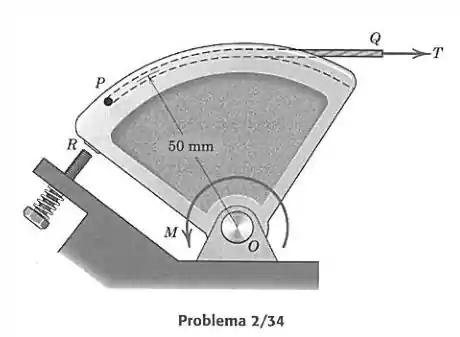
O componente de controle do acelerador pivota livremente em . Se uma mola de torção interna exerce um momento de retorno sobre o componente, quando ele está na posição mostrada, determine, para a finalidade do projeto, a força trativa necessária no cabo do acelerador para que o momento resultante em torno de seja zero. Observe que quando é zero, o componente se apoia no parafuso de ajuste de marcha lenta em .
Passo 1
Queremos que o momento em torno do ponto seja zero. Na posição mostrada, só atuam no componente o momento no sentido anti-horário e a força trativa , que causa um momento no sentido horário. Usando a convenção de que um momento anti-horário é positivo e um momento horário é negativo, a equação que temos é então:
Sendo o módulo do momento causado pela tração. Disso tiramos que
Passo 2
O momento causado por uma força em um ponto é o valor da força vezes o braço de alavanca, que é a distância entre a linha de ação da força e o ponto . A distância entre a linha horizontal de aplicação da tração e é de (não podemos esquecer de colocar as distâncias na unidade correta!)
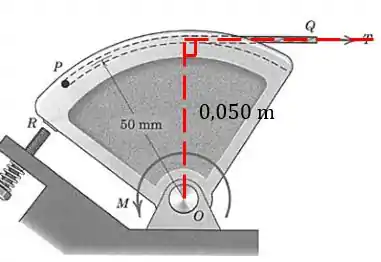
Então achamos a força :