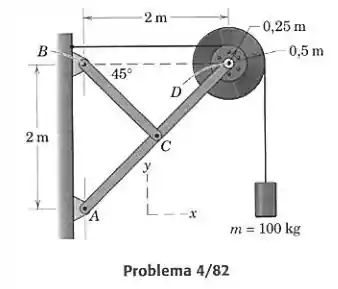
Determine as componentes x e y da força C , que o elemento B C exerce sobre o elemento A C D . Os cabos são enrolados firmemente em torno das duas polias, que estão aparafusadas entre si.

C x = 100 g( p a r aad i r e i t a ) C y = 100 g( p a r ab a i x o )

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 82

Determine as componentes e da força , que o elemento exerce sobre o elemento . Os cabos são enrolados firmemente em torno das duas polias, que estão aparafusadas entre si.

Passo 1

Queremos a força e pra isso precisamos aplicar equações de equilíbrio na barra . Porém antes disso temos que possuir o valor da força feita em . Então isolamos em diagrama de corpo livre a barra e as polias:

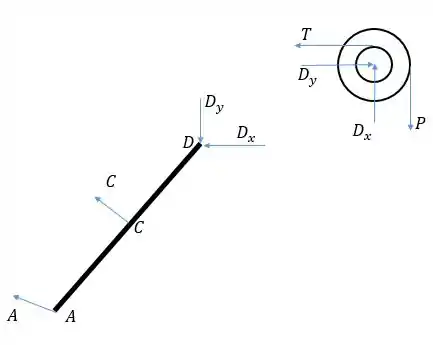
Passo 2

Vamos primeiro encontrar e através das equações de equilíbrio para a polia. O momento em torno do centro é zero, e os raios menor e maior são 0,25 m e 0,5 m. então:

A força sustenta a carga de 100 kg, então :

Agora pelos equilíbrios horizontal e vertical:

Passo 3

Agora vamos para a barra . Fazemos o momento em torno de , para evitar as forças desconhecidas daquele ponto. O ponto está no meio da barra. Então:

Substituindo o valor dos cossenos e das forças em , obtemos :

O valor negativo indica que o sentido é o contrário do que desenhamos. Então as componenetes são:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento da força F em relação ao ponto O. A força tem uma intensidade de800 N e ângulos diretores coordenados de α = 60 0 , β = 120 0 , γ = 45 0 . Expresse o resultado como um vetor cartes

Determine o momento da força F em relação ao ponto P. Expresse o resultado como um vetor cartesiano.Fonte: Estática Mecânica para Engenharia – 14ª ed

Determine o momento da força F = 600 N em relação ao ponto A.Fonte: Estática Mecânica para Engenharia – 14ª ed

A força F = {6i + 8j + 10k} N cria um momento em relação ao ponto O de M O = {-14i + 8j + 2k}N m. Se a força passa por um ponto tendo uma coordenada x de 1 m, determine as coordenadas y e z do ponto.

Determine a intensidade do momento da força F = 50 i - 20 j - 80 kN em relação à linha de base B C do tripé.