Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 67
Determine a força no elemento e as forças suportadas por todos os nós do suporte carregado.
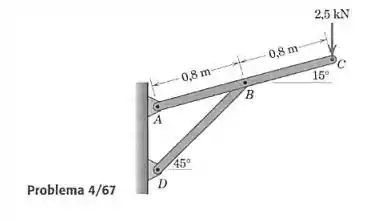
Passo 1
Vamos isolar o corpo num diagrama de corpo livre pra analisar as forças sobre ele:
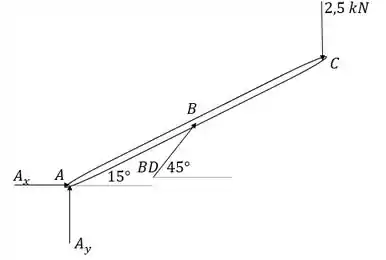
Vamos agora aplicas as equações de equilíbrio para esse corpo.
Passo 2
Como temos 2 forças desconhecidas em A, comoeçamos calculando o momento em torno desse ponto:
Aqui separamos em duas forças, uma horizontal que causa momento horário (negativo) e uma horizontal que causa momento anti-horário (positivo). Substituindo os valores dos senos e cossenos:
Passo 3
Então já temos as forças em e :
Agora devemos encontrar e para determinar a força em . Fazemos isso usando as somas das forças horizontas e verticais:
Substituindo pelo seno e o valor encontrado para :
O valor negativo diz que a força é para a esquerda e não para a direita. Agora para as forças verticais:
Substituindo os valores:
O valor negativo diz que a força é para baixo, e não para cima. Então obtemos a força em calculando o módulo: