Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 61
Determine as forças trativas nos cabos , e .
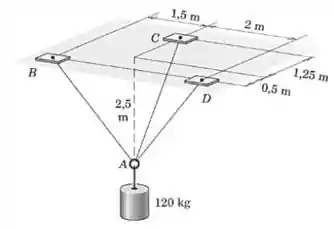
Passo 1
Vamos começar escrevendo vetores unitários nas direções de , , . Para isso precisamos definir um sistema de coordenadas:
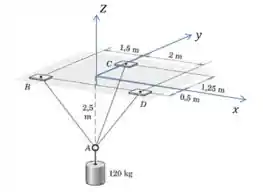
E podemos usar esses vetores unitários para definir os vetores das trações:
Passo 2
Agora precisamos escrever equações de equilíbrio para cada uma das componentes. Lembrando de acrescenter o peso na componente na direção :
Esse é um sistema bastante complicado, é uma boa ideia resover em forma matricial:
E agora você pode resolver isso usando qualquer método (eliminação de Gauss-Jordan por exemplo). Como esse não é um curso de álgebra matricial, o melhor a fazer é usar uma calculadora.
Nesse caso encontramos os seguintes resultados:
Resposta
Os módulos das forças são , e .
Exercícios de Livros Relacionados
Uma chapa quadrada e uniforme de aço com 360m m de comprimento de aresta e uma massa de 15k g está suspensa no plano horizontal pelos três fios verticais, como mostrado. Calcule a força trativa em cad
O eixo horizontal de aço tem uma massa de 480k g e está suspenso por um cabo vertical em A e por um segundo cabo B C que passa por baixo do eixo e está situado em um plano vertical transversal. Calcul
Duass vigas em I de aço, cada uma com uma massa de 100k g , estão soldadas em um ângulo reto e sustentadas por cabos verticais de forma que as vigas se mantêm em um plano horizontal. Calcule a força t
A parte de um lustre que é sustentada por correntes tem a forma de uma parte de casca esférica. Se a massa da parte de vidro é m , determina a força trativa T em cada uma das correntes.
A porta industrial de 600k g é um painel retangular uniforme que desliza ao longo do trilho fixo D , em roldanas presas a suportes em A e B . A porta é mantida em um plano vertical por uma roldana gui