Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 58

Determine o movimento horizontal do nó D se o comprimento do elemento BF é aumentado em 1.5 in.(Ver dica para o Problema 10.57.)

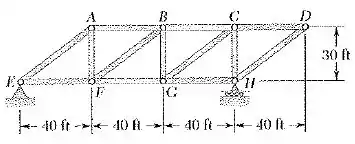
Passo 1

Primeiro vamos lembrar que, a soma dos momentos tem que ser igual a 0 e a soma das forças tem que ser igual a 0. Desse modo, no momento teremos:

∑ M H = 0

Então, note que:

P 3 0   f t - E y 120   f t = 0

Logo,

E y = P 4

De outra maneira temos:

∑ F y = 0

Então, note que:

3 5 F B F - P 4 = 0

Logo,

F B F = 5 12 P

Passo 2

Para o trabalho virtual, vamos primeiro remover o membro BF e substituir por suas forças F B F e - F B F , nos pinos F e B.

Então o trabalho virtual é dado por:

d U = 0

Implica que:

P d D + F B F d r F + - F B F d r B = 0

Portanto:

P d D + F B F ( d r B cos ⁡ θ B - d r F cos ⁡ θ F ) = 0

Observe que

d r B cos ⁡ θ B - d r F cos ⁡ θ F = d B F

Portanto:

P d D - F B F d B F = 0

Substituindo os valores que a questão nos oferece, teremos:

P d D - 5 12 P ( 1.5   i n ) = 0

Logo,

d D =   + 0 . 625   i n .

Resposta

d D =   + 0 . 625   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A posição da manivela ABC é controlada pelo cilindro hidráulico CD. Para o carregamento mostrado na figura, determine a força exercida pelo cilindro hidráulico no pino C quando θ = 55 ° .
A posição da manivela ABC é controlada pelo cilindro hidráulico CD. Determine o ângulo θ sabendo que o cilindro hidráulico exerce uma força de 15 k N no pino C.
O braço telescópico ABC é usado para prover uma plataforma elevada para operários construção. Juntos, operários e a plataforma têm um peso de 2250N , e seu centro de gravidade está localizado diretame
Resolva o problema 10.45 considerando que os operacios desceram para um ponto próximo ao solo de modo que θ = - 20 ° .
Voltando ao Problema 10.43 e usando o valor encontrado para a força exercida pelo cilindro hidráulico CD, determine a mudança no comprimento de CD necessária para se elevar a carga de 10kN em 15 mm.